Авторы: Dassault systems 

Источник: SolidWorks technical documentation 

COSMOSFloWorks моделирует движение потока, на основе решения уравнения Навье-стокса, которое являет интерпретацией законов сохранения массы, импульса и энергии для потока жидкости. Уравнения дополнены выражениями состояния жидкости, которые определяют природу жидкости и эмпирическими зависимостями плотности, вязкости и теплопроводности жидкости от температуры. Несжимаемые неньютоновские жидкости рассматриваются по зависимости их динамической вязкости от скорости деформации сдвига и температуры, а сжимаемые жидкости рассматриваются по зависимости их плотности от давления. Ещё одна часть уравнений отвечает за геометрию потока, граничные и начальные условия.   
  COSMOSFloWorks способна определять и ламинатрные и турбулентные течения Ламинарные течения возникают при низких значениях числа Рейнольдса, которое определяется как произведение величины скорости и линейного размера деленного на кинематическую вязкость. Когда число Рейнольдса превышает определённое критическое значение, поток становится турбулентным и его параметры начинают случайным образом подвергаться флоктации.    
   Большинство жидкостных течений, которые встречаются в инженерной практике турбулентные, поэтому COSMOSFloWorks в основном разрабатывалась для моделирования и изучения турбулентных потоков. Для расчёта турбулентных течений упомянутые уравнения Навье-Стокса усредняются по Рейнольдсу, т.е. используется осредненное по малому масштабу времени влияние турбулентности на параметры потока, а крупномасштабные временные изменения осреднённых по малому масштабц времени составляющих газодинамических параметров потока (давления, скоростей, температуры) учитываются введением соответствующих производных по времени. В результате уравнения имеют дополнительные члены - напряжения по Рейнольдсу, а для замыкания этой системы уравнений в COSMOSFloorks используются уравнения переноса кинетической энергии турбулентности и её диссипации в рамках k-e модели турбулентности.   
 COSMOSFloorks задействует одну систему уравнений для описания и ламинарных и турбулентных течений. Переход от ламинарного к турбулентному состоянию и наоборот также расчитываются. 
   Потоки в моделях с движущимися стенками (без изменения геометрии модели) рассчитываются путём спецификации соответствующих граничных условий. Потоки в модели с вращающимися частями рассчитываются в координатных системах закреплённых за вращающимися элементами модели т.е. вращаются вместе с ними. Т.е. стационарные части модели должны быть аксисимметричны к вращающейся оси. 
    Законы сохранения массы, импульса и энергии для потока жидкости в декартовой системе координат, которая вращается с угловой скоростью Ω вокруг оси, проходящей через начало системы координат можно записать следующим образом:

Где      u - скорость жидкости 
               p - плотность жидкости. 
               Si - внешние массовые силы, действующие на единицу массы текущей среды:
               Si=Si(porous) + Si(graviry) + Si(rotation)
               Si(porous) - сопротивление пористого тела; 
               Si(graviry) -сила гравитации; 
               Si(rotation)- центробежная сила 
               h- энтальпия 
               QH - источник тепла или тепло в единице объёма
               тik - тензор вязких сдвиговых напряжений 
               qi- тепловой поток за счёт диффузии 
    Нижние индексы отвечают проекциям на три координатные ветви. 

Для расчёта потоков с высоким числом Маха, доступна советующая опция и используется следующее уравнение: 

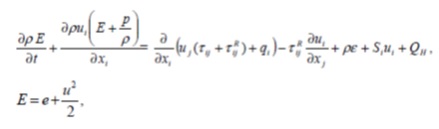
Где е – внутренняя энергия 

Для Ньютоновских жидкостей тензор вязких сдвиговых напряжений определяется как: 

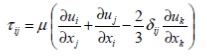
Согласно допущениям Буссинеска тензор по Рейнольдзу принимает следующую форму: 

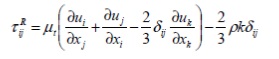
Где - дельта-функция Кронекера (равна 1 при і=j; 0 при і≠j) 

Сжимаемые жидкости 

Сжимаемые жидкости чья плотность зависит от температуры и давления могут быть рассчитаны на основе следующих приближений:
    - по логарифмической зависимости: 

где    р0 - плотность жидкости при давлении P0 
             С, В – коэффициенты 

- по степенной зависимости: 

где, кроме вышеупомянутых параметров, используется также n - параметр степени, который тоже может зависеть от температуры. 

Неньютоновские жидкости 

COSMOSFloorks может расчитывать ламинарные потоки несжимаемых неньютоновских жидкостей. В этом случае тензор вязких сдвиговых напряжений определяется вместо Eq, следующим образом: 

Где скорость сдвиговых деформаций:

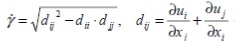
Для определения функции вязкости в COSMOSFloorks доступны следующие три модели: 
- Модель Herschel-Bulkley: 

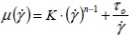
Где К – коэффициент консистенции жидкости, n – коэффициент степенного закона, τ0 – предельное сдвиговое напряжение. Эта модель имеет следующие частные случаи 
    - n=1, τ0=0 – неньютоновские жидкости, в этом случает К- динамическая вязкость жидкости; 
  - n=1, τ0>0 – неньютоновские жидкости, описываемые моделью Bingham, особенностью которой является ненулевая величина τ0=0: неньютоновская жидкость ведет себя как твёрдое тело при τ< τ0 (это изменение поведения жидкости моделируется тем, что при τ<τ0 коэффициент консистенсии К, который в этой модели называется пластичской вязкостью, автоматически становится достаточно большим): 
  - 0<n<1, τ0=0 – так называемые «утончающиеся» неньютоновские жидкости, поведение которых описывается степенным законом; 
    - n>1, τ0=0 – так называемые «утолщающиеся» неньютоновские жидкости поведение которых описывается степенным законом: 

- модель со степенным законом: 

В отличии от частного случая модели Hershel-Bulkley величина μ в этой модели ограничена μmin < μ< μmax, эти минимальная и максимальная динамическая вязкости задаются в дополнение к коэффициенту консистенсии К и коэффициенту степенного закона n; 

- модель Careau

Где μ∞ - динамическая вязкость жидкости при бесконечно большой скорости сдвиговой деформации, т.е. минимальная динамическая вязкость, μ0 – динамическая вязкость жидкости при нулевой скорости сдвиговой деформации, т.е. максимальная динамическая вязкость, Кt - временная постоянная, n – коэффициент степенного закона. Эта модель – вариант сглаживания модели со степенным законом с её ограничениями на величину μ. Все параметы этих моделей, за исключением n, в общем случае зависят от температуры.