Авторы: Гусак О.Г., Каплун І. П., Матвієнко О.А. 

Источник: Наукові праці Донецького національного технічного університету. Серія: гірничо-електромеханічна.- 2011.- Випуск 22(195).- C.73-85.

В статті аналізується можливість підвищення параметрів малогабаритного осьового ступеню свердловинного насосу за рахунок зміни осьового зазору між лопатевими гратками робочого колеса та статорного апарату. Дослідження проводилися за допомогою чисельного моделювання потоку в каналах проточної частини. Отримано напірні та енергетичні характеристики в залежності від довжини осьового зазору. 

Ключові слова: осьовий насос, артезіанське водопостачання, заглибні свердловинні насоси, чисельне моделювання, напірні характеристики, енергетичні характеристики. 

За даними європейської асоціації виробників насосного обладнання Europump насосними системами споживається приблизно 20% виробленої в світі електроенергії [1]. В рамках виконання директив Європарламенту Europump розпочала реалізацію програми під назвою Ecopump по зниженню споживання електроенергії насосним обладнання на 40% до 2020 року. Аналогічну програму розробляє і Російська асоціація виробників насосів (РАПН) [2]. В Україні програми у вказаному напрямку не існує. Крім того при виборі насосного обладнання українські користувачі, розглядаючи пропозиції-аналоги, найчастіше віддають перевагу варіантам з найменшою початковою ціною, практично не звертаючи уваги на вартість експлуатації. В той же час на думку авторів [3], вибір найкращого варіанту повинен проводитися з позицій мінімізації загальної величини затрат за весь період служби обладнання. Відомо [4], що, наприклад, при покупці свердловинного насосу споживач в середньому платить лише 5-8% від суми, яку він витрачає протягом усього строку експлуатації, в той час, як витрати на оплату спожитої електроенергії складають близько 80% вказаної суми. Очевидно, що в умовах постійного зростання цін на енергетичні ресурси та їх дефіциту, все більше уваги буде приділятися їх економному споживанню. Відповідно, висуватимуться нові вимоги і до рівня ККД насосів, в тому числі і свердловинних. Особливо гостро це питання постає при розробці нового обладнання. 

Проблема і її зв'язок з науковими і технічними задачами.

 Як зазначалося у попередніх роботах [5, 6], для мінімізації як капітальних так і експлуатаційних затрат система водозабезпечення із свердловин при заданій продуктивності повинна мати мінімальний діаметр свердловини (наскільки дозволяють місцеві геологічні умови при забезпеченні необхідного дебету) для зниження вартості її буріння та облаштування, а насосний агрегат у складі насосної установки повинен мати максимальний середньоексплуатаційний ККД для зниження вартості експлуатації. 
  Відповідно свердловинні насоси повинні мати максимально можливі подачі при мінімальних радіальних габаритах. Зауважимо, що більшість європейських фірм-виробників свердловинних насосів уже мають у складі лінійки насосних агрегатів, що виробляються, високовитратні насоси з діагональними ступенями та високим ККД, а резерви подальшого його підвищення в більшості випадків можна вважати практично вичерпаними. Створення насосів, спроможних з ними конкурувати в більшості випадків виглядає досить проблематичним, так як вимагає значних затрат без гарантії отримання кращого результату. 
   В таких умовах доцільним виглядає використання розроблених на кафедрі прикладної гідроаеромеханіки Сумського державного університету малогабаритних осьових ступенів низької швидкохідності [1, 6, 7], які в даному випадку мають ряд переваг. Як відомо, осьові проточні частини вирізняються високим значенням гідравлічного ККД (на рівні 87-90%). Також при високих подачах ступені такого типу забезпечують найбільш просту та компактну конструкцію, що особливо важливо в обмежених умовах свердловин. 
    Та, напевно, вирішальною перевагою осьових ступенів для свердловинних насосів є те, що вони дають можливість в 1,5 – 1,7 рази підвищити подачу у порівнянні з відцентровими ступенями при незмінних радіальних габаритах. 
    При створенні дослідного зразка осьового ступеню низької швидкохідності були розроблені робоче колесо (РК) та статорний апарат (СА). Тривимірна модель ступеню та дослідний зразок робочого колеса представлені на рис. 1 а та 1 б відповідно. Варто зазначити, що ступінь проектувався виходячи з вимог забезпечення максимально можливого напору. Для забезпечення високого ККД використовувалися просторові профільовані гратки лопатей. Їх проектування проводилося як з використанням уже відомих методик [7], так і з використанням експериментальних уточнюючих коефіцієнтів. 

а) б) Рис. 1. а) Тривимірна модель осьового малогабаритного ступеню свердловинного заглибного насосу, б) дослідний зразок осьового робочого колеса малогабаритного ступеню свердловинного заглибного насосу.

Незважаючи на отримані досить високі значення напору та ККД [1], на наш погляд, ступінь має ряд перспективних напрямків для йо- го подальшого вдосконалення. Один з них, а саме вплив осьового зазору на основні показники малогабаритного осьового ступеню, і є предметом розгляду в даній статті. 

Аналіз досліджень і публікацій. 

Одним з основних допущень при аналізі течії ідеальної рідини та розрахунку лопатевої машини, яке було обґрунтовано Ю.Г. Степановим [9], є те, що осереднений потік в міжлопатевому зазорі приймається вісесиметричним, а параметри потоку за лопатками не залежать від осьової координати. Однак, результати експериментальних даних багатьох авторів [9, 10, 11, 12] вказують на існування певного взаємного впливу двох лопатевих ґраток, одна з яких руха- ється по відношенню до іншої, а також на необхідність розташування їх на певній відстані одна від одної в осьовому напрямку, достатній для вирівнювання поля швидкостей за першою граткою. Неоднорідність потоку навколо лопатевої ґратки пояснюється [9] збуренням потенційного потоку та наявністю кромкового сліду. Відповідно, дані два фактори є першопричинами взаємного впливу ґраток. Збурення впотенційному потоці спостерігається як перед ґраткою, так і за нею. Очевидно, збурення буде викликати збурене обтікання двох сусідніх ґраток (на наступних гратках це збурення практично не буде відчуватися, так як воно затухає за експоненціальним законом). Кромковий слід поширюється вниз по потоку, тому він практично впливає лише на обтікання граток, які розміщені за збурюючою граткою. 
    Таким чином, можна зробити висновок, що осьовий зазор між лопатевими гратками необхідно збільшувати для зменшення впливу збурень потоку та кромкового сліду. З іншого боку збільшення осьового зазору лімітується втратами енергії на тертя рідини об поверхні, що обмежують проточну частину. Дані втрати прямо пропорційні довжині осьового зазору. Крім того збільшення зазору між лопатевими гратками призводить до погіршення масогабаритних показників насосу, що також небажано. Таким чином, вивчення взаємного впливу граток дозволить обрати оптимальний осьовий зазор між лопатевими системами при якому втрати енергії будуть мінімально можливими та масогабаритні показники матимуть прийнятні значення. 
   Незважаючи на велику різноманітність видів лопатевих машин та їх призначення, робочі процеси, які відбуваються у їх проточних частинах, мають багато спільних рис. Тому, на наш погляд, доцільно звернутися до досвіду, накопиченого з вказаного питання при розробці як компресорів та вентиляторів, так і турбін. 
   На думку автора [10] для газової реактивної турбіни взаємний вплив ґраток внаслідок збурень, які переміщуються в потенційному потоці, може бути досить значним. Зменшити цей ефект пропонується збільшенням осьового зазору між гратками. У роботі [10] приводиться графік залежності ККД турбіни від величини осьового зазору між рядами лопатевих граток, який підтверджує дану гіпотезу. 
    В роботі [11] зазначається, що при дуже малих осьових зазорах ефект потенційної взаємодії струмин проявляється найбільш сильно. Однак при поступовому збільшенні осьового зазору починає збільшуватися вплив ефектів в’язкості у потоці. Таким чином, було встановлено, що для деяких турбін може існувати оптимальна величина осьового зазору. Максимальне значення ККД буде отримано у тому випадку, коли осьовий зазор збільшується до значення, при якому збільшення втрат від взаємодії кромкових слідів перестає компенсуватися зниженням втрат від взаємодії в потенційному потоці. 

Рис. 2. а) Залежність максимального ККД турбіни від осьового зазору між рядами лопаток [10], б) Вплив осьового зазору на відносний ККД осьової турбіни [11] 

На рис. 2б [11] представлено графік залежності відносного значення ККД осьової турбіни від відносного осьового зазору. Як бачимо з графіка, у деяких досліджуваних турбін оптимальне значення ККД досягалося при осьових зазорах, які складали приблизно 15 % висоти робочих лопаток. На жаль, не було спроб використати довжину хорди профілю або ширину вузького перетину між лопатевого каналу у якості номінуючого параметру, що дозволило б отримати узагальнене емпіричне співвідношення. 
    У осьових компресорах, як зазначається у праці [11], зміна значення осьового зазору між лопатевими гратками ротора та статора багатоступеневої машини призводить до значної зміни його ККД та максимального ступеня підвищення тиску. Дані зміни на думку автора краще корелюють з величиною осьового зазору віднесеного до кроку гратки, ніж з віднесеною до хорди та тим паче до висоти лопасті. Все вищевказане свідчить про те, що ефекти взаємодії в потенційному потоці можуть значно впливати на характер течії в гратках. Вплив осьового зазору на ККД компресора проявляється наступним чином: максимальний ККД можна отримати в тому випадку, коли лопаті лопатевих систем встановлені якнайближче одна до одної, а при збільшенні осьового зазору ККД знижується. 
    Експериментальні дослідження [12] характеристик осьових вентиляторів показали, що в інтервалі осьових зазорів між лопатевими системами робочого колеса і статорного апарата в межах (0,25…0,5) хорди лопаті параметри машини практично не змінюються. Проте, при зближенні лопатевих граток до (0,1…0,2) довжини хорди ККД збільшується приблизно на 1%, а при збільшенні цих зазорів понад (0,5…0,7) ККД знижується на 1…1,5%. При цьому автор оперує значеннями довжин зазорів на середньому радіусі, віднесених до довжи- ни хорди лопасті робочого колеса. 
    За даними роботи [13] в осьових насосах довжину осьового зазору звичайно обирають в межах (0,15…0,25) довжини хорди профілю. При проектуванні осьових робочих коліс автор роботи [14] рекомендує приймати довжину осьового зазору рівним довжині основної ділянки гідродинамічного сліду (рис. 5): h = Xsinβ2 ≈ tsin2 β2 (1) де Х – довжина основної ділянки гідродинамічного сліду; β2 – кут на виході з лопасті; t – крок гратки. 

Рис. 3. Схема основної ділянки гідродинамічних слідів за граткою профілів робочого колеса [14]: 1 – закромковий слід (наслідок скінченої товщини вихідної кромки), 2 – основний потік, 3 – гідродинамічний слід; 4 – розподіл швидкостей у сліді, S – половина ширини гідродинамічного сліду. 

Зважаючи на наявність певних суперечностей між існуючими даними щодо величини оптимального осьового зазору між лопатями осьового робочого колеса та статорного апарату, а також їх частковість та недостатність для обґрунтованого вибору даного параметру для досліджуваних малогабаритних ступенів низької швидкохідності, було визнано доцільним виконати окреме дослідження. 

Викладення матеріалу та результати. 

Вказане дослідження проводилося за допомого чисельного моделювання в університетській версії програмного продукту ANSYS CFX. Для коректного моделювання умов роботи проміжного ступеню насосу використовувалась багатозв’язна розрахункова область, яка складалася з вхідного елемента, трьох робочих коліс та статорних апаратів, а також вихідного елементу. Всі результати були отримані для середнього з трьох ступенів. З метою економії ресурсів ЕОМ ви- користовувана геометрична модель становила лише частину повного об’єму рідини (рис. 5). 
    Дослідження проводилося в два етапи: перший – дослідження зазору між робочим колесом та статорним апаратом (S1 на рис. 4), другий – дослідження зазору між статорним апаратом та робочим колесом наступної ступені з урахуванням результатів отриманих на першому етапі (S2 на рис. 4). Моделювання проводилося для двох ти- порозмірів малогабаритних осьових ступенів – з коефіцієнтом подачі [15] відповідно KQ=0,185 та KQ=0,386.

Рис. 4. Схема досліджуваної проточної частини осьового насоса низької швидкохідності 

Розрахункова сітка (рис. 5) була створена у компоненті програмного комплексу ANSYS, і нараховувала приблизно 0,8 млн. призматичних комірок у робочому колесі та 0,6 млн. у статорному апараті. Для належного опису пограничних шарів поблизу твердих стінок гус- тину сітки було збільшено. Величина змінної Y+ знаходилася в межах від 10 до 100 одиниць, що відповідає рекомендаціям, приведеним в посібнику користувача [16]. 
   Розрахунок у вказаному програмному продукті виконувався шляхом чисельного розв’язання системи рівнянь (1), котрі описують найбільш загальний випадок руху рідкого середовища - рівнянь Нав'є-Стокса та нерозривності.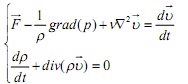 

Рис. 5. Приклад розрахункової сітки в робочому колесі 

Густина рідини при розрахунку була прийнятою за постійну величину. Моделювання турбулентних течій здійснювалося за допомогою системи рівнянь Рейнольдса, для замикання котрих використовувалася стандартна k-ε модель турбулентності. 
   На рис. 6 наведено отримані в результаті чисельного моделювання залежності значень напору ступеню від значення осьового зазору між лопатевими гратками для зазору до статорного апарату та після відповідно. Варто зазначити, що мінімальний зазор між лопатевими гратками робочого колеса і статорного апарату приймався рівним 4 мм з технологічних міркувань. 
   Для того, щоб охарактеризувати залежність напору та ККД ступеню від довжини осьового зазору між лопатевими гратками робочого колеса та статорного апарату S1 та S2 введемо поняття відносної довжини осьового зазору: Sі ’ = Sі/l де Si – довжина зазору між лопатевими гратками, мм l – довжина хорди лопаті на привтулковому перетині, мм. 
    Як бачимо, криві на рис. 6а мають чітко виражену область оптимальних значень, при чому у лівій частині графіка, яка передує оптимальній зоні, градієнт значень значно більший, що може вказувати на переважання втрат, які виникають в кромковому сліді. У правій частині графіка форма кривої більш полога, що ймовірно вказує на переважання втрат напору на тертя, які прямо пропорційні довжині осьового зазору, тобто у цій зоні переважають ефекти в’язкості.

Рис. 6. Залежності значень напору ступеню від значення осьового зазору між лопатевими гратками малогабаритного осьового ступеню низької швидкохідності а) між робочим колесом та статорним апаратом, б) між статорним апаратом та робочим колесом наступного ступеню 

Розглядаючи криві залежності напору ступені від довжини осьового зазору між лопатевими гратками статорного апарату та робочого колеса (S2), можна сказати, що характер кривих має дещо інший вигляд. На цих кривих чіткого оптимуму не спостерігається, крім того в робочому колесі із меншим коефіцієнтом подачі наявна зона западання в лівій частині.
  На рис. 7 наведено отримані в результаті чисельного моделювання залежності значень гідравлічного ККД ступеню від значень осьового зазору між лопатевими гратками для зазору до статорного апарату та після нього відповідно. 

Рис. 7. Результати чисельного моделювання залежності значень ККД ступеню від значення осьового зазору між лопатевими гратками малогабаритного осьового ступеню низької швидкохідності а) для зазору між робочим колесом та статорним апаратом, б) між статорним апаратом та робочим колесом наступної ступені 

Варто зазначити, що моделювання проводилося без урахування механічного ККД і його зміни в залежності від зміни значення довжини осьового зазору між лопатевими гратками проточної частини. Таке спрощення було введено через недостатність обчислювальних потужностей, так як при такій постановці задачі розрахункова область значно ускладнюється і потребує значно більших ресурсів ЕОМ. 
    Як бачимо з рис. 7 а та б криві залежності гідравлічного ККД від довжини осьового зазору мають чітко виражені зони оптимальних значень як у випадку зазору S1, так і для S2. 
    Порівняння отриманих оптимальних значень довжини осьового зазору наведені у табл. 2.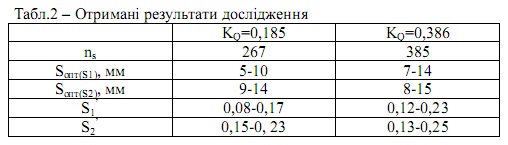 

Виходячи із отриманих результатів зазначимо, що оптимальні значення довжини осьового зазору між лопатевими гратками робочого колеса та статорного апарату S1 при різних значеннях коефіцієнта швидкохідності (в даному випадку 267 та 385) відрізняються приблизно на 30%, при цьому оптимальні значення довжини осьового зазору між лопатевими гратками статорного апарату та робочого колеса S2 майже не залежать від коефіцієнта швидкохідності ns та близькі за значенням. 
    Зауважимо, що наведені результати можливо розглядати як попередні і як основу для проведення подальших досліджень, у тому числі і для отримання залежності оптимальних параметрів осьового зазору від коефіцієнта швидкохідності та коефіцієнта реактивності малогабаритного осьового ступеню. 

Висновки. 

1. При збереженні сучасних тенденцій розвитку насособудування в області свердловинних насосів значні перспективи має створення осьових проточних частин наднизької швидкохідності, які мають високий гідравлічний ККД та можуть забезпечувати високі значення подач при мінімальних радіальних габаритах, що вкрай важливо для свердловин. 
2. В результаті проведення чисельного експерименту було встановлено, що ККД осьового малогабаритного ступеню суттєво залежить від довжини осьового зазору між лопатевими гратками проточної частини. Були отримані залежності напору та гідравлічного ККД ступеню в залежності від довжини осьового зазору як перед робочим колесом, так і за ним. 
3. Встановлено, що оптимальне значення осьового зазору між лопатевими гратками робочого колеса та статорного апарату залежать від коефіцієнту швидкохідності ступеню. 
4. Намічені шляхи щодо подальшого покращення його характеристик, які необхідно досліджувати в майбутньому. 

Список літератури 

1. Теория и практика насосо- и компрессоростроения: монография / А.Г. Гусак, О.А. Демче- нко, И.П. Каплун; под ред. В.А. Марцинковского, И.Б. Твердохлеба, Е.Н. Савченко // При- менение малогабаритных осевых ступеней низкой быстроходности в скважинных насосах для водоснабжения. – Сумы: Сумский государственный университет, 2011. – С. 300 – 309. 
2. Караханьян В. Энергосбережение и повышение энергоэффективности насосного оборудования в России в период до 2020 г. / В. Караханьян // Насосы и оборудование. – 2010. – №4-5. – С.4-6 
3. Твердохлеб И. О стоимости жизненного цикла насосов / И. Твердохлеб, А. Костюк // Насосы и оборудование. – 2010. – №3. – С. 26 – 28. 
4. A. Gusak Energy-efficient Borehole Pumps Based on Axial Stages of Low Specific Speed / A. Gusak, O. Demchenko, I. Kaplun // MOTROL 12d. – 2010. – Р. 45-54. 
5. Гусак О.Г. Перспективи використання осьових насосів для артезіанського водопостачання/ О.Г. Гусак, О.А. Демченко, І.П. Каплун // Промислова гідравліка і пневматика. – 2010 – №4(30). – С.8 – 12. 
6. Investigation of small-sized axial-flow stage of a borehole pump for water supply / A. Gusak, O. Demchenko, I. Kaplun; edited by: A.Gajic, M.Benisek, M.Nedeljkovic // Proceedings of the 4th international meeting on Cavitation and dynamic problems in hydraulic machinery and systems IAHR-WG 2011. – Belgrade: University of Belgrade, Faculty of Mechanical Engineering, 2011. – P.143 – 150 
7. Гусак О.Г. Порівняльний аналіз методик проектування протічних частин осьових насосів / О.Г. Гусак, О.А. Демченко, І.П. Каплун // Наукові праці ДонНТУ. Серія гірничо- електромеханічна. – 2011. – С. 44-58. 
8. Степанов Г.Ю. Гидродинамика решеток турбомашин / Г.Ю. Степанов. – М.: Государст- венное издательство физико-математической литературы, 1962. – 512 с. 
9. Самойлович Г.С. Возбуждение колебаний лопаток турбомашин / Г.С. Самойлович. – М.: Машиностроение, 1975. – 287 с. 
10. Аэродинамика турбин и компрессоров / под ред. У. Р. Хауторна; [пер. с англ. В.Л. Самсо- нова, В.С. Бекнева, О.Н. Самсонова]. – М.: Машиностроение, 1968. - 742 с. 
11. Гостелоу, Дж. Аэродинамика решеток турбомашин / Дж. Гостелоу ; [пер. с англ. Н.М. Савина, А.П. Кадетова]. – М.: Мир, 1987. -392 с. 
12. Брусиловский И.В. Аэродинамика осевых вентиляторов / И.В. Брусиловский. – М.: Машиностроение, 1984. – 239 с. 
13. Старицкий В.Г. К учету взаимодействия решеток рабочего колеса и направляющего аппарата в осевых гідромашинах / В.Г. Старицкий // Труды ленинградского политехнического института им. М.И. Калинина. – 1956 – №187 – С. 27-35. 
14. Лопастные насосы: справочник / В.А. Зимницкий, А.В. Каплун, А.Н. Папир, В.А. Умов; под ред. В.А. Зимницкого, В.А. Умова. – Л.: Машиностроение, 1986. – 334 с. 
15. Насосы осевые. Общие технические условия: ГОСТ 9366-80. – М.: Издательство стандартов, 1980. - 13 с. 16. ANSYS CFX 10.0 Solver Models. Release 10.0: [Электронный ресурс], 2008. - 549р. - Ре- жим доступа: http://www.ansys.com.