
2. Ecoulement transitoire et les pertes d'etranglement en fonction du temps de chambres a tourbillon
La figure 2 montre la vitesse, v la perte de charge hv (hv,VD) et ζ un systeme de tuyauterie avec une diode vortex en regime transitoire (t <0 s, HE = 0, t> 0 s, HE=const. t> 0) pour le sens vers l'avant (a) et la direction d'etranglement (b). Pour la marche avant, une chambre a tourbillon produit un coefficient de perte de charge constante ? que chaque soupape fait, de telle sorte que l'ecoulement transitoire peut etre decrite precisement par l'equation de Bernoulli

Cette approche ne convient pas a la direction d'etranglement car ici ζVD, la limitation depend du temps (voir la figure 2 b, ou ζ atteint la valeur stationnaire apres 7s). C'est le principal probleme a resoudre lors du calcul d'ecoulement transitoire.
Si l'on ajoute une diode vortex a un systeme de tuyauterie, la diode est comme un accumulateur d'energie supplementaire lorsque l'energie cinetique de l'ecoulement tourbillonnaire (voir chapitre 3) determine la perte de charge de la chambre de vortex. Les experiences (conditions stationnaires) ont montre que la cinetique EVD energie dans une chambre a tourbillon diode est proportionnelle a la perte de charge dans la diode vortex. Facteur KEkin [Nm / (mWS)] decrit la relation entre l'energie cinetique EVD dans la diode et les pertes par pompage hV, VD. hv, VD peut etre calculee par.
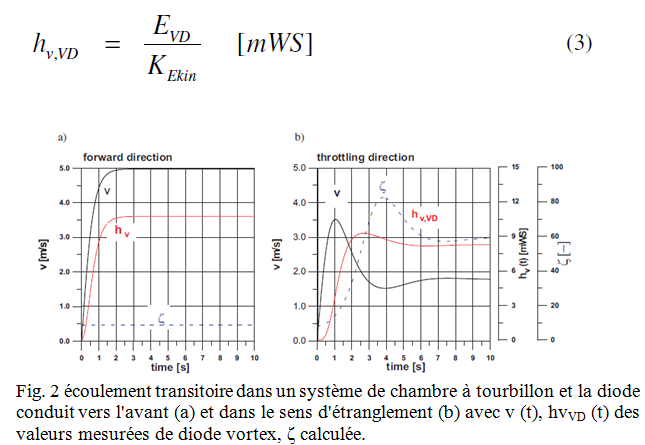
Dans ce qui suit, l'equation (3) sera egalement utilise pour decrire l'ecoulement transitoire, dans l'hypothese quasi etat d'equilibre avec
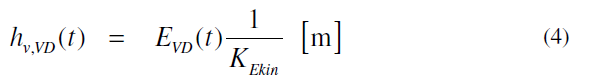
Pour l'ecoulement transitoire, cela signifie que la perte d'etranglement hv, VD (t) est egalement proportionnelle a la fois en fonction de l'energie cinetique EVD (t) dans la diode. Cela conduit a la «etendu» l'equation de Bernoulli avec

De eq. (3), EVD peut etre calcule pour des conditions stationnaires, mais la facon dont l'energie cinetique dans la chambre de vortex va changer au cours de la periode transitoire est encore inconnue. Ce sera derivee dans ce qui suit.
Conditions stationnaires dire un equilibre entre apport energetique et rendements de dissipation, et cette condition limite.
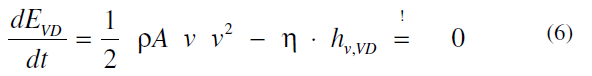
Il est evident que η doit dependre des parametres typiques geometriques et est specifique a chaque diode vortex.
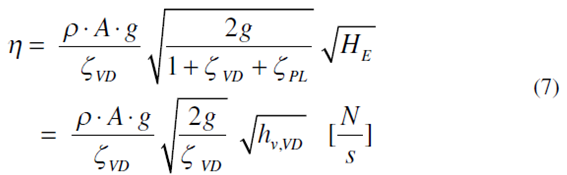
Nous avons ainsi pu calculer η pour des conditions stationnaires. Conformement a la premiere hypothese avec hv, VD (t) = EVD (t) / KEkin, η de l'equation. 7 peut etre utilise pour le calcul des ecoulements transitoires, de sorte que nous pouvons calculer l'inconnu energie cinetique EVD (t) de la definition «elargie» l'equation de Bernoulli (5). Nous remplacons hv, VD dans (6) en utilisant l'equation. (4) et d'obtenir l'equation differentielle pour EVD sous la forme
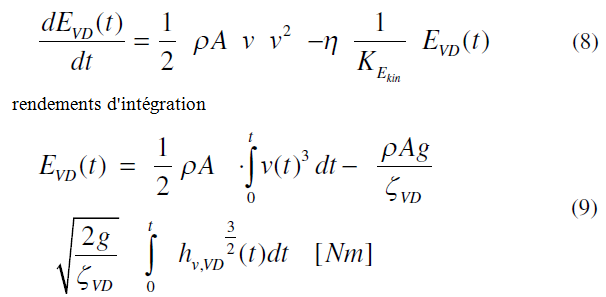
Nous avons donc le systeme des deux equations differentielles (5) («etendu» l'equation de Bernoulli) et (9) qui peut etre regle pas a pas pour les deux variables v (t) et EVD (t) pour les conditions aux limites donnees (par exemple EVD (t = 0) = 0, V (t = 0) figure 2b et la figure 6).
L'etape suivante consiste a verifier si les hypotheses correspondent a la realite. Dans de nombreuses experiences, v (t) et hv, VD (t) ont ete echantillonnes.
L'etape suivante consiste a verifier si les hypotheses correspondent a la realite. Dans de nombreuses experiences, v (t) et hv, VD (t) ont ete echantillonnes.
Avec v (t) et hv, VD (t) et ζVD (pour des conditions stationnaires), eq. 9 permet de calculer Ev (t). La figure 3 montre les correlations entre Ev (t) et hv, VD (t) (r2=0,99) pour des conditions transitoires.
Discussion des resultats et resume
La methode presentee ici permet de calculer transitoire debit dans les diodes vortex en enquetant sur les aspects cinetiques. Compare avec des methodes qui ont ete utilisees jusqu'a present et qui sont basee sur des fonctions de poids que les caracteristiques de chaque systeme, les processus decrit ici est nettement plus facile, ce qui est particulierement important dans la simulation numerique.
Il a pu etre demontre que la meme relation proportionnelle entre la perte des gaz et des etats d'energie cinetiques decrivant des ecoulements stationnaires est egalement valable pour l'ensemble du processus d'ecoulement transitoire. Par un simple equilibre de l'energie cinetique, il est possible de determiner la perte d'etranglement en fonction du temps ainsi que le coefficient de perte de ζ.
Specifique l'energie cinetique est le parametre le plus important pour la conception d'un Diode vortex. L'energie cinetique specifique est proportionnelle a etrangler perte, depend des dimensions et determine les parametres hydrauliques ainsi que la question de combien de temps il faut jusqu'a ce que l'oscillation a mis en place. Ces parametres essentiels sont tributaires d/h
Pour la simulation numerique, la solution presentee ici peut etre a la «etendu» l'equation de Bernoulli, qui est appropriee pour alterations lentes de l'etat, pour les oscillations, par exemple dans des chambres a eau ou dans des systemes avec une chambre a air et le coussin de gaz, ou en tant que Module de calcul de l'eau-de marteau programmes qui fournit le coefficient de perte de ? en fonction du temps. Pour les processus de flux de vortex dissolution, ce calcul methode donne des resultats acceptables. Neanmoins, des recherches complementaires sont necessaires. L'Institut fur Wasserbau, Lehrstuhl fur Wasserbau und Wasserwirtschaft, a l'Universite de Stuttgart est actuellement engagee dans la recherche dans ce domaine. Les exemples presentes la effectivement se reveler la methode de calcul transitoire debit dans les tuyauteries.
Ñïèñîê èñïîëüçîâàííîé ëèòåðàòóðû
JOURNAL OF HYDRAULIC RESEARCH, VOL. 41, 2003, NO. 1