Назад в библиотеку

Использование модульного принципа при моделировании движений в процессе сборки в автоматическом сборочном роторе

Авторы: О.О Кульбида., А.Л. Ищенко, Л.Н. Феник, Е.А. Понамарева
Источник:"Прогресивні технології і системи машинобудування". Международный сборник научных трудов. Выпуск 1,2 (43)

Введение

Современный уровень развития машиностроения предполагает уменьшение количества ручного труда и увеличение количества автоматизированных производст-венных процессов. На сегодняшний день процессы механической обработки автомати-зированы достаточно широко, процессы сборки в силу сложности реализации и много-номенклатурности соединений слабо охвачены этом процессом. Механизация в сборке составляет 40%, а автоматизация всего 5...6%. Поэтому остро встает задача создания автоматических сборочных систем обладающих достаточной гибкостью при переходе на другую номенклатуру собираемых изделий и обладающих высокой производитель-ностью для уменьшения себестоимости изделия. С этой задачей успешно могут справ-ляться сборочные автоматы роторного типа.

Работа технологической системы – сборочного ротора, состоящей из не-скольких технологических модулей – блоков технологического воздействия (БТВ), ос-нована на совмещении технологических и транспортных движений. Состав и геометри-ческие свойства механического движения модулей системы в процессе выполнения технологического процесса сборки описывают кинематические схемы. Создание кон-кретных вариантов технологических систем и их модулей невозможно без разработки принципиальных кинематических схем и учета геометрических параметров собирае-мых элементов. Это связано с тем, что в модели построения технологической системы [1-4] необходимо задание пространственных отношений. Пространственные отношения характеризуют взаимное положение элементов системы и положение их составных час-тей в пространстве и друг относительно друга. Эти отношения задаются математиче-скими функциями, которые определяют детерминированные связи между элементар-ными движениями в кинематических схемах технологических систем.

Цель проводимого исследования можно обозначить как разработку матема-тической модели процесса сборки в автоматическом сборочном роторе. Для реализации поставленной цели необходимо решение ряда задач: анализ кинематических схем сбор-ки с использованием модульного принципа для выделения идентичных схем для раз-личных модулей соединения; описание сложного движения деталей и БТВ в системе координат ротора для выделенных схем сборки.

Основное содержание и результаты работы

Представляет интерес сопоставить кинематику типовых соединений, рас-сматриваемых в теории взаимозаменяемости и технических измерений. Используем модульный принцип, предложенный проф. Базровым Б.М. Согласно [5] совмещение модулей поверхностей детали создает соединение, которое называется модулем соеди-нения. Плоские, шпоночные и шлицевые соединения соответствуют модулю соедине-ния МС1, резьбовые цилиндрические и конические соединения соответствуют модулям МС2 и МС3, цилиндрические гладкие соединения соответствуют модулю МС4, кони-ческие – МС6, а сферические – МС7. Модуль МС5 не охвачен типовыми соединения-ми.

Рассмотрим кинематику наиболее распространенных модулей соединений: соединение по плоским поверхностям (МС1), резьбовые цилиндрические соединения (МС2) и цилиндрические гладкие соединения (МС4).

Для проведения кинематического анализа каждое из соединений рассмотрим в системе координат БТВ, в которой базовая деталь q (деталь к которой присоединяют) и присоединяемая деталь p имеют возможность совершать трансляцию– ? и ротацию – ? вдоль соответствующих осей. Для удобства представления информации результаты анализа сведем в таблицу 1.

После анализа кинематических схем сборки, представленных в таблице 1, можно обнаружить ряд совпадений кинематических схем для различных модулей со-единений. Так обнаружены следующие идентичные схемы:

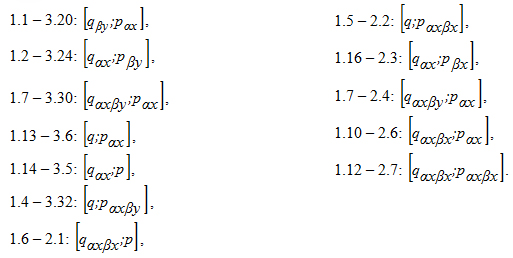
Таблица 1. Варианты кинематических схем сборки

После проведенного анализа можно сделать вывод о возможности сборки разных по типу и геометрии модулей соединения на одном оборудовании при исполь-зовании выделенных в процессе анализа идентичных схем. Это дает возможность объе-динять разнородные изделия в группы, переходить к большей серийности выпуска и использовать для сборки автоматическое оборудование, работающее по идентичным кинематическим схемам.

Проектирование технологической системы ведется на основе кинематиче-ской схемы, в соответствии с которой элементы технологической системы и их состав-ные части в процессе осуществления сборки перемещаются друг относительно друга. При исследовании процессов сборки изделий и при математическом описании про-странственных отношений элементов технологической системы возникает проблема, связанная с описанием движения собираемых изделий. Эту проблему можно решать с помощью аффинных преобразований пространства [2-4].

Для описания процесса сборки необходимо привести системы координат со-бираемых деталей, блока технологического воздействия (БТВ) и сборочного ротора к одной. Рассмотрим технологическую систему «собираемые детали – БТВ». Изменяю-щиеся во времени (при движении) координаты точек поверхностей собираемых деталей имеют вид следующего вектор - столбца:

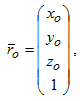
где x₀, y₀, z₀ - однородные координаты любой точки поверхности собираемой детали в системе координат детали.

В аналитическом виде переход от системы координат детали к системе коорди-нат БТВ можно описать выражением:

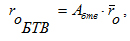
где А_БТВ - матрица перехода от системы координат i-ой детали к системе координат БТВ.

Технологическое движение сборки может состоять из одного (частный случай) или нескольких движений, обусловленных видом собираемого соединения и кинемати-ческой схемой сборки. Сложное движение, состоящее из ротации и трансляции, можно описать следующей матрицей:

где A_ox, A_oy, A_oz – матрицы перехода, описывающие ротации вдоль соответствующих осей;

A_xтр, A_yтр, A_zтр – матрицы перехода, описывающие трансляции вдоль соответствующих осей.

Составим матрицы перехода для описания движений вдоль осей для каждой де-тали в собираемом соединении. Трансляции вдоль осей будут описаны матрицами (1-3), а ротации - матрицами перехода (4-6). Трансляции вдоль осей для соответствующих деталей:

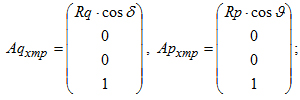
Ротации:

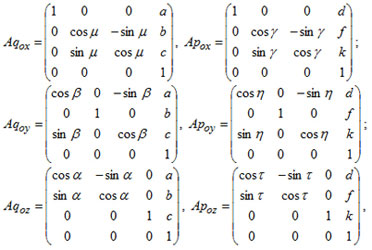
где α, β, β - углы Эйлера для базовой детали;

γ, η, τ - углы Эйлера для присоединяемой детали;

Ri – длина вектора перехода при трансляции из систем координат деталей в систему координат БТВ;

δ, ψ, ω - углы поворота, определяющие направление перехода для базовой детали;

θ, ς, ε - углы поворота, определяющие направление перехода для присоединяемой дета-ли;

a, b, c – координаты начала координат системы базовой детали в системе БТВ;

d, f, k - координаты начала координат системы присоединяемой детали в системе БТВ.

Тогда сложное движение для каждой пары выявленных выше идентичных схем будет иметь вид, представленный в таблице 2.

Таблица 2. Результаты определения матриц, описывающих сложное движение при переходе из систем координат деталей в систему координат БТВ

Следующим этапом моделирования процесса сборки при помощи аффинных преобразований координат будет переход от системы координат БТВ к системе коор-динат ротора. В процессе работы, в зависимости от компоновки ротора, БТВ может осуществлять одновременно следующие движения: ротацию вокруг оси ротора и трансляцию вдоль этой оси (см. рис. 4).

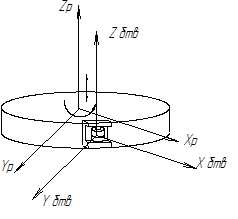
Рис.4. Схема систем коор-динат системы БТВ – ротор

Трансляция вдоль оси ОZ ротора будет описана следующей матрицей перехода

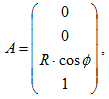
где R – длина вектора перехода при трансляции из систем координат БТВ в систему координат ротора;

φ - угол поворота, определяющий направление перехода.

Ротация вдоль оси ОZ ротора:

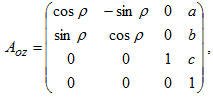
где ρ - углы Эйлера;

a, b, c – координаты начала координат системы БТВ в системе ротора.

Сложное движение, которое БТВ может осуществлять в роторе описывается матрицей:

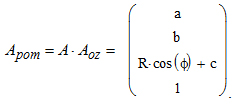
Заключение.

Таким образом, с помощью выражений (1)…(6) можно описать последовательный переход от систем координат деталей к системе координат БТВ и от системы координат БТВ к системе координат ротора, а при помощи выражения (7) описать слож-ное движение БТВ в роторе. Полученные выражения позволяют определить аналитиче-ски положения БТВ и находящихся в нем собираемых деталей в системе координат ро-тора в любой момент времени, что позволит создать системы контроля за процессом сборки и снизить количество отказов в системы.

Список использованной литературы

1. Михайлов А.Н. Основы синтеза поточно-пространственных технологических систем непрерывного действия / А.Н. Михайлов. – Донецк: ДонНТУ, 2003. – 379 с.
2. Александров П.С. Лекции по аналитической геометрии / П.С. Александров. – М.: Наука, 1968. – 912 с.
3. Перепелица Б.А. Отображение аффинного пространства в теории формообразования поверхностей резанием / Б.А. Перепелица. – Х.: Вища школа, Изд-во при Харьк. Ун-те, 1981. – 152 с.
4. Новиков М.П. Основы технологии сборки машин и механизмов / М.П. Новиков. – М.: Машиностроение, 1980. – 592 с.
5. Базров Б.М. Модульная технология в машиностроении / Б.М. Базров. – М.: Машиностроение, 2001. – 368 с.