Анализ поисковых траекторий перемещения в средствах адаптации деталей для автоматизированной сборки

Авторы: Н.С. Давыдова, А.Л. Симаков, д.т.н.
Источник: Ежемесячный научно-технический и производственный журнал «Сборка в машиностроении, приборостроении» 12-2008 (101)

Аннотация

Предложены критерии анализа поисковых траекторий в средствах адаптации деталей для автоматизированной сборки. Проведен сравнительный анализ процесса сканирования поверхности базовой детали для случаев перемещения присоединяемой детали по поисковой траектории в форме спирали Архимеда и синусоиды.

При ориентации деталей для автоматизированной сборки методом ненаправленного поиска осуществляют сканирующее перемещение присоединяемой детали по поверхности базовой детали по определенной траектории, обеспечивающей высокую степень вероятности совмещения соединяемых поверхностей. В качестве возможных вариантов траекторий автопоиска могут быть рассмотрены известные в настоящее время плоские математические кривые. Исследование влияния выбора типа траектории автопоиска на качество адаптации деталей в литературе до сих пор не проводилось.

В статье проведен анализ существующих плоских математических кривых как вариантов поисковых траекторий для реализации в средствах адаптации деталей для автоматизированной сборки.

В качестве критериев для оценки поисковых траекторий выбраны:

площадь поверхности, охватываемой при перемещении детали по кривой;
время, за которое деталь заданного размера может просканировать поверхность заданной площади;
степени свободы присоединяемой детали, необходимые для получения требуемой траектории автопоиска.

Для описания поисковых траекторий движения детали целесообразно рассмотреть существующие плоские математические кривые. Практический интерес представляют кривые, которые можно реализовать простыми механическими устройствами.

К плоским математическим кривым относят [1]:

алгебраические спирали;
периодические кривые;
алгебраические кривые.

Рассмотрим каждую из перечисленных кривых.

Существует несколько типов алгебраических спиралей [2]:

спираль Архимеда;
спираль Галилея;
спираль гиперболическая;
жезл;
спираль Корню;
спираль логарифмическая;
спираль параболическая;
розы;
спираль синусоидальная;
SICIIспираль;
спираль Ферма.

Одним из критериев выбора математической кривой в качестве траектории автопоиска в устройстве ориентации является простой способ ее получения.

Для перемещения детали по спирали Архимеда, гиперболической спирали, логарифмической спирали, SICIIспирали (рис. 1) сборочная головка должна иметь одновременно две степени свободы: поступательную вдоль некоего луча и вращательную относительно его полюса.

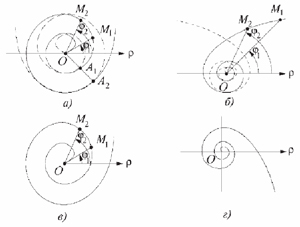
Рис. 1. Алгебраические спирали:
а – спираль Архимеда; б – спираль гиперболическая; в – спираль логарифмическая; г – SICII-спираль;
М – точка, расположенная на присоединяемой детали; r – ось полярной системы координат; О – центр полярной системы; j – угловая координата текущей точки

Спираль Галилея не позволяет выполнить сканирование поверхности базовой детали так тщательно, как спираль Архимеда. Существуют зоны необоснованного перекрытия ранее отсканированных участков.

В процессе сканирования базовой поверхности по жезлу, спирали Ферма, параболической спирали присоединяемая деталь должна иметь одновременно две степени свободы: поступательную вдоль некоего луча и вращательную, при этом необходимо предусмотреть возможность изменения направления вращения присоединяемой детали в полюсе О на противоположное.

Для поисковых траекторий в форме спирали Корню, роз, синусоидальной спирали присоединяемая деталь должна обладать двумя поступательными вдоль осей х и y и одной вращательной степенями свободы.

На основе анализа форм алгебраических спиралей можно сделать вывод, что спираль Архимеда, гиперболическая спираль, логарифмическая спираль, SICII-спираль – это наиболее простые в реализации кривые. При этом гиперболическая и SICII-спирали – раходящиеся. Спираль Архимеда и логарифмическая спираль имеют постоянный шаг, отличаются лишь направлением закручивания.

Правильный подбор параметров этих кривых обеспечит наиболее тщательное сканирование поверхности и позволит свести зоны перекрытия ранее отсканированных участков к минимуму.

Таким образом, среди алгебраических спиралей спираль Архимеда и логарифмическая спираль являются оптимальными для использования в качестве поисковых траекторий в устройствах ориентации деталей для автоматизированной сборки как кривые, наиболее просто воспроизводимые механическим устройством, обеспечивающие тщательное сканирование базовой поверхности с минимальным количеством участков, проходимых повторно в процессе ориентации.

Рассмотрим процесс сканирования поверхности базовой детали по спиральной траектории на примере спирали Архимеда как более изученной математической кривой по сравнению с логарифмической спиралью. Для анализа значений площади сканируемой поверхности при перемещении детали по спирали Архимеда и времени сканирования примем:

базовая поверхность – квадрат размером 100х100 мм;
присоединяемая деталь – цилиндр диаметром 10 мм;
скорость перемещения сборочной головки, удерживающей присоединяемую деталь, относительно поверхности базовой – 30 мм/с;
стратегия сканирования: присоединяемая деталь начинает движение из центра базовой поверхности по спирали Архимеда с шагом, равным диаметру присоединяемой детали, таким образом, чтобы последняя могла охватить поверхность максимально возможной площади, но не выходила за пределы сканируемой поверхности (рис. 2); траектория автопоиска реализуется идеально.

Спираль Архимеда – плоская трансцендентная кривая, траектория т. М (см. рис 1), движущейся из точки O с постоянной скоростью по лучу, вращающемуся около полюса O (см. рис. 2) с постоянной угловой скоростью, описываемая уравнением в полярных координатах [3]:

ρ = aφ (1)

где а – постоянная:

a = OA/2π (2)

OA – шаг спирали Архимеда [1].

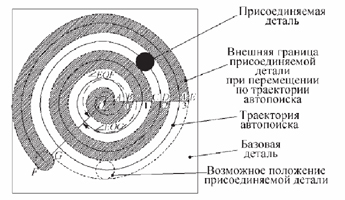
Рис. 2. Схема сканирования присоединяемой деталью поверхности базовой детали по спирали Архимеда:
1, 2, 3 – положения присоединяемой детали в конце полного круга

Площадь SА отсканированной поверхности при перемещении присоединяемой детали по поверхности базовой детали по спирали Архимеда будет равна (см. рис. 2).

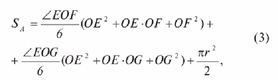
где EOF – угол, ограниченный отрезками OE и OF, рад; OE, OF, OG – длина отрезков, мм; EOG – угол, ограниченный отрезками OE и OG, рад; r –радиус присоединяемой детали, мм.

Длительность процесса сканирования поверхности базовой детали при перемещении присоединяемой детали по математической кривой равна

t=l/V

где l – длина траектории автопоиска; v – скорость перемещения сборочной головки, удерживающей присоединяемую деталь, относительно поверхности базовой детали.

Длина дуги спирали Архимеда lа между точками М1(ρ1, φ1) и М2(ρ2, φ2) (см. рис. 1) равна [2]

Кривизну K математической кривой определяют по формуле

K=1/R

где R – радиус кривизны математической кривой, в начальной точке R0 равный

R0=a/2

а в остальных точках его рассчитывают по формуле [1]

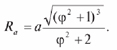
Периодические кривые представлены на рис. 3.

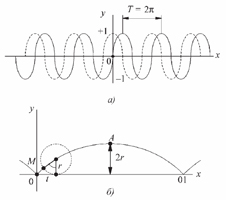
Рис. 3. Периодические кривые: а – синусоида; б – циклоида

Для сканирования поверхности базовой детали по синусоидальной поисковой траектории (см. рис. 3, а) и по поисковой траектории в форме циклоиды (см. рис. 3, б) сборочная головка должна обладать одновременно двумя поступательными степенями свободы вдоль осей x и y. При этом направление перемещения присоединяемой детали по оси y должно периодически меняться на противоположное.

Из анализа наиболее целесообразных схем сканирования поверхности базовой детали по этим траекториям автопоиска (рис. 4) видно, что для перемещения присоединяемой детали по циклоиде сборочная головка должна выполнять более сложные манипуляции, чем для получения синусоиды.

Применение синусоидальной траектории обеспечивает более тщательное сканирование базовой поверхности с минимальной площадью зон перекрытия отсканированных участков.

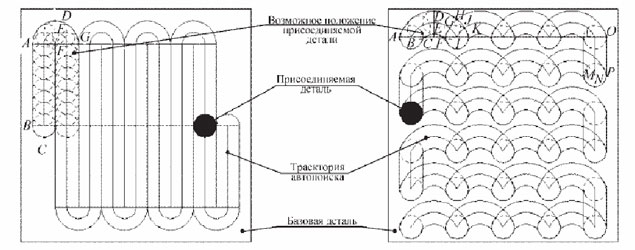
Рис. 4. Схемы сканирования присоединяемой деталью поверхности базовой детали:
а – присоединяемая деталь перемещается по траектории в форме синусоиды; б – присоединяемая деталь перемещается по траектории в форме циклоиды

Таким образом, анализ процесса сканирования поверхности базовой детали по периодической траектории выполним на примере синусоиды как наиболее простой в получении механическим устройством периодической кривой, позволяющей выполнить сканирование наиболее тщательно.

Синусоида – плоская непрерывная кривая с периодом T =2?/b, описываемая уравнением в декартовых координатах:

y = a’sin(bx+c)

где a, b, c – постоянные, определяющие степень соответственно вытянутости кривой вдоль оси ординат, сжатия кривой по оси абсцисс, величину сдвига кривой по фазе по оси абсцисс.

Параметры базовой и присоединяемой деталей, скорость перемещения сборочной головки, удерживающей присоединяемую деталь относительно поверхности базовой, те же, что и при анализе спирали Архимеда.

Исходя из принятых условий ориентации сопрягаемых деталей, оптимальную кривую автопоиска описывают следующим уравнением в декартовой системе координат:

y = 40sinx

Такая кривая позволяет наиболее тщательно выполнить сканирование за одно прохождение сборочной головки вдоль базовой детали за короткий промежуток времени. При этом присоединяемая деталь наполовину диаметра не доходит до внешней границы базовой детали, что предотвращает выход первой за пределы второй в процессе движения.

Идеально реализовать синусоиду механическим устройством невозможно, поэтому выберем схему сканирования, изображенную на рис. 4. Считаем, что стороны срезов базовой детали перпендикулярны. На участках AB присоединяемая деталь двигается строго параллельно правому срезу базовой детали из его середины. Переместившись на 35 мм, она описывает дугу окружности относительно т.F радиусом EF = 5 мм. Далее деталь снова двигается 35 мм строго параллельно правому срезу базовой детали. Аналогично реализуют отрицательную полуволну траектории.

Таким образом, формируют оптимальную для данного случая траекторию амплитудой 40 мм и периодом, равным трем диаметрам присоединяемой детали (30 мм). Присоединяемая деталь при перемещении не выходит за пределы сканируемой поверхности. Траектория автопоиска реализуется идеально.

Площадь Sс отсканированной поверхности при перемещении присоединяемой детали по поверхности базовой детали по синусоиде определим по формуле (см. рис. 4)

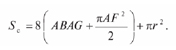
Длина дуги lc синусоиды в диапазоне полупериода равна

lc = 16AB + 8nr

При анализе изменения радиуса кривизны синусоиды примем, что его величина на линейных участках AB равна бесконечности. Кривизну синусоиды определяют по формуле (6). В вершине E радиус кривизны кривой полностью совпадает с радиусом кривизны синусоиды, описываемой уравнением в декартовой системе координат y = 40sinx, и находится по формуле

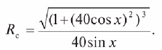
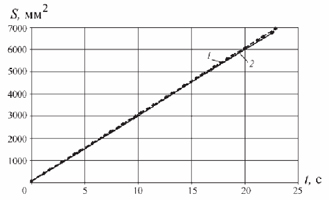
Рис. 5. Графики изменения площади сканируемой поверхности от времени:
1 – при перемещении присоединяемой детали по синусоиде; 2 – при перемещении присоединяемой детали по спирали Архимеда

Графики зависимости изменения площади сканируемой поверхности при перемещении присоединяемой детали по спирали Архимеда и синусоиде от времени изображены на рис. 5.

К алгебраическим кривым относят кубическую параболу, квадратичную параболу, улитку Паскаля, полукубическую параболу, эпициклоиду и др.

Большинство алгебраических кривых очень сложны для реализации механическими устройствами. К тому же при движении детали даже по оптимальной плоской алгебраической кривой невозможно просканировать поверхность базовой детали за один проход. Для устранения этого недостатка можно изменить схему сканирования поверхности базовой детали за счет либо смещения детали после первого прохода по траектории, либо периодического изменения параметров кривой. Это приводит к существенному увеличению времени ориентирования сопрягаемых деталей.

Таким образом, применение плоских алгебраических кривых в качестве поисковых траекторий не позволяет добиться непрерывного сканирования поверхности базовой детали присоединяемой деталью за кратчайший промежуток времени.

Анализ полученных результатов показывает, что наиболее простыми из известных математических кривых при формировании механическим устройством являются спираль Архимеда и синусоида. За один и тот же промежуток времени при одинаковых условиях, перемещая присоединяемую деталь по синусоидальной поисковой траектории, возможно сканировать большую площадь (приблизительно на 100 мм2) базовой поверхности, чем при перемещении детали по спирали Архимеда.

Кривизна спирали Архимеда достигает максимума в полюсе и равномерно уменьшается от полюса к последней точке траектории. Кривизна синусоиды максимальна в вершинах и неравномерно, скачками уменьшается по мере приближения к точкам перегиба до нуля. Кривизна синусоидальной траектории автопоиска в вершине приблизительно в 31 раз больше, чем кривизна спирали Архимеда в полюсе. Это значит, что в вершине синусоидальной траектории присоединяемая деталь двигается с высоким ускорением. Механизм перемещения сборочной головки на этом участке будет испытывать значительные нагрузки и быстрее изнашиваться.

Выводы

Наиболее предпочтительным вариантом траектории автопоиска в устройствах адаптации деталей является спираль Архимеда.

Список использованной литературы

Выгодский М.Я. Справочник по высшей математике. М.: Государственное изддво физикооматематической литературы, 2001.
Математическая энциклопедия. Ред. коллегия: И.М. Виноградов (глав. ред.) и др. Т. 1. М., "Советская энциклопедия", 1977. 1152 с.
Математический энциклопедический словарь / под ред. Ю.В. Прохорова. М.: Советская энциклопедия, 1988. 847 с