Назад в библиотеку

Модель динамики ротационной сборки цилиндрических деталей

Авторы: М.Г. Кристаль, И.А. Чувилин
Источник: Ежемесячный научно-технический и производственный журнал «Сборка в машиностроении, приборостроении» 08-2008 (97)

При автоматической сборке сопрягаемые цилиндрические детали на сборочной позиции располагаются под некоторым углом друг к другу. Это вызвано либо погрешностью их взаимного расположения, либо, при использовании эффекта наклона осей сопрягаемых деталей, служит для компенсации этой погрешности. Придерживаясь принципа свободного взаимодействия деталей на сборочной позиции, следует создать некоторые дополнительные условия, обеспечивающие совмещение сопрягаемых поверхностей.

Поскольку охватываемая деталь (валик) расположена наклонно в поле сил тяжести, то ее потенциальная энергия не является максимальной. Для ее подъема и поворота вокруг некоторой оси требуется дополнительная энергия.

Предположим, что валик является абсолютно твердым телом и расположен под углом к отверстию охватывающей детали, при этом торцы деталей контактируют между собой по трем точкам.

Заменим трехточечный контакт одноточечным в т.O пересечения осей сопрягаемых поверхностей, и примем допущение, что сила тяжести детали и ее момент относительно т.O компенсируются реакцией и некоторым моментом Mтр сил трения в этой точке.

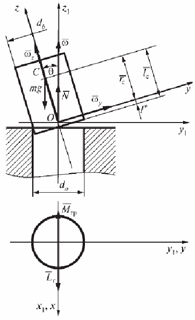
Рис. 1. Относительное расположение сопрягаемых деталей в подвижной и неподвижной системах координат:
N – обобщенная реакция псевдоопоры в т. О; q – угол нутации валика; w – вектор угловой скорости валика;
wy, wz– проекции w на оси координат; Lг – гироскопический момент; lс – расстояние от центра масс валика до его торца

Введем неподвижную Ox1y1z1 и подвижную Oxyz системы координат с центрами в т. O таким образом, чтобы ось Oz1 совпадала с осью охватывающей поверхности (втулки), а ось Oz – с осью наклонного валика (рис. 1). Таким образом, к твердому телу, имеющему одну неподвижную точку, будет приложена только одна активная сила — сила тяжести.

Центр тяжести тела обозначим C (см. рис. 1) с координатами xC, yC, zC в подвижной системе координат. Тогда радиус-вектор т. C равен

где i, j, k– единичные векторы подвижных осей координат.

Представим силу P разложенной в проекциях по неподвижным осям координат: Px1=0; Py1=0; Рz1=-mg. Здесь ось Oz1 направлена вертикально вверх. Тогда

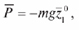
где z1 – единичный вектор на неподвижной оси Oz1, а знак минус отражает направление силы P тяжести (вертикально вниз). Тогда проекции силы P на подвижные оси системы координат Oxyz с учетом значений направляющих косинусов, используемых в кинематических уравнениях Эйлера, будут иметь вид

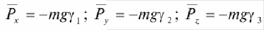
где у1, у2, у3 – направляющие косинусы в кинематических уравнениях Эйлера:

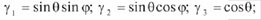
где ? – угол собственного вращения валика.

Момент Mо(P)силы P относительно неподвижной т. O равен

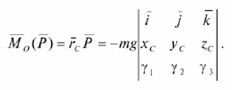
Подведение дополнительной энергии к данной механической системе можно осуществить за счет придания валику вращательного движения с угловой скоростью w, вектор которой направлен вдоль оси Oz1.

Тогда динамические уравнения Эйлера движения тела вокруг неподвижной точки в проекциях на подвижные оси под действием только силы собственной тяжести имеют вид [1]

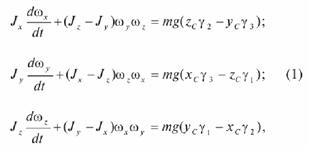
где Jx, Jy, Jz и wx, wy, wz – моменты инерции валика относительно осей подвижной системы координат и проекции угловой скорости w на эти оси соответственно.

Для решения динамических уравнений Эйлера (1), содержащих шесть неизвестных функций времени wx, wy, wz, у1, у2, у3, используем уравнения Пуассона:

где t – время.

В рассматриваемом случае сила тяжести валика уравновешивается реакцией опоры и моментом Mтр сил трения в неподвижной опорной т.О и в каждый конкретный момент времени никакие другие силы не действуют на тело, что удовлетворяет случаю Лагранжа [3], когда

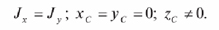
Тогда в соответствии с [3] возникающий гироскопический момент Lг, действующий перпендикулярно плоскости (рис. 1), в которой лежат векторы w и wz, будет равен

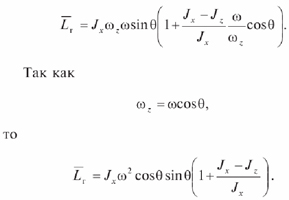
Согласно [3] движение гироскопа является устойчивым при собственном вращении его вокруг большой или малой осей эллипсоида инерции, а вращение вокруг средней оси этого эллипсоида неустойчиво.

Поэтому, если начальный угол Oo нутации (он же начальный угол относительного расположения осей сопрягаемых поверхностей) будет меньше угла Oкр между средней и большой осью эллипсоида инерции, то при достижении некоторого значения угловой скорости w = wкр охватываемая деталь начнет поворот (в соответствии с правилом Жуковского) до совмещения осей сопрягаемых деталей.

Рис. 2. Зависимости величины предельных начальных углов Окр(e) и Окр(v) наклона осей сопрягаемых поверхностей

Jx – экваториальный момент инерции валика относительно приведенной точки вращения; Jz – главный момент инерции валика относительно оси собственного вращения.

С другой стороны, угол Окр ограничен условием относительного расположения сопрягаемых поверхностей под углом между осями. Его величину определяют:

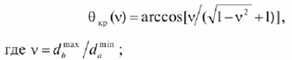
dbmax – наибольший диаметр охватываемой поверхности; damin – наименьший диаметр охватывающей поверхности.

Движение, описанное выше, начинается после того, как величина гироскопического момента превысит величину момента сил трения:

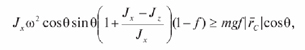
где f – коэффициент трения скольжения материала сопрягаемых деталей.

Из этого выражения определяют величину критической угловой скорости

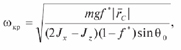
где Оо меньше Окр – допустимый угол наклона осей сопрягаемых деталей, который выбирают меньшим из О’кр и Окр;
f’ – приведенный коэффициент трения;
  - поправочная функция, определяемая из сравнения теоретических и экспериментальных результатов и компенсирующая принятые допущения (a = 0,3192; b = 0,03574 рад);
a и b – коэффициенты поправочной функции.

До момента времени t1 достижения системой скорости wкр, относительного движения деталей не происходит, так как гироскопический момент Lг уравновешивается моментом сил трения, и уравнение движения на этом этапе имеет вид

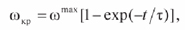
где τ – постоянная времени разгона. Она определяется инерционными свойствами рабочего ротора установки и характеристиками турбинного привода, и в каждом конкретном случае определяется индивидуально, а проще всего – экспериментально, путем математической обработки кривой разгона ротора; wmax – максимальная скорость вращения ротора сборочного устройства.

Отсюда величину τ можно вычислить как

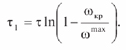
Тогда на втором этапе дифференциальное уравнение поворотного движения в условиях трехточечного контакта торцов сопрягаемых деталей при t = [t1, t2], будет иметь вид

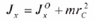  - момент инерции охватываемой детали относительно оси Ox;
Jxо – центральный момент инерции относительно той же оси;
d – коэффициент демпфирования системы, определяемый из эксперимента;
f – коэффициент трения скольжения;

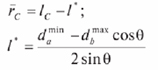
При достижении двухточечного контакта полученные выражения сохраняют свой вид. Вычисление заканчивается к моменту времени t2, при достижении углом О значений, близких к

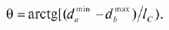
Полученная модель позволяет определить время tс протекания процесса ротационной сборки цилиндрических деталей как сумму:

tc = t1 + t2

Проверка адекватности предложенных расчетов выполнена на экспериментальной установке (рис. 3) для ротационной сборки цилиндрических роликовых подшипников [2] при помощи скорост ной видеосъемки камерой VSSFAST. На рис. 4 представлена зависимость величины критической скорости wкр от величины начального угла Оо пересечения осей сопрягаемых поверхностей, а на рис. 5 – теоретические и экспериментальные законы О(t) изменения угла О в процессе ротационной сборки.

Рис. 3.Экспериментальная установка для ротационной сборки

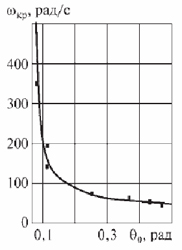
>Рис. 4. Влияние начального угла Оо пересечения осей сопрягаемых деталей на величину критической угловой скорости wкр вращения ротора

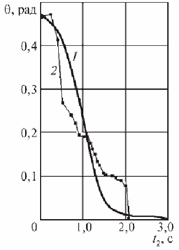
Рис. 5. Законы О(t) изменения угла между осями сопрягаемых поверхностей:
1 – теоретический; 2 – экспериментальный

Выводы.

Экспериментально было установлено:

с увеличением начального угла наклона осей сопрягаемых поверхностей время поворота охватываемой детали до совмещения осей сопрягаемых поверхностей уменьшается, но одновременно увеличивается время разгона до критической скорости, при которой начинается процесс совмещения осей, однако суммарное время сборки практически остается неизменным;

при начальных углах наклона валика, меньших Окр, обеспечивалось гарантированное сопряжение деталей.

Таким образом, теоретически определены и экспериментально обоснованы условия и время выполнения ротационной автоматической сборки цилиндрических соединений с зазором.

Список использованной литературы

1. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики: В 22х т., Т. II. Динамика. Изд. 66е перераб. и доп. М.: Наука, Главная редакция физикооматематической литературы, 1983. 640 с.
2. Патент РФ № 2239735, МКИ 7 F 16 С 43/06. Устройство для сборки радиальных роликовых подшипников / М.Г. Кристаль, Е.В. Стегачев, А.В. Широкий. Опубл. БИ № 31, 10.11.2004.
3. Добронравов В.В. и др. Курс теоретической механики. Изд. 33е, перераб. Учебник для вузов. М.: Высш. школа, 1974. - 528 с.