Abstract
Introduction
- Introduction
- 1. L'actualité du sujet
- 2. Le but et les objectifs de la recherche, les resultats attendus
- 3. Les modèles mathématiques de manipulateur pneumatique avec une cinématique de série.
- Conclusion
- Liste des sources
Introduction
On considère les avantages et les inconvénients d'un manipulateur pneumatique avec une cinématique de série pour le triage de produits du gabarit petit. On examène des méthodes de calcul et des modèles mathématiques de manipulateur pneumatique avec une cinématique de série.
Dans les entreprises ukrainiennes qui nécessitent au triage de produits en paquets petits, ce travail se fait manuellement à cause du manque des fonds de roulement pour l'automatisation. Pour ce type de production est conseillé d'utiliser des manipulateurs simplifiée, qui ont le coût faible et le retour rapide des investissement, Ce sont des manipulateurs de série de la commande pneumatique et électropneumatique. La simplicité relative de la configuration des commandes pneumatiques et de leur entretien, qui sont entraînés par l’alimentation d’une ligne des machines pneumatiques et des actionneurs (air vicié est évacué directement dans l'atmosphère sans l’aide des lignes de décharge), facilite le processus de la mise en application en production des lignes automatisées.
1. L'actualité du sujet
Le processus du triage des produits en paquet compact dans les productions modernes ukrainiennes est à la stade initiale de l'automatisation. La tâche du triage des produits dans la plupart des enterprises ukrainiens on résoudre en utilisant le travail manuel. La solution rationnelle est l'introduction de robots industriels - l'un des moyens les plus perspectifs de l'automatisation complexe. L'utilisation de robots permet d’augmenter considérablement la productivité, sauver l'homme de la monotonie du travail lourd et dangereux, et de réduire les coûts de production.
En plus de choisir le type de construction de robot industriel une tâche importante pour le constructeur est de sélectionner le commande d’amenet, en garantant un mouvement positionné sur les chaînons du manipulateur. On distingue selon le type d'énergie utilisée les commandes d’amenet suivantes: lpneumatiques, hydrauliques, électriques et combinées. Le choix du type de la commande est une partie de la problématique générale du développement et de la construction du manipulateur. Ce choix dépend des facteurs nombreux: du type de la charge, des déplacements nécessaires linéaires et angulaires, de la vitesse et des lois du mouvement de l'organe du travail, du nombre de points et de la précision du positionnement, des conditions d'exploitation de la commande et de l'environnement.
Pour le choix correct de la commande on a besoin d’analyser ses avantages et ses inconvénients pour leur utilization en type particulier de production. Ainsi que il faut avoir la compréhension de la nature des processus, qui se déroulent en commande, pour la construction des modèles mathématiques adéquats.
2. Le but et les objectifs de la recherche, les resultats attendus
Considérer les avantages et les inconvénients d'application des commandes pneumatiques aux manipulateur avec une cinématique de série pour le triage des produits des gabarits petits, leur structure, les principes du calcul des paramètres et des modèles mathématiques des commandes pneumatiques utilisés dans des manipulateurs de la cinématique de série, et à la base desquelles développer la structure du manipulateur industriel pour les conditions concrètes.
L’autre direction future de recherche sera la détermineation les paramètres cinématiques et dynamiques du manipulateur pneumatique pour une entreprise donnée et la modélisation des pneumatiques en programme FluidSIM avec le but d'affiner les paramètres de construction des éléments du manipulateur.
3. Les modèles mathématiques de manipulateur pneumatique avec une cinématique de série.
Les mécanismes pneumatiques exécutifs sont des installations qui transforment l'énergie du gaz serré à l'énergie mécanique du mécanisme de sortie ou le groupe de sortie de la commande développant l'effort jusqu'à 200 N. L’utilisation des mécanismes à piston, appelé comme les pneumocylindres, dans les commandes pneumatiques est conditionné par la simplicité constructive, par la sécurité et la garantie des efforts considérables ouvriers.
Les commandes pneumatiques, qui appliquent dans les manipulateurs en série pour le triage des produits des dimensions petites, possèdent une série des avantages et les manques.
Les caractéristiques positives sont:
- La simplicité et la sécurité des structures;
- La grande vitesse du groupe de sortie de la commande (au déplacement linéaire jusqu'à 1 m/s, à la rotation jusqu'à 60 tr/s);
- Comme le corps ouvrier l'utilisation de l'air comprimé étant la source écologiquement propre;
- Une haute exactitude du positionnement selon les points définis par les appuis rigides mécaniques;
- La possibilité du travail aux milieux agressifs et les explosibles.
Les caractéristiques negatives de la commande pneumatique sont:
- La capacité basse de sortie;
- L'exactitude du positionnement peu élevée sans les appuis mécaniques;
- Une grande quantité des éléments non linéaires dans le système de gestion, ainsi que dans le moteur pneumatique.
Il y a trios types de calcul des commandes pneumatiques:
- Le calcul des commandes pneumatiques, à qui le dynamisme des lignes de transmission et les procès d'onde dans les cavités des commandes pneumatiques n'influencent pas pratiquement à leur travail.
- Le calcul des commandes pneumatiques des volumes petits. Dans tels commandes pneumatiques le volume des cavités ouvrières est comparable ou est plus petit, que les volumes des conduites connectées à eux. Finalement la ligne exerce l'influence essentielle sur le dynamisme de la commande pneumatique. C'est pourquoi à la rédaction des modèles il faut prendre en considération les procès dans les lignes de transmission.
- Les commandes pneumatiques complexes (suivants et de position).
Quand on calcule des dimensions des commandes typiques les caractéristiques typiques d'entrée et de sortie des tuyaux sont pris en compte comme des résistances supplémentaires, et la quantité de tuyaux dans le calcul est ajouté aux volumes appropriés des cavités de la commende.
Pneumatique à manipulateurs est fait usage de plus hautes Les actionneurs linéaires et tournantes ont l’usage le plus haute dans les manipulateurs avec la commande pneumatique. On compose les modèle mathématique de ces mécanismes.
Modèle mathématique de la commande pneumatique linéaire. [7]
Schéma de calcul de la commande pneumatique linéaire est présentée sur la fig. 1.
Modèle mathématique de la commande pneumatique est le système des équations différentielles décrivant le mouvement du corps de direction et la variation de la pression dans les cavités de l'actionneur. Ainsi, le modèle mathématique de la commende pneumatique comprend les équations suivantes:
- l'équation du mouvement de l'organe exécutif;
- l'équation de la variation de pression dans la chambre du refoulement;
- l'équation de la variation de pression dans la chamber de l’échappement.
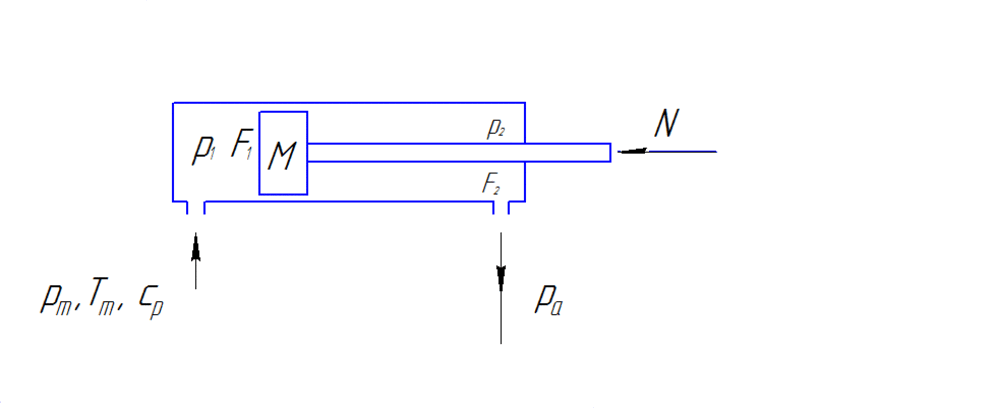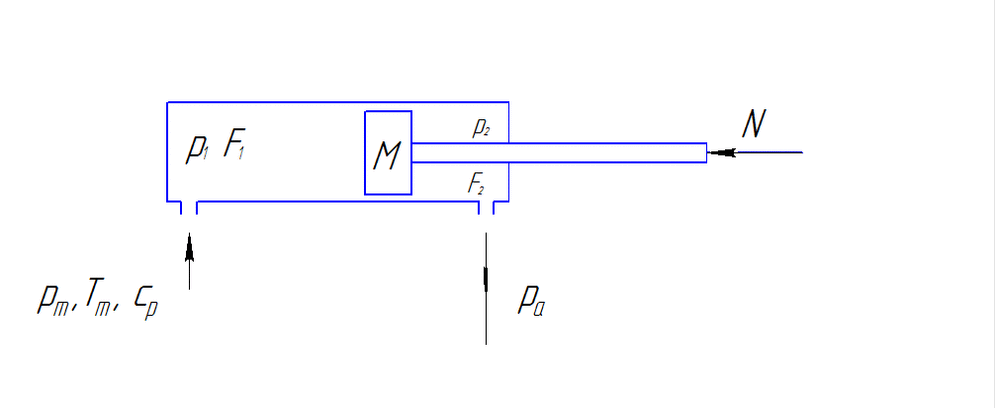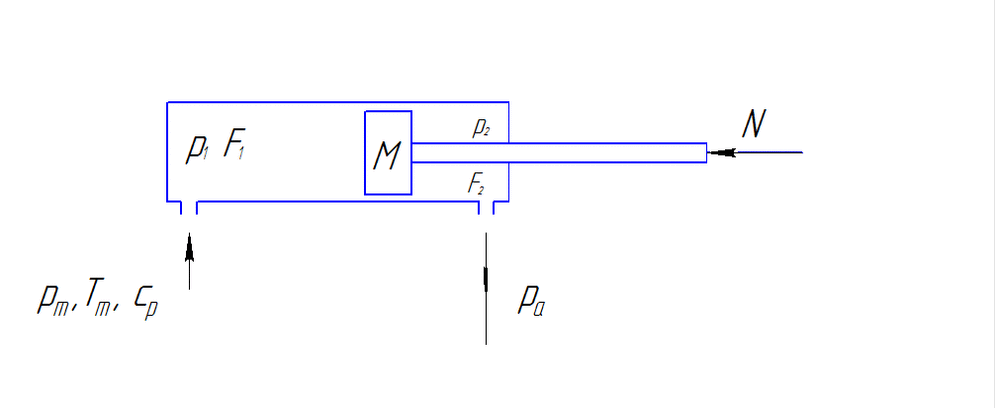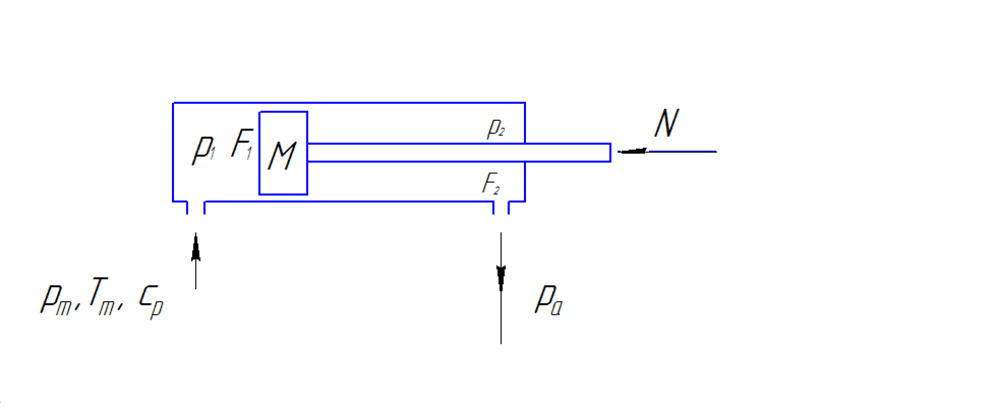
Fig. 1 – Schéma de calcul de la commande pneumatique linéaire (Animation est faite avec l'aide de GIF Animator. Consiste en 5 images avec l'intervalle en 600 ms.)
Modèle mathématique de la commande pneumatique linéaire typique peut être représentée comme:
L'équation du mouvement de la commande:
M(d²x/dt²)=p1F1-p2F1-pA(F1-F2)-N.
L'équation décrivant le changement de la pression Р1 dans la cavité de refoulement:
dp1/dt=((kƒ1√(RTM))/(F1(x+x01)√(ζ1)))√(p²M-p²1)-(kp1dx/(x+x01)dt).
L'équation de le changement de la pression du gaz dans la cavité de sortie:
(dp2/dt)=-((kƒ2√(RTM))/(F2(S-x-x02)√(ζ2)))(p2/p1)(k-1)/2k√(p²2-p²A)+(kp2dx/(S-x-x02)dt).
Pour le cas lorsque le cylindre à l’air se trouve dans la position gauche extrême, il faut ajouter une condition pour les équations resultants du modèle mathématique:
(d²x/dt²)=(dx/dt)=x=0, si x≤0.
Il faut écrire la condition, qui limite la coordonnée x de l'actionneur de longueur de course S, pour le cas où le piston attaint à la fin la position gauche extrême:
(d²x/dt²)=(dx/dt)=0 et x=S, si x≥S.
Modèle mathématique de la commande pneumatique tournante. [7]
Schéma du calcul de la commande pneumatique tournante est montré dans la fig. 2.
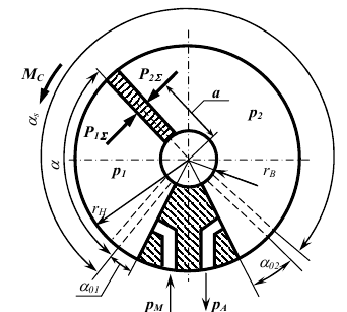
Fig. 2 – Schéma du calcul de la commande pneumatique tournant
Modèle mathématique de la commande pneumatique tournante typique peut être représentée comme:
L’équation du movement de la commande:
J(d²α/dt²)=KV(p1-p2)-Mc.
L’équation du changement de la pression dans la cavité du refoulement de la commande:
(dp1/dt)=((kƒ1√(RTM))/(KV(α+α01)√(ζ1)))√(p²M-p²1)-(kp1dα/(α+α01)dt).
L'équation du changement de la pression dans la cavité d'échappement de la commende:
(dp2/dt)=((kƒ2√(RTM))/(KV(αS-α+α02)√(ζ2)))(p2/pM)(k-1)/2k√(p²2-p²A)+(kp2dα/(αS-α+α02)dt).
Dans l'équation du mouvement on impose des restrictions sur le coin:
(d²α/dt²)=(dα/dt)=α=0, si α≤0,
(d²α/dt²)=(dα/dt)=0 et α=αS, si α≥αS.
où α — coordonnée angulaire de la position du piston.
Les conclusions et les orientations pour la recherche future. Production avec le triage des produits des gabarits petits ont besoin d'automatisation qui peut être atteint grâce à l'introduction de robots manipulateurs. Pour ce type de production est suffisant d'utiliser un manipulateur à deux chaînons de série avec les commandes pneumatiques linéaires et rotatifs.
L’autre direction future de recherche sera la détermineation les paramètres cinématiques et dynamiques du manipulateur pneumatique pour une entreprise donnée et la modélisation des pneumatiques en programme FluidSIM avec le but d'affiner les paramètres de construction des éléments du manipulateur.
Conclusion
Production avec le triage des produits des gabarits petits ont besoin d'automatisation qui peut être atteint grâce à l'introduction de robots manipulateurs. Pour ce type de production est suffisant d'utiliser un manipulateur à deux chaînons de série avec les commandes pneumatiques linéaires et rotatifs.
L’autre direction future de recherche sera la détermineation les paramètres cinématiques et dynamiques du manipulateur pneumatique pour une entreprise donnée et la modélisation des pneumatiques en programme FluidSIM avec le but d'affiner les paramètres de construction des éléments du manipulateur.
Liste des sources
- Шаньгин Е.С. Управление роботами и робототехническими системами. Конспект лекций. – Уфа, 2005.
- Донской А. С. Математическое моделирование процессов в пневматических приводах: Учеб. Пособие. – СПб.: Изд-во Политехн. ун-та, 2009. – 121 с.
- Пашков Е., Осинский Ю., Четверкин А. Электропневмоавтоматика в производственных процессах. 2003. – 495 с.
- Пашков Е., Осинский Ю. Промышленные мехатронные системы на основе пневмопривода. 2008. – 388 с.
- Пашков Е., Васютенко А.П., Осинский Ю., Поливцев В.В., Волошина Е.А. Автоматизация в промышленности: лабораторный практикум. Часть ІІ. Транспортно-накопительные, загрузочные, сборные и контрольно-измерительные устройства, 2009. – 224 с.
- Губарев А.П., Левченко О.В. Механотроника: от структуры системы к алгоритму управления. Киев, 2007. – 180с.
- Белоусов А. П. проектирование станочных приспособлений: Учебное пособие для учащихся техникумов. – 3-е изд., перераб. и доп. – М.: Высш. школа, 1980. – 240 с., ил.
- Hesse S. 99 Examples of Pneumatic Applications . – Festo AG & Co, 2001. – 120 p.
- Хессе С. Рационализация подачи небольших заготовок. 2004. – 112 с.
- Хессе С. Сжатый воздух как носитель энергии. Подготовка и распределение. 2004. – 128 с.
- Хессе С. Пневмомускул за работой. 150 примеров применения пневматического мускула. 2004. – 140 с.
- Lung-Wen Tsai Robot analysis: the mechanics of serial and parallel manipulators. – New York: Wiley, 1999. – 505 p.
- Преде Г., Шольц Д. Электропневмоавтоматика, 2004, 292 с.
- Близенер Р., Эбель Ф., Лёфер К. и др. Свободно-программируемые контроллеры. 2005. – 196 с.
- [Электронный ресурс]. – Режим доступа: http://www.rekord-eng.com /.... Режим доступа 7.05.2013
- Федорец В.А. и др. Гидроприводы и гидропневмоавтоматика станков. К., 1987, — 375 с.
- Сырицын Т.А. Эксплуатация и надежность гидро- и пневмоприводов. М., 1990. – 249 с.
- Попов Д.Н. Динамика и регулирование гидро- и пневмосистем. М., 1976. – 424 с.
- Наземцев А.С. Гидравлические и пневматические системы. Часть 1. Пневматические приводы и средства автоматизации : Учебное пособие М., ФОРУМ, 2004. - 240 с.
- Аш. Ж. Датчики измерительных систем: В 2-х книгах. Книга 1. М., 1992. – 480 с.
