Залежність опору руху коченню та ковзанню від співвідношення модулів пружності при стисненні
Автори: Смирнов Г.Ф., Бондаренко Л.М.
Джерело: Журнал «Теорія і практика металургії». – 2002. – №5-6. – С. 72-75.
Анотація
УДК 621.746.047
Смирнов Г.Ф., Бондаренко Л.М. Залежність опору руху коченню та ковзанню від співвідношення модулів пружності при стисненні. Визначені опори коченню циліндра (ролика) та кулі (шарика) по направляючих із матеріалів, які мають суттєво різні модулі пружності при удавлюванні; розглянута можливість заміни підшипникового вузла кочення вузлом ковзання, або навпаки, виходячи із умови однакової величини опору коченню.
1. У машинобудівній практиці досить часто зустрічаються випадки, коли модулі пружності матеріалів тіл кочення і направляючої мають суттєво різні за величиною модулі пружності при вдавлюванні (стрічка конвеєра – ролик, шків – пас, обгумоване колесо – стальна направляюча і т. ін.).
Звичайно, необхідно знати, як впливає відношення модулів пружності тіла кочення Е1 та направляючої Е2 на абсолютну W та відносну W/[Р] величини опору руху і перевагу яким відношенням Е2/Е1 треба давати.
Інколи виникає необхідність вирішення питання еквівалентної заміни вузлів тертя кочення на ковзання або навпаки з точки зору збереження величини опору руху. Ця ситуація актуальна для металургійного устаткування, що працює в умовах агресивного середовища.
Розглянемо спочатку схему дотику циліндр-площина, змінюючи, наприклад, модуль пружності колеса Е1 при постійній його величині для рейки Е2.
В роботах [1-3] доведено, що коефіцієнт тертя кочення k може бути переданий через півширину статичної плями контакту b. Якщо вважати коефіцієнт Пуассона μ для матеріалу колеса і рейки таким, що μ2 << 1, то півширина плями контакту:
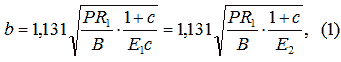
де с – будь-яке додатне число, с = Е2/Е1;
В – ширина рейки;
Р – допустиме навантаження;
R1 – радіус колеса.
Величину Р знайдемо із найбільш допустимих напружень:
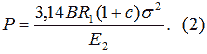
Підставивши значення Р із формули (2) у вираз для b, отримаємо:

Величина коефіцієнта тертя кочення при початковому лінійному контакті згідно досліджень, наведених у роботах [2] і [3],
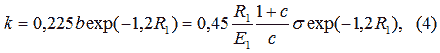
а опір коченню:
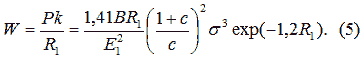
Залежність опору руху колеса радіусом R1 =50 мм від с = Е2/Е1 при Е2 = 20.105 МПа; σ = 800 МПа; В = 20 мм показана на рис. 1, а.

Рисунок 1. Залежність від відношення модулів пружності тіла кочення та площини:
а – лінійний; б – точковий; 1 – опору руху; 2 – відносного опору W/Р; 3 – коефіцієнта тертя кочення; 4 – максимальної доступної сили
Розглянемо аналогічну задачу і для схеми дотику сферичне тіло-площина. Формули, відповідні формулам (1)-(5), мають вигляд:

Значення для R1 і Е2 візьмемо, як і в попередньому прикладі, а величину допустимих контактних напружень приймемо на 40 % більшою, оскільки початковий контакт точковий, тобто σ = 1120 МПа.
Залежності для точкового контакту показані на рис. 1, б.
2. Інколи перед конструктором виникає питання: якому вузлу тертя віддати перевагу – кочення чи ковзання.
Розглянемо таку задачу: абсолютно жорстка пластина розміром В×l завантажена силою Р і під дією сили:
де f – коефіцієнт тертя ковзання.
Будемо вважати, що напруження між пластинами σ не перевищують допустимих, тобто контакт пружний.
Тепер уявимо, що пластина замінена циліндром тієї ж довжини В і завантажена тією ж силою Р.
Опір коченню циліндра:
де R – невідомий радіус циліндра.
Опори пересуванню циліндра і пластини будуть рівними у випадку, коли:
або коли коефіцієнт тертя кочення k циліндра по площині буде дорівнювати:
Дещо змінивши запис формул пункту 1, запишемо вираз для величини k у випадку схеми дотику циліндр-площина:
Порівнявши праві частини формул (7) і (8), отримаємо, що:
Природньо, що в останній формулі величина Р повинна бути такою, щоб напруження не перевищували прийнятих для пластини,тобто:
Знайшовши звідси максимальне значення сили Р і підставивши у рівняння (9), отримаємо, що із умови рівності напружень і опорів пересуванню коченню радіус циліндра повинен скласти:
У разі, наприклад, В×L = 50×100 мм; [σ] =850 МПа; E = 2,1·105 МПа характер зміни радіуса R від коефіцієнта тертя ковзання показано на рис. 2. Відзначимо, що якщо гадана величина радіуса R менше 40 мм, то можна скористатися, замість (11), формулою:
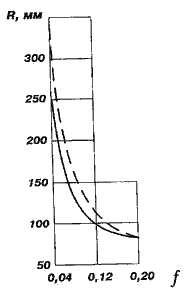
Рисунок 2. Залежність від коефіцієнта тертя ковзання радіуса циліндра, при якому контактний тиск і опір коченню відповідають їх значенням при терті ковзання (– – без врахування експоненти)
Проведемо аналогічні викладки, замінивши тертя ковзання двох площин коченням кулі; не будемо забувати, що контактні напруження при початковому контакті необхідно брати приблизно на 40 % більшими, ніж при лінійному.
Для схеми дотику сферичне тіло-площина коефіцієнт тертя кочення при тих же умовах, що і вище:
Порівнявши праві частини формул (7) і (12), отримаємо:
Якщо підставити сюди величину Р із формулі найбільших контактних тисків, отримаємо:
Відзначимо [4], що величини ехр(–1,2k) і ехр(0,2R) в формулах (12) і (14) визначають коефіцієнт гістерезисних витрат при коченні, тобто ал = ехр(–1,2R) і аT = ехр(0,2R).
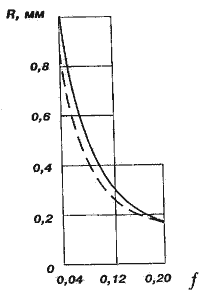
Рисунок 3. Залежність від коефіцієнта тертя ковзання радіуса сфери, при якому контактні тиски і опір руху відповідають їх значенням при терті ковзання двох площин (– – без врахування експоненти)
Аналіз наведених формул і графіків на рис. 1,2 і 3 дозволяє зробити такі висновки:
– якщо допустима сила і коефіцієнт тертя коченні зі зміною відношення модуля пружності рейки E2 до колеса E1 збільшується практично лінійно, то відповідна силі величина опору руху колеса W збільшується нелінійно з тенденцією більш швиlкого зростання, а величина відносного опору руху W/Р теж збільшується, але з тенденцією зменшення;
– опору кочення циліндра радіусом R і довжино В можна досягти рівнем опору ковзання, наприrлад, пластини розміром В×L, при отриманих відношеннях між L і f; цієї ж рівності можна досягти і для кулі, і для пластини.
Бібліографічний список
1. Tabor D. The mechanism of rolling friction: the elastic range. Proc. Roy. Soc. Ser. A. – 1995. – V. 229. – P. 198 – 211.
2. Бондаренко Л.Н. Экспериментально–аналитическое определение коэффициента трения качения Зб. наук. праць ХарДАЗТ, 1999. – Вип. 36. – С. 127 – 132.
3. Смирнов Г.Ф., Бондаренко Л.Н. Аналитическое определение КПД канатных полиспастов // Изв. ТулГУ, 1999. – Вып. 2. – С. 126 – 130.
4. Ловейкин B.C., Бондаренко Л.Н. Аналитическое представление коэффициента сопротивления и величины гистерезисных потерь при качении // Техніка будівництва. – 2000. – № 7. – С. 45 – 48.