Проблема и ее связь с научными и практическими задачами. Безаварийная эксплуатация подъемной машины при беспрерывно возрастающих технических показателях может быть обеспечена лишь при гармоничном сочетании всех ее параметров на основе учета в тяжело нагруженных элементах, вызванных периодически изменяющимися или повторяющимися силовыми факторами .Одним из основных элементов шахтной подъемной машины (ШПМ) являются опорные узлы, фиксирующие положение коренного вала и обеспечивающие его вращение. Их состояние во многом определяет срок службы всей машины. Существующая система планово – предупредительного ремонта (ППР) обладает обобщенными способами и средствами определения технического состояния. Для нормальной эксплуатации ШПМ необходимо применять систему непрерывного мониторинга и анализа комплекса диагностических параметров, однозначно определяющих дефекты в опорных узлах. К таким параметрам относятся вибродиагностические параметры: виброперемещение; виброскорость; виброускорение. Состояние опорных узлов во многом зависит от динамических нагрузок, но и они, в свою очередь, влияют на динамические процессы, происходящие в подъемных машинах .такого рода взаимосвязанные динамические процессы отличаются достаточно большим разнообразием, зависящим от типа машин и соотношения параметров всей подъемной системы. Исследованием этих процессов занимались многие ученые, применяя различные подходы и модели, получая при этом ту или иную точность и степень обобщенности. Но до настоящего времени отсутствует приемлемый для практического применения метод расчета фактических сил динамического воздействия на опорные узлы коренного вала. .
Анализ исследований и публикаций. Вопросами динамики подъемных машин занимались Г.Н. Савин, О.А. Горошко, Н.Г. Гаркуша, В.И. Белобров, В.И. Самуся, С.Р. Ильин. Значительный вклад в разработку динамики внесли В.И. Дворников и его ученики. Исходя из принятых ими рабочих гипотез, подъемная машина представляется как система пяти дискретных масс. Выведены дифференциальные уравнения динамического состояния этой механической системы.
Постановка задач.LЦелью является разработка математической модели многоканатной подъемной установки и определение неблагоприятных сочетаний параметров, вызывающих неустойчивое вращение коренного вала и нахождение границы области устойчивых движений.
Изложение материала и результаты.То обстоятельство, что при работе машины подшипниковые узлы коренного вала находятся в довольно интенсивном вибрационном состоянии, является экспериментальным фактом, проверенным и подтвержденным многочисленными приборными измерениями. Это свидетельствует о податливости подшипниковых опор машины. Будем считать такое утверждение первой посылкой, принятой в основу разрабатываемой математической модели.
Вместе с тем, вибрации подшипниковых опор ротора электродвигателя сравнительно мала, если делать оценку по измеряемым амплитудам виброскорости. Объясняется это тем, что, во-первых, наличие в трансмиссии машины специальной зубчатой муфты со сферической кромкой зубьев шестерни, приводят к тому, что в данном случае муфта является эффективным виброизолятором. Во-вторых, на ротор двигателя в поперечном направлении, кроме его собственного веса, не действуют никакие нагрузки, тем более, вибрационного характера. Это является второй посылкой.
А так как в силу кинематики зацепления исключается любая возможность малых радиальных смещений шестерни относительно венца даже при наличии регламентируемых боковых зазоров в зацеплении, то, в целом, коренной вал машины вместе с барабаном, используя терминологию классической механики, можно уподобить волчку с неподвижной точкой в полумуфте этого вала. Это будет третьей посылкой.[1]
Математическое описание движения вала машины с барабаном, основывается на представлении, что вал машины подобен «волчку» с одной неподвижной точкой.
Коренной вал машины опирается на податливые опоры подшипников в точках А и В, а вал ротора на недеформируемые опоры в точках С и D.

Опоры вала в точках A и B имеют коэффициенты жесткости Cx и Cy соответственно направлениям осей координат.
Силы G'Б= GБ/2
где GБ – вес барабана машины, поровну распределенный на две ступицы в точках A',B'.Сила GБ – вес коренного вала, который предполагается сосредоточенным в точке o', являющейся серединой пролета AB.
Силы Pxk и Pyk (k=1,2,... n) - проекции на соответствующие оси суммарных усилий в набегающей и сбегающей ветвях k-го каната при общем их количестве, равном n. Силы Fx1, Fx2, Fy1, Fy2 являются проекциями сил воздействия соответствующих ступиц на коренной вал в точках A', B'.



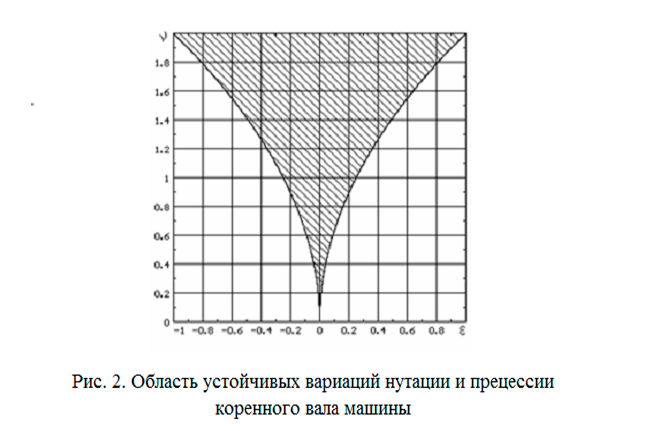
Решение системы уравнений (7) относительно функций σβ позволяет определить динамические вариации нутации и прецессии вала, что в итоге приводит к построению областей устойчивых решений системы (7) в поле технически реализуемых значений параметров ν и ε, что дает возможность на практике отстраиваться от неблагоприятных и опасных режимов движения. На рис. 2. в координатах ν и ε построены границы области устойчивых движений рассматриваемой системы (заштрихованная область). Как видно, область устойчивости является практически симметричной относительно алгебраической величины дисторсионного параметра ε. [2]
Расчет областей устойчивых вариаций нутации и прецессии коренного вала машины выполнены для подъемной машины ЦШ 5х4 ОАО «Угольная компания «Шахта Красноармейская - Западная №1»
Выводы и направления дальнейших исследований. В данной статье приведена математическая модель подъемной машины с упругими подшипниковыми связями. Она легла в основу разработанного программного модуля определения динамических нагрузок на опоры коренного вала шахтных подъемных машин. С помощью разработанного программного модуля можем для новых подъемных машин, а также находящихся в эксплуатации строить зоны устойчивых вариаций прецессии и нутации коренного вала и таким образом избегать нежелательных параметрических колебаний.
Список литературы
1 Белобров В.И. Динамика шахтных подъемных установок /В.И. Белобров, В.И. Самуся, С.Р. Ильин // Издательство Днепропетровского университета. -2000. – 384 с.
2 Бежок В.Р. Шахтный подъем / В.Р. Бежок, В.И. Дворников, И.Г. Манец, В.А. Пристром // Юго–Восток ЛТД. - 2007. – 624 с
3 Дворников В.И. Уравнение динамики коренного вала шахтной подъемной машины /В.И. Дворников, В.А. Яценко // Сборник научных трудов «Вести Донецкого горного института». – 2006. - №1. - С. 139 – 143.
4 Дворников В.И. Создание математической модели силовых факторов, действующих на вал подъемной машины / В.И. Дворников, В.А. Яценко // Наукові праці ДНТУ. Серія: «Гірничо – електромеханічна». – 2006. - Вип. 12. - С. 99 -104.
Рецензент: канд. техн. наук, проф. Л.М. Козиряцький