Генератор самоподобного трафика для моделей информационных сетей.

Бессараб В.И., Игнатенко Е. Г.,Червинский В. В.

Интернет доступ: http://archive.nbuv.gov.ua/portal/soc_gum/vsunu/2010_2/Bessarab.pdf

В статье проведено исследование свойств реального трафика в современных сетях с пакетной коммутацией. С использованием метода R/S анализа показана самоподобная природа сетевого трафика в информационных сетях. Разработана математическая модель генератора трафика, отражающая мультифрактальное поведение потоков данных в реальных информационных системах, позволяющая имитировать трафик с заданными показателями самоподобия. Рис. 4, табл. 3, ист. 10.

Ключевые слова: релаксация лагранжа, система управления, автоматизация, оптимальное управление, дискретно- непрерывная система, критерий оптимальности

Исследования характеристик сетевого трафика в современных сетях показывают, что для сетей с пакетной коммутацией трафик является самоподобным (self-similar) или фрактальным по своей природе. В нем присутствуют так называемые вспышки или пачки пакетов, наблюдаемые в различных временных интервалах (от милисекунд до минут или даже часов) [1]. Классическими работами в области анализа процессов в информационных сетях на предмет самоподобия являются [2-5].

Доказано, что широко используемые в настоящее время методы моделирования и расчета сетевых систем, основанные на использовании пуассоновских потоков, не дают полной и точной картины происходящего в сетях с пакетной коммутацией.

В качестве необходимости реализаций генераторов самоподобного трафика можно привести в пример работы [6-7]. Так, в работе А. Г. Ложковского [6] создана имитационная модель одноканальной системы обслуживания самоподобного трафика, исследовано влияние характеристик самоподобного трафика на пропускную способность системы. В работе Г. А. Кучук [7] показано, что использование классического распределения Парето при моделировании трафика изолированного пульсирующего источника с долговременной зависимостью позволяет учесть фрактальный характер трафика. Для более точной аппроксимации трафика по имеющимся статистическим данным необходимо использовать alfa-устойчивое распределение с соответствующими параметрами, оценку адекватности которого можно произвести с использованием соответствующей статистики.

Целью работы является разработка математической модели генератора трафика, отражающей мультифрактальное поведение потоков данных в реальных информационных системах (с различными степенями самоподобия) и позволяющая учитывать влияние различных типов запросов на загрузку системы (определяемое средним временем обслуживания).

Самоподобные процессы, в отличие от пуассоновских, характеризуются наличием последействия, т.е. вероятность поступления следующего события зависит не только от времени, но и от предыдущих значений событий. Это означает, что число текущих событий может зависеть от предыдущих событий в отдаленные промежутки времени. Именно поэтому одним из основных свойств самоподобного процесса является МУЗ – медленно убывающая зависимость. Важным параметром, характеризующим степень самоподобия, является параметр Херста H.

С учетом показателя Херста выделяют три типа случайных процессов:

1. 0 < H < 0.5 – случайный процесс, который не обладает самоподобием;
2. H = 0.5 – полностью случайный ряд, аналогичный случайным смещениям при классическом броуновском движении частицы;
3. H > 0.5 – самоподдерживающийся процесс, который обладает длительной памятью и является самоподобным.

Также стоит отметить, что самоподобный процесс часто носит «взрывной» характер, который выражается в возможности наличия выбросов при относительно низкой скорости поступления событий.

Применительно к теории телетрафика самоподобие выражается в неизменности поведения потока при изменении временных масштабов наблюдения и сохранении склонности к всплескам при усреднении по шкале времени.

Статистические данные времени поступления запроса для работы были получены экспериментально и обработаны с помощью Multi Router Traffic Grapher (MRTG). Схема эксперимента приведена на рис. 1:

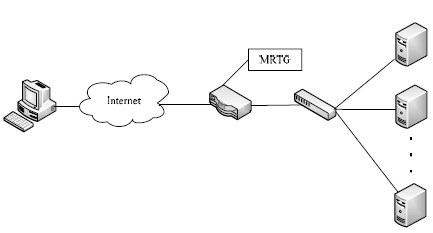
Рис. 1. Схема получения статистических данных

Для исходной реализации трафика проведена процедура агрегирования с уровнем агрегирования dT = 0,05 сек.; которая заключается в разделении всего временного интервала на промежутки длиной dT. На рис. 1 представлен график агрегированной реализации трафика на заданных интервалах (по оси ОХ – № интервала длиною 0,05 сек., по оси ОУ – количество http-запросов запр/инт):

Из приведенного графика видно, что наблюдаемый процесс неравномерный, и соответствует описанным выше признакам самоподобных процессов – наблюдается масштабная инвариантность, наличие всплесков, МО остается почти неизменным и относительно малым в сравнении с максимальными выбросами. Именно такой вид процесса можно описать распределением Парето, характеризующимся «тяжелыми хвостами».

В ходе исследования трафика доказано, что данная реализация не соответствует пуассоновскому распределению, т.к. не выполняется условие равенства математического ожидания M = 8,57377 и дисперсии D = 75,8153 для распределения количества моментов поступления пакетов, попавших в последовательность временных интервалов заданной длины.

Рис. 2. График реализации трафика, агрегированной по уровню 0,05

Основной характеристикой рядов, обладающих хаотическим поведением, является, как известно, показатель Херста [8]. Для его определения применяется так называемый R/S-анализ, который широко используется в исследованиях фрактальной природы информационных потоков [9]. Он позволяет достаточно эффективно исследовать свойства числовых рядов на основе отношения разброса значений к среднеквадратичному отклонению.

Пусть R – размах значений числового ряда; n – набор значений ряда наблюдений; S – его среднеквадратичное отклонение. Тогда имеет место соотношение:

где H – показатель Херста.

Для исследуемой реализации трафика с помощью R/S-анализа определено значение показателя Херста: H = 0,647. Для проверки значение параметра Херста также получено методом модифицированной дисперсии Аллана: H = 0,645. Данное значение попадает в интервал 0,5 < H < 1, следовательно, подтверждается гипотеза о самоподобии исследуемого трафика.

На основании вышесказанного проведено моделирование процесса поступления запросов на обслуживание, где промежуток между вызовами описывается распределением Парето, а время обслуживания – экспоненциальным распределением.

Процесс поступления в систему запросов на обслуживание моделируется как рекуррентный, где момент поступления следующего запроса получается путем прибавления случайного интервала времени к предыдущему. Случайные интервалы между заявками формируются по распределению Парето, которое при моделировании получается путем перехода от равномерного распределения методом обратных функций [10]:

де Zi – i-й промежуток времени между заявками; – параметр формы распределения; b – мода распределения, r– случайное число, равномерно распределенное на промежутке [0,1]. Т.к. при <2.5 дисперсия бесконечна, то именно это распределение с бесконечной дисперсией и «длинным хвостом», которым и является распределение Парето, позволяет моделировать потоки трафика с эффектом самоподобия. Время обслуживания распределено по экспоненциальному закону:

где hk – среднее время обслуживания для k -ого типа запроса (напр., см. Табл. 2), r– случайное число, равномерно распределенное на промежутке [0,1].

Т.к. последовательность http-запросов содержит в себе различные типы запросов, которые встречаются с разной частотой и требуют разного времени обслуживания, то необходимо учитывать этот факт при моделировании. http-запрос – это сообщение, посылаемое клиентом серверу. Тип http-запроса (также называемый http-метод) указывает серверу на то, какое действие необходимо произвести с ресурсом. Изначально предполагалось, что клиент может требовать от ресурса только одно – получить его, однако сейчас по протоколу http можно создавать посты, редактировать профиль, удалять сообщения и многое другое.

Для разграничения действий с ресурсами на уровне http-методов предложены такие варианты их классификации:

• get – используется для запроса содержимого указанного ресурса.
• head – аналогичен методу get, за исключением того, что в ответе сервера отсутствует тело. Запрос head обычно применяется для извлечения метаданных, проверки наличия ресурса (валидация URL) и чтобы узнать, не изменился ли он с момента последнего обращения.
• post – применяется для передачи пользовательских данных заданному ресурсу. При этом передаваемые данные включаются в тело запроса. Аналогично с помощью метода post обычно загружаются файлы.
• put – применяется для загрузки содержимого запроса на указанный в запросе URI. Используя put, клиент предполагает, что загружаемое содержимое соответствует находящемуся по данному URI ресурсу.
• delete – удаляет указанный ресурс.
• и другие.

В ходе статистического анализа http кодов по методам получена информация, представленная в табл. 1:

Таблица 1

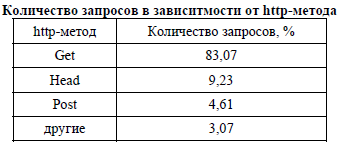
Таким образом, можно сделать вывод, что http определены три основных метода: get, head и post. Определены и другие методы, но они не так широко поддерживаются серверами.

В соответствии с вышесказанным в среде программирования NetBeans разработана программа имитационного моделирования системы обслуживания потока http-запросов. В программе предусмотрено 2 генератора случайных величин для задания промежутка между запросами и времени обслуживания запроса, с возможностью задания всех необходимых вероятностно-временных характеристик этих величин. Например, продолжительность обслуживания запросов может быть распределена по экспоненциальному, равномерному и нормальному законам. Также в модели учтен метод запроса по http-коду и соответствующее ему время обслуживания.

Рис.3. Очередность поступления http-запросов в зависимости от типа для выборки n=100

Для проверки полученной модели смоделируем поток запросов с параметрами: b = 0,001 c ; alfa = 1,706 ; H = 0,647 . Эти параметры соответствуют экспериментальной реализации трафика, рассмотренной выше. Время обслуживания запросов распределено по экспоненциальному закону, и для каждого типа http-запроса задано среднее время обслуживания. Результаты представлены в табл. 2.

Графическая форма результатов моделирования приведена на рис. 3:

Таблица 2

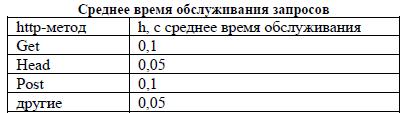
Статистическая обработка результатов моделирования приведена на рис. 4:

Рис. 4. Количество запросов, попавших в интервал (по оси Х–№интервала, по оси У– количество запросов, запр/инт)

Проверка, является ли полученный таким образом поток самоподобным с заданными параметрами, показывает, что значение показателя Херста для смоделированного потока запросов, определенное с помощью R/S-анализа: H = 0,652 Т.е. значение принадлежит интервалу 0,5 < H < 1 , следовательно, данная реализация имеет самоподобный характер. Сравним заданные и смоделированные параметры, для этого сведем данные в табл. 3:

Таблица 3

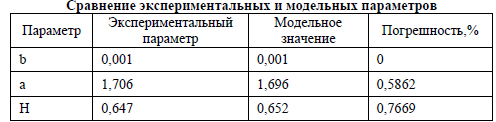
Значения модельных параметров соответствуют полученным в ходе измерения реального трафика сервера в сети. Это позволяет использовать разработанную модель для исследования реальных информационных систем.

Для генерации самоподобного трафика с заданным параметром Херста можно воспользоваться таким выражением, связывающем параметр Херста и параметр формы распределения [7]:

Результаты моделирования времени обслуживания запросов могут быть использованы для анализа работы СМО, в частности для web-кластера серверов.

Выводы. На основании данных, полученных в ходе экспериментов, доказана самоподобная природа реального сетевого трафика информационных сетей. Предложена модель, которая описывает самоподобный трафик с различными степенями самоподобия. Разработана модель обслуживания самоподобного трафика, где в качестве источника используется предложенный генератор. Для изучения функционирования информационных систем в условиях самоподобного трафика разработаны специальный алгоритм и программа, позволяющие моделировать самоподобный трафик. Предложенный подход к моделированию может быть использован для моделей сетей сложной топологии.

Литература

1. Заборовский В. С. Методы и средства исследования процессов в высокоскоростных компьютерных сетях [Текст]: Дис. д-ра техн. наук : 05.13.01. / Зарабовский Владимир Сергеевич – СПб., 1999. – 268 с., Библиограф.: с. 256-268. – Санкт- Петербургский государственный технический университет.
2. Городецкий А. Я., Заборовский В. С. Информатика. Фрактальные процессы в компьютерных сетях: Учебное пособие. – СПб.: изд-во СПбГТУ, 2000 – 102 с.
3. Морозов А. Д. Введение в теорию фракталов – М.: Институт компьютерных исследований, 2002. – 159 с.
4. Кроновер Р. М. Фракталы и хаос в динамических системах – М.: Постмаркет, 2000. – 352 с.
5. Столлингс В. Современные компьютерные сети. – 2-е изд. – СПб: Питер, 2003 – 784 с.
6. Ложковський А.Г., к.т.н., доц.; Нікіфоренко К.Б. Дослідження функціонування телекомунікаційних систем в умовах само подібного трафіка. Управління мережами і послугами телекомунікацій – Наукові записки УНДІЗ, №2(10), 2009.
7. Кучук Г.А. Учет фрактальных свойств пульсирующего трафика. Материалы I Международной научно-технической конференции "Инфотелекоммуникационные технологии в науке, производстве и образовании", Северо-Кавказский государственный технический университет, 2007.
8. Федер Е. Фракталы. – М.: Мир, 1991. – 254 с.
9. Ландэ Д.В. Фрактальные свойства тематических информацийнных потоков из Интернет // Реєстрація, зберігання і оброб. даних. – 2006. – Т. 8, № 2. – С. 93–99.
10. Шнепс М.А. Системы распределения информации. Методы расчета: справ. пособие. – М.: Связь, 1979. – 344 с.

Аннотации

У статті наведено дослідження властивостей реального трафіка в сучасних мережах з пакетною комутацією. З використанням методу r/s аналізу показана самоподібна природа мережного трафіка в інформаційних мережах. Розроблена математична модель генератора трафіка, що відображає мультифрактальну поведінку потоків даних у реальних інформаційних системах, яка дозволяє імітувати трафік із заданими показниками самоподібності.

Ключові слова: релаксація лагранжа, система управління, автоматизація, оптимальне управління, дискретно- безперервна система, критерій оптимальності

This article is intended to show the characteristics of real traffic in modern packet-switched networks. Self-similar nature of network traffic was proved through R/S analysis method. Math-model of traffic generator was developed. It involves multifractional behaviour of traffic-flows in real informational systems. This model lets us emmulate traffic with defined self-similarity keycharacteristics.

Keywords: lagrange relaxation, control system, automation, optimal control, discrete-event system, optimality criterion

Сведения об авторах

Бессараб В. И. – к.т.н., доц., зав. кафедрой автоматики и телекоммуникаций Донецкого национального технического университета

Игнатенко Е. Г. – аспирант кафедры автоматики и телекоммуникаций Донецкого национального технического университета