Надежные условия устойчивости при переменном периоде дискретности
Автор: M.C. de Oliveiraa, J.
Bernussoub, J.C. Geromela;.
Перевол: Борейко О.В.
Автор: M.C. de Oliveiraa, J.
Bernussoub, J.C. Geromela;.
Перевол: Борейко О.В.
Дословно термин "робастное управление" означает "сильное управление", т.е. управление с определенным запасом, например, по устойчивости. Практическая ценность задачи робастного управления связана с тем, что синтезированная по критериям устойчивости система управления может иметь малую чувствительность к изменению параметров или большую. В первом случае говорят о грубости системы или о ее робастности, во втором случае система практически неработоспособна, так как малейший уход параметров ведет к потере устойчивости. Таким образом, постановка задачи робастного управления связана с требованием сохранения работоспособности системы при наличии неопределенностей в ее описании.
В робастном управлении рассматриваются два вида неопределённостей — структурные и неструктурные. Неструктурные неопределённости делятся на аддитивные и мультипликативные обычно представляют собой элементы, зависящие от частоты, такие как, например, насыщение в силовых приводах или возмущения в низкочастотной области АФЧХ объекта управления..
Данная статья посвящена анализу метода робастной устойчивости при котором каждый член матрицы является множеством асимптотически устойчивым в дискретный момент времени. В работе используется метод Ляпунова.
Анализ проблемы:
Пусть дискретная система с неопределенностью описывается уравнением:
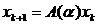 (1.3)
(1.3)
где
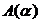 -
матрица динамики
-
матрица динамики
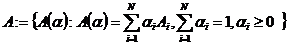 (1.4)
(1.4)
Определение
1: Система (1.3) стабильна в области
неопределенности (1.4) если все собственные значения матрицы
, имеют величину меньше 1 для всех значений ![]() таких
что
.
таких
что
.
Воспользовавшись определением устойчивости по Ляпунову, можно преобразовать определение 1 в эквивалентное условие приведенное в лемме 1.
Лемма 1: система (1.3) стабильна в области неопределенности (1.4) тогда, когда выходы матрицы такие что:
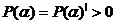 (1.5)
(1.5)
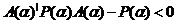 (1.6)
(1.6)
На данный момент
не существует способа формально
определить
, как функцию от неопределенного параметра ![]() .
Матрица
является
зависимой от параметров матрицы Ляпунова. Матрицу удовлетворяющую
условию
заданному в Лемме 1 можно найти с использованием ЛМН. Это можно
реализовать с
помощью Леммы 2.
.
Матрица
является
зависимой от параметров матрицы Ляпунова. Матрицу удовлетворяющую
условию
заданному в Лемме 1 можно найти с использованием ЛМН. Это можно
реализовать с
помощью Леммы 2.
Лемма 2: Система с неопределенностью (1.3) является стабильной в области неопределенности (1.4) если:
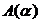 (1.7)
(1.7)
Теорема 1:
Условия эквивалентности (1): существует ![]() симметричная
матрице
симметричная
матрице ![]() .
Такая что:
.
Такая что:
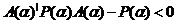 (1.8)
(1.8)
Условие
эквивалентности (2): Существует симметричная
матрица ![]() и
матрица
и
матрица ![]() такие
что:
такие
что:
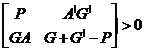 (1.9)
(1.9)
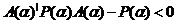 (1.4)
(1.4)
Определение
1: Система (1.3) стабильна в области
неопределенности (1.4) если все собственные значения матрицы
, имеют величину меньше 1 для всех значений ![]() таких
что
.
таких
что
.
Воспользовавшись определением устойчивости по Ляпунову, можно преобразовать определение 1 в эквивалентное условие приведенное в лемме 1.
Лемма 1: система (1.3) стабильна в области неопределенности (1.4) тогда, когда выходы матрицы такие что:
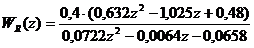 (1.5)
(1.5)
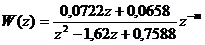 (1.6)
(1.6)
На данный момент
не существует способа формально
определить
, как функцию от неопределенного параметра ![]() .
Матрица
является
зависимой от параметров матрицы Ляпунова. Матрицу удовлетворяющую
условию
заданному в Лемме 1 можно найти с использованием ЛМН. Это можно
реализовать с
помощью Леммы 2.
.
Матрица
является
зависимой от параметров матрицы Ляпунова. Матрицу удовлетворяющую
условию
заданному в Лемме 1 можно найти с использованием ЛМН. Это можно
реализовать с
помощью Леммы 2.
Лемма 2: Система с неопределенностью (1.3) является стабильной в области неопределенности (1.4) если:
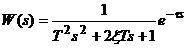 (1.7)
(1.7)
Теорема 1: Условия эквивалентности (1): существует симметричная матрице . Такая что:
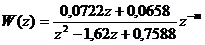 (1.8)
(1.8)
Условие эквивалентности (2): Существует симметричная матрица и матрица такие что:
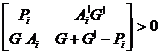 (1.9)
(1.9)
Доказательство:
применим дополнение Шура к матрице
(1.9) и восстановим (1.8) выбрав 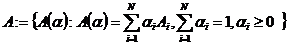 .
Следовательно (1) условие эквивалентности следует из
(2). С другой стороны, если в (1.9)
. Тогда умножив (1.9) на
слева и на
справа мы получим (1.8). Следовательно (2) условие
эквивалентности вытекает из (1).
.
Следовательно (1) условие эквивалентности следует из
(2). С другой стороны, если в (1.9)
. Тогда умножив (1.9) на
слева и на
справа мы получим (1.8). Следовательно (2) условие
эквивалентности вытекает из (1).
Условие (2) является расширение условия (1). Дополнение Шура позволяет нам ввести матрицу чтобы получить линейно матричные неравенства в которых матрица Ляпунова не участвует в уравнениях с динамической матрицей . Эта функция позволяет нам получить новые условия робастной устойчивости не являющиеся сильно консервативными за счет наличия дополнительной степени свободы путем введения матрицы . Дополнительная матрица не обязательно должна быть симметричной.
Теорема 2: система с неопределенностью (1) является стабильной в области неопределенности (2) если существует симметричная матрица матрице такая что:
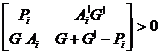 (1.10)
(1.10)
Следуя по той же схеме как и при доказательстве теоремы 1, покажем что если условие (1.9) выполняется то существуют выходы зависящие от параметров матрицы Ляпунова.
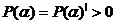 (1.11)
(1.11)
Матрица положительно определенна для всех значений где . Таким образом определение возможных матриц и может быть легко реализовано с помощью решений для линейно матричных неравенств (ЛМН).
Рассмотрим линейную дискретную систему:
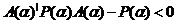 (1.12)
(1.12)
Где матрица динамики принадлежит как указано в (1.2) и определен как указано ниже.
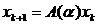 (1.13)
(1.13)
Мы ищем усиление обратной связи такое что асимптотически устойчива для каждого
Теорема 3: Система с неопределенностью (1.10) устойчива в области неопределенности (1.4) и (1.11) если существуют симметричные матрицы и матрица такие что:
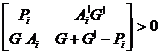 (1.12)
(1.12)
для каждого
В (1.12) обратная связь задается:
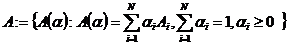 (1.13)
(1.13)
Доказательство.
Теорема 3 доказывается с помощью транспонирования теоремы 2 путем
транспонирования ![]() и
и
![]() ,
вместе с изменением переменных
. Примем
,
вместе с изменением переменных
. Примем 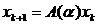 .
.
Следовательно
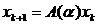 (1.14)
(1.14)
Был изложен достаточное условие робастной устойчивости дискретных систем с неопределенностью.
Как следует из вышеизложенного, робастный регулятор гарантирует устойчивость замкнутой системы управления, если неизменяемая во времени параметрическая или неизменяемая по времени структурная неопределенность принадлежит некоторому множеству. Вместе с тем, условия робастности не гарантируют устойчивости замкнутой системы управления даже при достаточно малых параметрических или структурных изменениях во времени. Эту задачу решает теория абсолютной устойчивости.
Перечень ссылок
1. D.-W. Gu, P. Hr. Petkov and M. M. Konstantinov. Robust Control Design
with MATLAB.
2.R.J. Adams, J.M Buffington, A.G. Sparks, and S.S. Banda. Robust Multivariable
Flight Control. Springer-Verlag, New York, 1994.
3. U.M. Al-Saggaf and G.F. Franklin. An error bound for a discrete reduced
order model of a linear multivariable system. IEEE Transactions on Automatic
Control, AC-32:815–819, 1987.
4. G.J. Balas, J.C. Doyle, K. Glover, A. Packard, and R. Smith. μ-Analysis and
Synthesis Toolbox: User’s Guide. MUSYN Inc. and The Mathworks, Inc., 1995.
5. D.S. Bernstein and W.M. Haddad. LQG control with an H∞
performance
bound: A Riccati equation approach. IEEE Transactions on Automatic Control,
AC-34:293–305, 1989.