Аннотация
Вовна А.В., Дробот А.А. Разработка математической модели измерительного контроля концентрации пыли в газах теплоэлектростанции. Промоделирован процесс рассеяния оптического излучения частицей пыли. Построена градуировочная характеристика измерителя.
Общая постановка проблемы
Образование и выброс пыли сопровождает большинство технологических процессов, таких, как: сжигание мусора и опасных отходов, производство цемента, стекольная, бумажная и коксохимическая промышленности.
Основной параметр, характеризующий состояние аэродисперсных систем в различных отраслях промышленности – концентрация частиц в технологических газах, загрязняющих атмосферу. Диаметр частиц в источниках выбросов различных производств составляет от 0,1 до 120 мкм при их концентрации от 0,3 мг/м3 до 150 г/м3.
Основными средствами улавливания пыли являются рукавные и электростатические фильтры, снижение эффективной работы которых приводит к ощутимым финансовым потерям. Поэтому, экологический мониторинг и контроль эффективности фильтров является актуальной задачей.
Постановка задач исследования.
Для достижения цели поставлены и решены следующие задачи:
– разработать и исследовать математическую модель измерительного контроля концентрации пыли в газах ТЭС;
– поставить требования к разработке макетного образца измерительного прибора контроля концентрации пыли.
Результаты разработки и исследований.
Из проведенного анализа методов и средств измерений следует, что наиболее подходящими методами измерительного контроля концентрации пыли являются оптические методы. Эти методы просты в применении, обеспечивают малую погрешность и дают возможность контроля концентрации пыли в реальном масштабе времени как с пробоотбором, так и без. Суммарная интенсивность рассеянного света существенно зависит от параметра 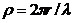 . Можно выделить три основные граничные значения этого параметра: р<<1, р=1, р>>1.
. Можно выделить три основные граничные значения этого параметра: р<<1, р=1, р>>1.
В случае р<<1 размеры частиц малы в сравнении с длиной волны и рассеивание света сферической частицей с радиусом r из диэлектрика для неполяризованного света описывает-ся уравнением Релея:
где 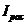 – интенсивность света, рассеянного под углом к падающему потоку, рассчитанная на единицу интенсивности падающего света, мВт; R – расстояние от точки наблюдения до частицы, м;
– интенсивность света, рассеянного под углом к падающему потоку, рассчитанная на единицу интенсивности падающего света, мВт; R – расстояние от точки наблюдения до частицы, м; 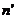 – комплексный коэффициент преломления частицы; r – радиус частицы, мкм;
– комплексный коэффициент преломления частицы; r – радиус частицы, мкм; 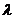 – длина волны излучения, мкм. В этом случае индикатриса рассеяния симметрична, а интенсивности рассеянного вперёд и назад излучения одинаковы.
– длина волны излучения, мкм. В этом случае индикатриса рассеяния симметрична, а интенсивности рассеянного вперёд и назад излучения одинаковы.
При р>>1размеры частиц значительно больше длины волны. Этот случай описывается законом Бугера-Ламберта-Бера:
где, Iп, I0 – интенсивности поглощённого и зондирующего излучений, мВт; k – спектральный коэффициент поглощения; С – концентрация; L – толщина поглощающего слоя газа, м. Эта формула справедлива для поглощения средой зондирующего излучения только в условиях монохроматичности излучения, независимости коэффициента поглощения от частоты и кон-центрации поглощающих частиц.
Если р=1, размеры частиц соизмеримы с длиной волны. Зависимость между интенсив-ностью рассеянного света, размером частиц и длиной волны определяется уравнением Ми:
где, Iрас - интенсивность света, рассеянного под углом к падающему потоку, рассчитанная на единицу интенсивности падающего света, мВт; R – расстояние от точки наблюде-ния до частицы, м; 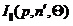 и
и 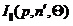 - интенсивность рассеянного света, поляризованного перпендикулярно и параллельно плоскости рассеяния, мВт. В этом случае индикатриса рассеяния усложняется, по сравнению с Релеевской, и увеличивается рассеяние вперёд.
- интенсивность рассеянного света, поляризованного перпендикулярно и параллельно плоскости рассеяния, мВт. В этом случае индикатриса рассеяния усложняется, по сравнению с Релеевской, и увеличивается рассеяние вперёд.
На рис.1 изображена структура математической модели измерительного контроля концентрации пыли. На схеме изображено: СИД – светоизлучающий диод; ФП – фотопри-ёмник. Для пылегазовой среды задаются следующие параметры: дисперсный состав (закон распределения частиц по размерам); С – концентрация пыли. СИД формирует зондирующее излучение с конкретной длиной волны в пылегазовую среду. ФП регистрирует рассеянное излучение. Так же на схеме указаны дестабилизирующий фактор – температура среды. Температура влияет как на концентрацию, так и на спектральные характеристики излучателя, изменяя его центральную длину волны и интенсивность излучения.
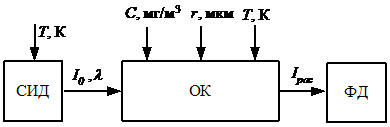
Рисунок 1 – Структура модели измерительного преобразования потока излучения
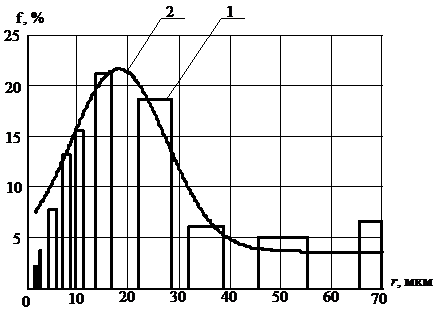
Рисунок 2 – Дисперсный состав пыли
1 – аналитическая зависимость, 2 – аппроксимирующая кривая
Дисперсный состав пыли (см. рис. 2) [5] был аппроксимирован следующей зависимо-стью:
где r – радиус частиц имеющих максимальное количество в распределении, мкм; a – дисперсия закона распределения частиц по их радиусам, 1/мкм.
Из анализа зависимости (см. рис. 2) видно, что радиусы частиц промышленной пыли в основном находятся в диапазоне от 1,5 до 70 мкм, при этом наибольший процент массы частиц приходится на 15 мкм. Согласно [3], индикатриса рассеяния описывается формулой:
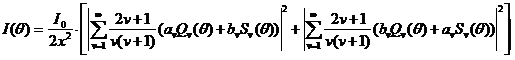
(1)
где 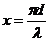 – параметр дифракции; I0 – интенсивность зондирующего излучения, мВт;
– параметр дифракции; I0 – интенсивность зондирующего излучения, мВт; 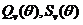 – угловые функции; a и b – коэффициенты Ми.
– угловые функции; a и b – коэффициенты Ми.
По формуле (1) получена индикатриса рассеяния для отдельной сферической частицы, позволяющая определить интенсивность рассеянного излучения в заданном направлении. Внешний вид индикатрисы представлен на рис 3. Для построения использовалась длина волны 0,642 мкм и радиус 15 мкм, т.е. радиус много больше длины волны. На индикатрисе явно отражается это соотношение увеличением интенсивности рассеяния частицей вперед. Для случая, когда длина волны больше радиуса частицы, интенсивность рассеянного вперёд и назад излучения становятся одинаковыми.
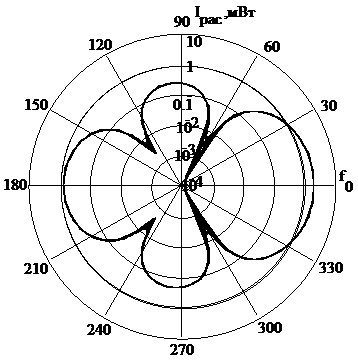
Рисунок 3 – Индикатриса рассеяния отдельной сферической частицы
Для некоторого множества частиц можно определить суммарную интенсивность рас-сеяния средой, а также построить градуировочную характеристику. Для построения градуировочной характеристики необходимо перевести концентрацию из мг/м3 в ppm, с учетом допущения, что частицы пыли находятся на достаточно большом расстоянии друг от друга, что сводит к минимуму их взаимное влияние, и среда является идеальным газом. Пересчет производится по формуле:
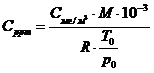
(2)
где 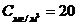 – концентрация (мг/м3); М – молярная масса вещества (углерод); R – газовая постоянная; T0, р0 – температура и давление при нормальных условиях (К) и (Па).
– концентрация (мг/м3); М – молярная масса вещества (углерод); R – газовая постоянная; T0, р0 – температура и давление при нормальных условиях (К) и (Па).
Для исходных данных с учетом (2) получим:
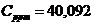
(3)
где С0 – концентрация пыли при нормальных условиях; Т и Р – отклонение температуры и давления от нормальных условий.
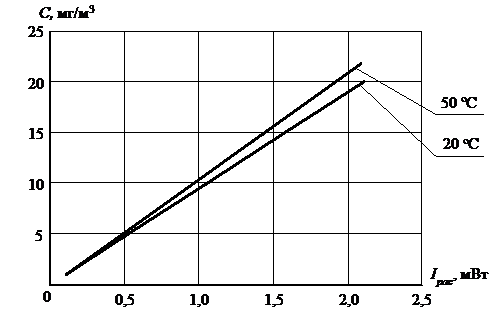
Рисунок 4 – Градуировочная характеристика измерительногоконтроля концентрации пыли
Градуировочная характеристика измерительного контроля концентрации пыли, которая получена с использованием (3) для температуры от 20 до 50 С, приведена на рис. 4.
Из анализа зависимости (см. рис. 4) видно, что характеристика линейна, а влияние тем-пературы носит мультипликативный характер и увеличивается к концу диапазона изме-рений. Это меняет угол наклона характеристики и чувствительность измерителя. По характеристике определена чувствительность для нормальных условий (Т=20 оС), величина которой составляет:
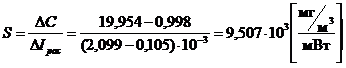
(4)
На основании проведенных исследований можно сделать вывод, что измеритель должен воспринимать излучение от 0,105 до 2,1 мВт и преобразовывать его к уровню вход-ного постоянного напряжения аналого-цифрового преобразователя величиной от 0 до 5 В.
Исходя из требований по распределению теории Ми, длина волны излучения должна быть меньше диаметра частицы. Отсюда, в качестве источника излучения выбран лазерный диод типа D6605I, со следующими характеристиками:
– центральная длина волны излучения: 0,66, мкм;
– номинальный ток питания: 12, мА;
– оптическая мощность: 5, мВт;
Излучение источника относится к красной области спектра, в диапазоне от 625 до 740 нм. Тогда, в качестве фотоприемника выбираем фотодиод, который воспринимает спектр как можно ближе к этой области, для уменьшения влияния остального спектра на результат измерения. Фотодиод типа ФД-20-30К перекрывает оранжевую и часть ИК-области. Его характеристики:
– диапазон длин волн 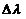 : от 0,5 до 1,1, мкм;
: от 0,5 до 1,1, мкм;
– напряжение питания 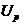 : 5, В;
: 5, В;
– темновой ток 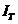 : 0,1, мкА;
: 0,1, мкА;
– интегральная чувствительность к сигналу 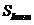 (при
(при 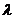 =0,9 мкм) : 0,3, А/Вт;
=0,9 мкм) : 0,3, А/Вт;
– постоянная времени 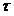 : 1,8, мкс.
: 1,8, мкс.
Выводы
При проведении исследований разработана математическая модель измерительного контроля концентрации пыли, которая учитывает индикатрису рассеяния отдельной сферической частицы с использованием математического аппарата теории Ми, что позволяет определить зависимость интенсивности рассеянного частицей излучения от угла рассеяния.
При исследовании математической модели получена градуировочная характеристика из-мерителя, которая имеет линейный характер на всём диапазоне концентраций от 0 до 20 мг/м3, что позволяет определить чувствительность измерителя по измерению концентрации пыли в указанном диапазоне.
Математическая модель учитывает влияние температуры на градуировочную характери-стику. Воздействие носит мультипликативный характер, изменяя угол наклона характери-стики, а, следовательно, чувствительность.
На основании результатов моделирования разработаны требования к измерителю:
Источник излучения был выбран исходя из требования Ми: длина волны должна быть меньше, по отношению к наименьшим частицам в дисперсном составе.
Фотоприёмник должен быть как можно более узкополосным. Его спектральная характе-ристика должна располагаться в красной области спектра. Это необходимо для снижения влияния фонового излучения.
Список использованной литературы
1. Клименко А.П. Методы и приборы для измерения концентрации пыли / А.П. Клименко, М.: Химия, 1978. – 198 с.
2. Справочник химика: в 6 т. Т. 4: Аналитический анализ, спектральный анализ, показатели преломления /Под. общ. ред. Б.П. Никольского. – Л.: Химия Ленингр. отделение. – 1967. – 920 с..
3. Галенко Ю.А. Моделирование коэффициента теплового излучения полубесконечной дисперсной среды / Ю.А. Галенко, М.О. Сысоева. // Ползуновский вестник. Алтайский государственный технический университет им. И.И. Ползунова. – № 1 – 2. – 2008. – С28 – 32.
4. Шифрин К.С. Рассеяние света в мутной среде. / К.С. Шифрин. – М. – Л.: Госттехиз-дат, 1951. – 288 с.
5. Штокман Е.А. Очистка воздуха. Учебное пособие. / Е.А. Штокман. – М.: Изд-во АСВ, 2007. – 312 с.
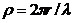 . Можно выделить три основные граничные значения этого параметра: р<<1, р=1, р>>1.
. Можно выделить три основные граничные значения этого параметра: р<<1, р=1, р>>1.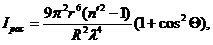
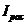 – интенсивность света, рассеянного под углом к падающему потоку, рассчитанная на единицу интенсивности падающего света, мВт; R – расстояние от точки наблюдения до частицы, м;
– интенсивность света, рассеянного под углом к падающему потоку, рассчитанная на единицу интенсивности падающего света, мВт; R – расстояние от точки наблюдения до частицы, м; 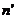 – комплексный коэффициент преломления частицы; r – радиус частицы, мкм;
– комплексный коэффициент преломления частицы; r – радиус частицы, мкм; 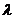 – длина волны излучения, мкм. В этом случае индикатриса рассеяния симметрична, а интенсивности рассеянного вперёд и назад излучения одинаковы.
– длина волны излучения, мкм. В этом случае индикатриса рассеяния симметрична, а интенсивности рассеянного вперёд и назад излучения одинаковы. 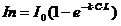
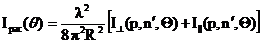
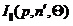 и
и 

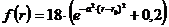
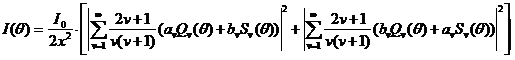 (1)
(1)
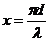 – параметр дифракции; I0 – интенсивность зондирующего излучения, мВт;
– параметр дифракции; I0 – интенсивность зондирующего излучения, мВт; 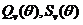 – угловые функции; a и b – коэффициенты Ми.
– угловые функции; a и b – коэффициенты Ми.
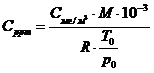 (2)
(2)
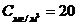 – концентрация (мг/м3); М – молярная масса вещества (углерод); R – газовая постоянная; T0, р0 – температура и давление при нормальных условиях (К) и (Па).
– концентрация (мг/м3); М – молярная масса вещества (углерод); R – газовая постоянная; T0, р0 – температура и давление при нормальных условиях (К) и (Па).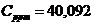 (3)
(3)

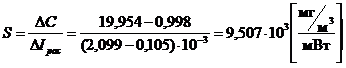 (4)
(4)
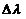 : от 0,5 до 1,1, мкм;
: от 0,5 до 1,1, мкм;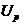 : 5, В;
: 5, В;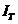 : 0,1, мкА;
: 0,1, мкА;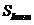 (при
(при 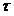 : 1,8, мкс.
: 1,8, мкс.