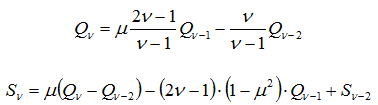Назад в библиотеку
ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ РАССЕЯНИЯ СВЕТА КАВИТАЦИОННОЙ ОБЛАСТЬЮ, ИНИЦИИРОВАННОЙ УЛЬТРАЗВУКОВЫМ ВОЗДЕЙСТВИЕМ
Автор:О.В. СТАРЫГИНА, Ю.А. ГАЛЕНКО, М.О. СЫСОЕВА
Источник: Галенко Ю.А. Моделирование коэффициента теплового излучения полубесконечной дисперсной среды / Ю.А. Галенко, М.О. Сысоева. // Ползуновский вестник. Алтайский государственный технический университет им. И.И. Ползунова. – № 1 – 2. – 2008. – С28 – 32.
Авторами выполнено численное исследование рассеяния оптического излучения кавитационной областью. В исследовании применялась модель распространения оптического излучения, основанная на решении уравнения переноса излучения в поглощающей и рассеивающей среде. Получены данные о зависимости коэффициента рассеяния от параметра дифракции, определены значения коэффициента рассеяния и вид индикатрисы рассеяния для типичных значений диаметра кавитационных пузырей. Полученные результаты могут использоваться при прогнозировании спектральных коэффициентов рассеяния и индикатрисы рассеяния, а также для выбора спектрального диапазона и метода экспериментальных исследований кавитационной области.
Акустические колебания достаточной интенсивности инициируют в жидкости кавитационный процесс. Диаметр образующихся кавитационных пузырей, их концентрация и характер изменения во времени в значительной мере определяют эффективность технологических процессов, выполняемых с применением ультразвука. Это является одной из причин повышенного внимания к исследованию кавитационной области.
В экспериментальных исследованиях широко применяются оптические методы, разработанные для дисперсных систем. В данном случае дисперсной средой является жидкость, а дисперсными частицами – кавитационные пузыри.
Целью нашей работы являлось определение спектрального коэффициента рассеяния оптического излучения и индикатрисы рассеяния для широких диапазонов длин волн и предполагаемых диаметров частиц.
Математическая модель излучения дисперсной системы основывается на решении уравнения переноса излучения в плоском слое поглощающей и рассеивающей среды.
В реализуемой модели для описания взаимодействия частиц с излучением используется теория Ми, а уравнение переноса излучения решается методом Д. Дейрменджана[1,2].
Исходными данными являются: диаметр частиц d и комплексные показатели преломления дисперсной среды и материала частиц 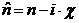 , где x - главный показатель поглощения материала, n - показатель преломления.
, где x - главный показатель поглощения материала, n - показатель преломления.
Результатами расчета являются спектральные коэффициенты (факторы эффективности) ослабления k, поглощения kпогл и рассеяния kрасс излучения частицами, а также индикатриса рассеяния.
Порядок расчетов следующий.
Первоначально вычисляется параметр дифракции для каждой длины волны по формуле
Затем рассчитываются коэффициенты Ми av и bv [1] для заданного числа парциальных волн v. Спектральные коэффициенты ослабления, рассеяния и поглощения излучения отдельной частицей рассчитываются в соответствии с теорией Ми по формулам
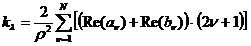
(1)
Подробно математическая модель и порядок расчетов описаны в работе [2]. Рассеяние излучения предполагалось однократным.
На рисунках 1, 2, 3 приведены полученные результаты.
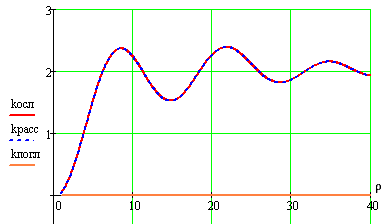
Рисунок 1 – Ослабление оптического излучения кавитационным пузырем в зависимости от параметра дифракции p
С использованием этих результатов можно оценить коэффициент рассеяния кавитационного пузыря при прогнозируемых значениях диаметра пузыря и длины волны зондирующего излучения.
Вид зависимости коэффициента рассеяния от длины волны для двух значений диаметра кавитационного пузыря d иллюстрирует рисунок 2.
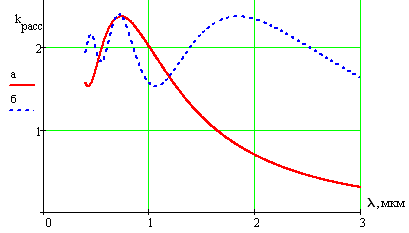
Рисунок 2 – Рассеяние излучения кавитационным пузырем в зависимости от длины волны для d=5 мкм (а) и d=2 мкм (б)
Результаты (рисунок 1 и рисунок 2) характеризуют одиночную дисперсную частицу.
При прохождении излучения с длиной волны через слой толщиной l, содержащий равномерно распределенные частицы диаметром d с концентрацией Cm, спектральный коэффициент ослабления в соответствии с законом Бугера определяется следующим образом:
где T – спектральный коэффициент пропускания, вычисляемый по формуле:
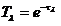
,
Оптическая толща слоя выражается через концентрацию Cm, толщину слоя l и спектральный коэффициент ослабления k одиночной частицы (1) следующей зависимостью [3]:
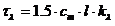
,
Аналогично определяются спектральные коэффициенты рассеяния и поглощения слоя.
Индикатриса рассеяния рассчитывается по формуле
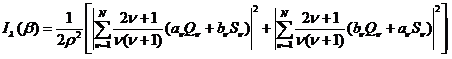
,
где av и bv – коэффициенты Ми, Qv и Sv – угловые функции, в – угол рассеяния.
Угловые функции Qv и Sv рассчитываются с помощью полиномов Лежандра, где µ=cos(в), и их производных:
На рисунке 3 представлены индикатрисы рассеяния излучения кавитационными пузырями различного диаметра.
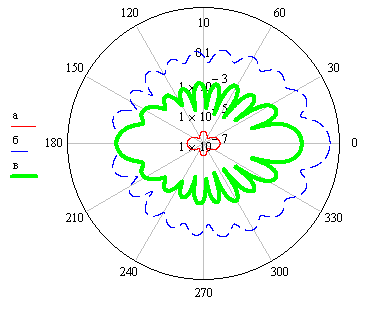
Рисунок 3 – Зависимость индикатрисы рассеяния от размера частицы для длины волны 0,5 мкм и d1=0,01 мкм (а), d2=2 мкм (б), d3=8 мкм (в)
Из рисунка 3 видно, что при диаметре частиц, соизмеримом с длиной волны излучения, индикатриса может иметь достаточно сложную форму, что необходимо учитывать при проведении экспериментальных исследований.
Результаты исследований позволяют:
-прогнозировать величины спектральных коэффициентов поглощения, рассеяния и ослабления кавитационной области по известным оптическим характеристикам материалов среды, частиц, диаметру частиц и их концентрации;
–прогнозировать вид индикатрисы рассеяния кавитационной области для известных длин волн излучения и диаметров частиц;
–выбирать спектральный диапазон и подходящий метод экспериментального исследования кавитационной области.
Список использованной литературы
1. Дейрменджан Д. Рассеяние электромагнитного излучения сферическими полидисперсными частицами / Под ред. Д. Дейрменджана. – М.: Мир, 1971. – 168 с.
2. Галенко Ю.А., Сысоева М.О. Моделирование коэффициента теплового излучения полубесконечной дисперсной среды // Ползуновский вестник. - Барнаул: АлтГТУ - 2008. ? № 1-2. ? С. 28-32.
3. Архипов В.А. Лазерные методы диагностики гетерогенных потоков /В.А. Архипов. – Томск: Изд-во Томского университета, 1987. – 140 с.
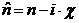 , где x - главный показатель поглощения материала, n - показатель преломления.
, где x - главный показатель поглощения материала, n - показатель преломления.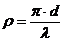
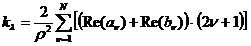 (1)
(1)
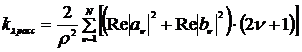
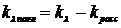


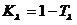
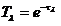 ,
,
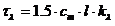 ,
,
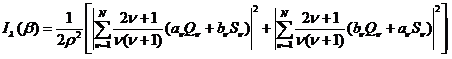 ,
,