Быстродействующий алгоритм определения поврежденной фазы сети с изолированной нейтралью
Авторы: Чорноус Е.В., Готин Б.А, Чорноус В.П.
Источник: Донецкий национальний технический университет
Analytical research of weight integral indexes of man's defeat was conducted. This man was under phase tension of mine district network with the use of the shunting assisted. The algorithm of identification defective phase was offered. Also the capacity of algorithm was explored at the influence of factors that were bringing errors in his work.
Одним из вариантов защиты человека от поражения электрическим током является защитное шунтирование. Его сущность заключается в искусственном автоматическом соединении с землей поврежденной фазы (фазы, в которой выявлена утечка тока на землю). Наиболее ответственным звеном защитного шунтирования является устройство выбора (идентификации) поврежденной фазы (УВФ) [1]. Требования к УВФ противоречивы. С одной стороны необходимо максимальное быстродействие (человек под напряжением). С другой стороны, случайное шунтирование неповрежденной, “здоровой“ фазы до срабатывания защитного отключения недопустимо.
В [2] описан быстродействующий способ определения поврежденной фазы, сущность которого заключается в определении аргумента (начальной фазы) потенциала нейтрали по двум смежным точкам его мгновенного значения u(t) и u(t+ Δt). Если разница по фазе между этими точками Δωt фиксирована и находится в пределах от 10 до 20 градусов, задача сводится к решению системы:

При возникновении утечки УВФ и алгоритм, реализующий предложенный способ, находятся под интенсивным воздействием помех и искажений со стороны сети, находящейся в переходном режиме. Кроме того, нельзя исключить влияние высших гармоник, находящихся в составе потенциала нейтрали. В этих условиях надежность идентификации обеспечивается тем, что решение принимается не по одному значению аргумента φ, а по серии промежуточных результатов, содержащей от 5 до 15 значений в зависимости от интенсивности помех и искажений со стороны сети. Совместная обработка этих результатов, их усреднение и анализ итогового результата позволяют безошибочно определить (идентифицировать) аварийную фазу. Однако требование максимального быстродействия приводит к необходимости минимизации времени, отводимому для многократного определения значений аргумента φ.
Цель данной работы – повысить быстродействие УВФ путем замены итерационных методов решения системы (1, 2) на алгоритм ее аналитического решения. Достигается это следующим. Исключая из системы (1 и 2) амплитуду Uмах, получаем:

и далее

Составляющие выражения (4) можно представить (изобразить) векторами, вращающимися на комплексной плоскости, т.е. комплексными функциями времени или просто комплексами:

В то время, как комплекс В является единичным, комплекс А опережает его на постоянный угол Δωt и имеет переменную амплитуду (модуль). Однако главной особенностью этих комплексов является, как следует из (4), равенство их мнимых составляющих. Это значит, что их разность С содержит только действительную составляющую

Геометрическая интерпретация комплексов (5), (6) и (7) приведена на рис.1, где отрезками а, в, с, образующими замкнутый треугольник, обозначены модули комплексов А, В, С соответственно.
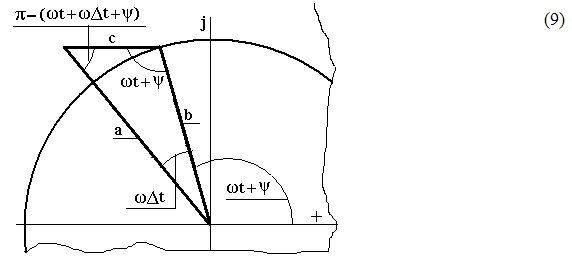
Рисунок 1 – Геометрическая интерпретация комплексов.
Причем, характерной особенностью этого треугольника является то, что, как следует из выражения (4), отрезок с параллелен действительной оси и, кроме того, его углы выражаются через величины, входящие в выражения (1)…(4). Используя эти особенности треугольника, отрезок с можно определить непосредственно из теоремы косинусов:

Далее, используя для этого же треугольника известное выражение (теорема синусов), получим:
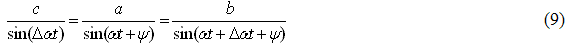
Полученное выражение (9) позволяет вычислить аргумент φ потенциала нейтрали. Однако этот результат нуждается в проверке из-за возможности появления лишних
корней. Простейшей формой проверки следует считать вычисление амплитуды потенциала нейтрали Umax из выражения (1) или (2) подстановкой проверяемого значения φ. Если амплитуда положительна, корень подходит, в противном случае к проверяемому значению φ добавляется (или вычитается) половина периода.
Следует отметить, что определение амплитуды Umax кроме промежуточной проверки и отбрасывания лишних
корней несет добавочную информационную нагрузку, позволяющую косвенно определить величину сопротивления утечки необходимую для принятия взвешенного решения.
В качестве системы отсчета в данном исследовании по умолчанию
принимается момент перехода через нуль линейного напряжения Uab при его возрастании.
Из всего изложенного следует следующий упрощенный алгоритм определения аргумента (начальной фазы) потенциала нейтрали относительно принятого начала отсчета.
- Производится слежение за средним по модулю значением потенциала нейтрали |φ0 | и если эта величина превысит допустимое значение, запускается в работу программа определения промежуточных значений аргумента φ.
- Для моментов времени t и t+ Δt фиксируются мгновенные значения потенциала нейтрали u(t) и u(t+ Δt) и определяется А = u(t)/u(t+Δt).
- Осуществляется проверка условия 0.1 < |А| < 10.0 , (10) при невыполнении которого следует вернуться к п. 2. (Этот пункт обусловлен необходимостью избежать недопустимого возрастания относительной погрешности отношения u(t)/u(t+Δt), если какое либо из его значений окажется вблизи нуля).
- Из выражений (8) и (9) определяется очередное промежуточное значение φ.
- Полученное значение φ проверяется на одном из выражений (1) или (2) путем вычисления амплитуды Umax, причем, если Umax < 0, то φ = φ + π.
- Промежуточные значения аргумента φ и амплитуды потенциала нейтрали Umax усредняются, после чего принимается решение или на применение защитного шунтирования, или на продолжение вычислений промежуточных значений.
ЛИТЕРАТУРА
- Чорноус Е.В., Ковалев А.П., Чорноус В.П. Об оценке электробезопасности сети с изолированной нейтралью // Электричество. 2006. №5. C.
- Шуцкий В.И., Жидков В.О., Ильин Ю.Н. Защитное шунтирование однофазных повреждений электроустановок. – М.: Энергоатомиздат, 1986. – 152 с.:ил.
- Дзюбан В.С. Аппараты защиты от токов утечки в шахтных электрических сетях М., Недра, 1982. 152 с.
- ГОСТ 12.1.038 – 82. Электробезопасность. Предельно допустимые уровни напряжений прикосновения и токов. Издательство стандартов, 1983.