Анализ методики идентификации параметров двигателей постоянного тока в рамках системы стабилизации конструкции в виде перевернутого маятника

Аннотация

Градзявичус В. В., Суков С. Ф. - Анализ методики идентификации параметров двигателей постоянного тока в рамках системы стабилизации конструкции в виде перевернутого маятника. Рассмотрена методика идентификации модели двигателя постоянного тока независимого возбуждения.

Рассмотрим методику идентификации параметров двигателя постоянного тока. В результате должна быть получена передаточная функция двигателя, которая в дальнейшем будет учтена в синтезе закона управления.

Двигатель постоянного тока (ДПТ) независимого возбуждения описывается следующей системой уравнений:

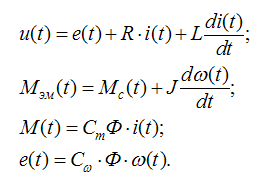
(1)

Где u(t) – напряжение на якорной обмотке двигателя; e(t) – э.д.с. якоря; i(t) – ток якоря; Ф – поток, который создается обмоткой возбуждения; М_эм(t) – электромагнитный момент двигателя; М_c(t) – момент сопротивления движения; w(t) – скорость вращения вала двигателя; R – активное сопротивление якорной цепи; L – индуктивное сопротивление якорной цепи; J – суммарный момент инерции якоря и нагрузки; C_w – электромагнитная постоянная двигателя; C_m – механическая постоянная двигателя.

Для создания модели двигателя необходимо получить передаточные функции, применив к дифференциальным уравнениям преобразования Лапласа. Передаточная функция, которая характеризует ток якоря и падения напряжения на якоре:

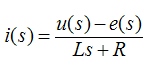
(2)

Передаточная функция, которая связывает динамический момент и скорость вращения вала двигателя:

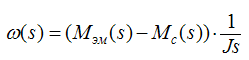
(3)

Используя полученные передаточные функции можно получить переходные процессы двигателя по току и скорости. Однако, бывают случаи когда параметры двигателя неизвестны, имеется возможность лишь снять кривую разгона, например, по скорости.

Предположив, что кривая разгона была получена экспериментально, т.е. были обработаны показания встроенного в двигатель энкодера, проведем идентификацию динамических характеристик двигателя методом Симою[1]. Данный метод является одним из наиболее удобных при использовании ЭВМ для идентификации объекта управления в условиях проведения активного эксперимента. Предполагается, что объект может быть описан линейным дифференциальным уравнением с постоянными коэффициентами:

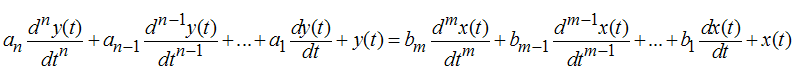
(4)

где 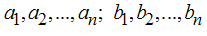- постоянные коэффициенты.

Задача состоит в том, чтобы определить неизвестные коэффициенты a_i и b_i используя специальную систему уравнений:

(5)

Параметры F_i , входящие в эту систему уравнений имеют аналитические выражения:

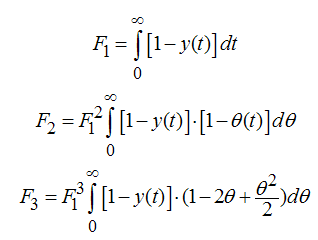
(6)

где - измененный масштаб по времени

Для вычисления коэффициентов F_i необходимо придерживаться определенной последовательности расчета:

1. Ось абсцисс разбивается на отрезки с интервалами времени , исходя из условия, что на протяжении всего графика, y_вых(t) в пределах 2 мало отличается от прямой.

2. Значения вектора y_вых(t) в конце каждого интервала делятся на . В результате получается вектор

3. Определяются коэффициенты F₁, F₂, F₃ по формулам:

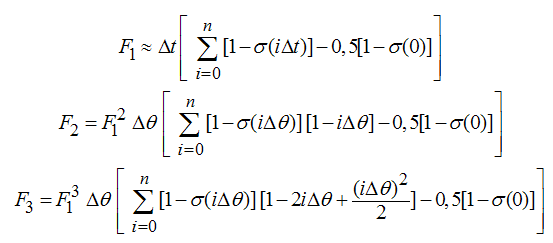
(7)

Для оценки погрешности рассчитывается среднеквадратическое отклонение:

(8)

где 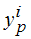- i-тый расчетный элемент выборки; 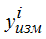- i-тый измеренный элемент выборки;

Проанализировав кривую разгона по скорости, как правило замечают, что данная кривая напоминает типовую кривую разгона апериодического звена 2-го порядка с передаточной функцией:

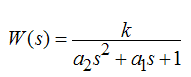
(9)

Следуя вышеприведенному алгоритму рассчитываются коэффициенты F_i и по ним определяются коэффициенты a_i. В результате получают передаточную функцию модели.

Выводы:

Метод площадей Симою является одним из самых простейших алгоритмов определения параметров передаточных функций моделей объектов по кривой разгона. Однако в силу своей простоты, данная методика довольно часто может давать неудовлетворительные результаты – идентифицированные параметры моделей объектов могут иметь большое отклонение в сравнении с реальными динамическими характеристиками. В связи с этим возникает необходимость в поисках и синтезе альтернативных методик идентификации параметров ДПТ.

Список использованной литературы

1. Симою М.П. Определение коэффициентов передаточных функций линеаризованных звеньев систем регулирования. Автоматика и телемеханика, 1957г., №6. С. 514-527
2. Льюнг Л. Идентификация систем. Теория для пользователя: М.: Наука, 1991г., 432 с.
3. Ерофеев А.А. Теория автоматического управления: Учебник для вузов. – 2-е изд., перераб. и доп. – СПб.: Политехника, 2001. – 302 с.: ил. С. 34
4. Эйкхофф П. Основы идентификации систем управления. Оценивание параметров и состояния.–М.: Мир, 1975г., 687 с.