Назад в библиотеку

Идентификация и моделирование перевернутого маятника PS600

Автор: Jiri Marholt, Frantisek Gazdos
Перевод: Градзявичус В.В.
Источник: Сборник Montanistica Slovaca, Том 15 (2010) №1, 14-18

Аннотация

Jiri Marholt, Frantisek Gazdos - Идентификация и моделирование перевернутого маятника PS600. Данная работа посвящена получению модели, идентификации и моделированию перевернутого маятника PS600. Эта система является неустойчивой и нелинейной с одним входом – напряжение двигателя постоянного тока, который может изменить положение тележки и два выхода – положение тележки и угол наклона стержня маятника. Сначала, выводится математическая модель перевернутого маятника с последующей идентификацией его неизвестных параметров. Затем модель реализуется в среде MATLAB Simulink и ее свойства экспериментально сравниваются со свойствами реальной системы.

Введение

В промышленности существует множество процессов и объектов, которые обладают нестабильным поведением, например, различные типы реакторов, системы сгорания, дистилляционные колонны и т.д. В режиме реального времени эксперименты с этими системами без надлежащего контроля могут представлять реальную опасность. В таких случаях процесс моделирования часто является единственным надежным инструментом для исследования свойств таких систем. В настоящее время, роль моделирования выросла в основном благодаря увеличению производительности компьютерных технологий. Есть много других источников, посвященных этим областям науки.

Этот материал ориентирован на получение математической модели и дальнейшего моделирования системы перевернутого маятника PS600, который представляет собой один тип неустойчивых систем. Данная система является продуктом компании AMIRA и может быть найден в лабораториях департамента управления технологическими процессами, факультет прикладной информатики Томаша Бати, университет в городе Злин. Целью данной работы является разработка надежной математической модели системы вместе с ее линеаризованной версией и соответствующей средой для моделирования, что поможет как студентам, так и исследователям экспериментировать с этой неустойчивой системой. Полученная модель затем реализована в среде MATLAB / Simulink.

Работа построена следующим образом: после введения, следует описание системы вместе с предложенной математической моделью и ее параметрами. Далее, выполняется линеаризация в выбранных рабочих точках и, как следствие, анализируются передаточные функции. Затем, выполняется сравнение предлагаемой математической модели с реальной системой и делаются некоторые выводы.

Перевернутый маятник

Система состоит из тележки, которую можно перемещать вдоль металлической направляющей планки. Алюминиевый стержень с цилиндрический грузом прикреплен с тележке по оси. Эта система является неустойчивой и нелинейной с одним входом и двумя выходами. Входным сигналом является управляющее напряжение электродвигателя постоянного тока, который может изменить положение тележки. Выходами являются положение тележки и угол отклонения стержня маятника. Оба выхода измеряется инкрементальными энкодерами. Схема системы представлена на рисунке 1.

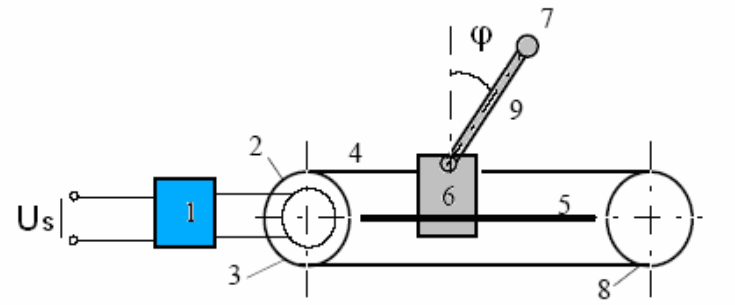
Рисунок 1. - Схема системы перевернутого маятника

где 1 — серво-усилитель, 2 — двигатель постоянного тока, 3 — привод, 4 — ремень привода, 5 — металическая направляющая планка, 6 — тележка, 7 — груз маятника, 8 — направляющий ролик, 9 — стержень маятника.

Математическая модель

Система может быть описана следующими нелинейными дифференциальными уравнениями:

(1)

(2)

где F представляет входной сигнал, который является силой производимой двигателем постоянного тока. Выходными сигналами являются r — позиция тележки, r' — скорость тележки, 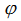— угол отклонения маятника от нормали к поверхности, — угловая скорость маятника. Символ g представляет ускорения свободного падения, а F_r — является константой вращательной скорости пропорциональной трению тележки. Все константы и обозначения определены в таблице 1. Следующие замены были произведены в уравнениях (1) и (2):

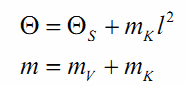
(3)

(4)

где m_v — масса тележки, m_k — масса маятника, l — расстояние между центром масс маятника и центром точки вращения маятника, — момент инерции стержня маятника, относительно центра масс.

Таблица 1

Параметер	Обозначение	Значение и единица измерения
Масса тележки	m_v	4 кг
Масса маятника	m_k	0,42 кг
Общая масса	m	4,42 кг
Длиня стержня маятника	l	0,42 м
Момент инерции		0,08433 кг*м²
Скорость вращения пропроциональная трению тележки	F_r	6,5 Н
Трение тежелки	F_c	15 Н
Трения маятника	C	0,0006 кгм²s^-1
Константа скорости реакции	k_A	7,5

Линеаризация

С целью упрощения проектирования системы управления, нелинейный дифференциальные уравнения (1) и (2) описывающие поведение перевернутого маятника были линеаризованы в рабочих точках 0 (нижняя позиция маятника) и π (верхняя позиция маятника). В итоге были получены следующие нижеприведенные передаточные функции.

Передаточная функция позиции тележки для рабочей точки 0 выглядит так:

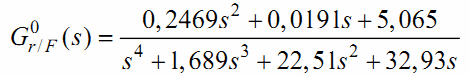
Анализируя полюса и нули передаточной функции, можно определить, что система является устойчивой, периодической

Передаточная функция угла отклонения маятника для рабочей точки 0 имеет вид:

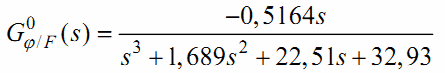
Проанализировав полюса и нули данной передаточной функции, также можно утвеждать, что система устойчива.

Передаточная функция позиции тележки для рабочей точки π:

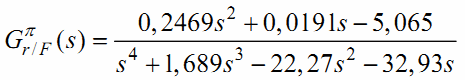
Анализ поюсов и нулей показал, что данная система является колебательной неустойчивой.

Передаточная функция угла отклонения маятника для рабочей точки π имеет вид:

Данная система, как и предыдущая также является неустойчивой.

Моделирование

С помощью среды MATLAB, в частности приложения Simulink и интрумента Real-Time (Humusoft, 2003), было исследовано поведение перевернутого маятника для выбранных значений управляющего сигнала. Затем полученные данные положения тележки и угол поворота маятника были сравнены со данными, полученными в результате моделирования с использованием предлагаемой математической модели.

В следующих экспериментах, был использован управляющий сигнал со значением -0,3, который воздействовал на систему около 4-5с. Нижеприведенные графики на рисунках 2 и 3 показаны кривые математической и реальной моделей. Пояснения по обозначениям: rs - управляющее воздействие, p_n - позиция тележки в реальной системе, p_s - позиция тележки в математической моделе, uⁿ - угол отклонения маятника в реальной системе, u^s - угол отклонения маятника в математической модели.

Рисунок 2 - Позиция тележки для математической и реальной систем

Рисунок 3 - Угол отклонения маятника от нормали к поверхности для математической и реальной систем

Дальнейшее сравнение было выполнено с использование ПИ-регулятора при управлении позицией тележки, где был примен классический метод Гурвица для проверки устойчивости замкнутых систем. Результирующая реакция на управляющее воздействие представлена на рисунке 4.

Рисунок 4 - Управление позицией тележки с использованием ПИ-регулятора

В результате сравнительного анализа можно сделать вывод, что предложенная математическая модель описывает поведение системы в реальном времени достаточно точно, по крайней мере с точки зрения управляемой переменной.

Выводы:

Целью данной работы было получение математической модели, идентификация и моделирование перевернутого маятника PS600. Реальный прототип находится в лаборатории департамента управления технологическими процессами, факультет прикладной информатики, университет Томаша Бати в городе Злин. Итоговые нелинейные дифференциальные уравнения описывающие поведение системы были реализованы в среде MATLAB / Simulink с помощью специального блока "S-Function". Свойства предлагаемой математической модели были сопоставлены с ее реальным аналогом. Результирующая кривые позиции тележки и угловое смещение перевернутого маятника для выбранных значений управляющего сигнала показаны на рис. 2-3.

Затем сравнение моделей было проведено во время управления положением тележки с помощью ПИ-регулятора см. рис. 4. Из приведенных графиков можно сделать вывод, что динамика предлагаемой математической модели соответствует реальной системе достаточно хорошо. В результате, предложенная модель может быть дополнительно использована как для анализ и синтеза этой системы. Кроме того, полученные передаточные функции перевернутой маятника в различных рабочих точках могут быть использованы для дальнейшей оптимизации и экспериментов с этим типом неустойчивых систем.

Список использованной литературы

1. Amira: PS600 Laboratory Experiment Inverted Pendulum. Duisburg : Amira GmbH, 2000, 351 pp.
2. Chalupa, P., Bobál, V.: Modelling and predictive control of inverted pendulum. In 22nd European Conf. Modelling and Simulation. Nicosia, Cyprus : Digitaldruck Pirrot GmbH Sbr.-Dudweiler, 2008, pp. 531-537. ISBN 978-0-9553018-5-8.
3. Dabney, J. B., Harman, T. L.: Mastering Simulink. Prentice Hall, 2004. ISBN 0-13-142477-7.
4. Dostál, P., Gazdoš, F.: Control of technological processes Zlín : Tomas Bata University in Zlín, 2006. 98 pp. ISBN 80-7318-465-6.
5. Hanselman, D. C., Littlefield, B.: Mastering Matlab 7. Prentice Hall, 2005. ISBN 0-13-143018-1.
6. Humusoft: Real time toolbox - user’s manual. Prague : Humusoft s.r.o., 2003.
7.Marholt, J.: Modelling, identification and simulation of the inverted pendulum PS600 (in Czech). Diploma thesis. Zlín : Tomas Bata Univ. in Zlín, 2008, 75 pp.
8. Severance, F. L.: System modeling and simulation. Chichester : Wiley, 2001, 518 pp., ISBN 0471496944.
9. Stein, G.: Respect the unstable. IEEE Control system Magazine. August 2003, pp. 12-25., 2003.