Анализ и оценкас существующих методов стабилизации конструкции в виде перевернутого маятника

Аннотация

Баранов Б. М., Суков С. Ф. Анализ и оценка существующих методов стабилизации конструкции в виде перевернутого маятника. В данной работе рассмотрены основные алгоритмы, используемые для стабилизации конструкции в виде перевернутого маятника, приведены сравнительные графики переходных процессов, а также указаны достоинства и недостатки регуляторов.

Системы стабилизации и динамического равновесия становятся в наше время все более сложными и распространенными не только на производстве, а также и в повседневной жизни. Этому также способствует быстрое возрастание вычислительных мощностей микроконтроллеров, способных с большой частотой контролировать положение системы, развитие микромеханических систем, а именно датчиков перемещения (положения). В наше время размеры этих датчиков постепенно уменьшаются, а точность и чувствительность постепенно возрастают.

Одной из самых распространенных систем динамического равновесия является система робота в виде перевернутого маятника. Она уже получила широкое распространение в системах автоматизации и робототехнике благодаря своей простоте и высокой маневренности. Использование для таких систем современных микромеханических датчиков перемещения позволяет осуществлять все большую миниатюризацию и доступность таких систем, что, в свою очередь, позволяет расширять область их использования.

Конструкции в виде перевернутого маятника имеют следующий вид: на единой колесной оси находится груз, центр тяжести которого находится значительно выше колесной оси.

В чем же заключается идея балансирования? Конструкция имеет одно положение равновесия – параллельное нормали к земной поверхности. Для равновесия необходимо, чтобы сумма внешних сил, приложенных к телу, была равна нулю, а также, чтобы сумма моментов всех сил, приложенных к телу относительно любой оси, была равна нулю. Таким образом, центр масс такого тела должен оставаться в покое. Если он перемещается в сторону, то сила земного притяжения придает конструкции вращающий момент, который способствует заваливанию конструкции. Для обеспечения положения равновесия необходим вращательный момент, направленный к положению равновесия. Таким образом, чтобы скомпенсировать силу земного притяжения, система должна осуществлять движение с ускорением в сторону падения [1, c. 184].

Из рассуждений выше следует, что процесс поддержания равновесия такой системы можно разделить на две составляющие:

1) определение угла наклона конструкции от положения равновесия;

2) управление вращением колес в зависимости от величины отклонения для формирования момента, который компенсирует падение.

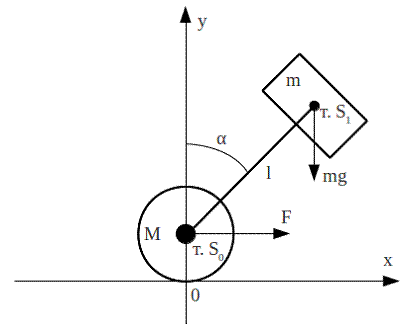
Рассмотрим конструкцию, изображенную на рисунке 1. М – масса колесной базы такой конструкции,  m – масса груза, α – угол отклонения маятника от нормали к земной поверхности, т. S₀ – центр масс колесной базы, т. S₁ – центр масс груза, l – расстояние между т. S₀  и т. S₁, g – ускорение свободного падения, r – радиус колеса.

Для получения математического описания исследуемого объекта воспользуемся вторым законом Ньютона и методом виртуальной работы:

 

.

 

Перемещение т. S₀:

 

.

.

Рисунок 1 – Физическая модель объекта.

 

Ускорение т. S₀:

 

.

 

Перемещение т. S₁:

 

.

 

Перемещение т. S₁:

 

.

 

Исходя из цели управления (минимальное отклонение маятника от вертикальной оси, при котором ) выполнив упрощение , , получим:

 

, .

 

С учетом выполненного упрощения по второму закону Ньютона получаем систему уравнений второго порядка, описывающую исследуемый объект:

 

 

Полученная система уравнений позволяет рассчитать законы управления объектом, самые распространенные и эффективные из которых рассмотрены в данной статье.

Классическим алгоритмом балансирования, хорошо зарекомендовавшим себя в задачах управления неустойчивыми объектами, считается ПИД-алгоритм. ПИД-регулятор прост в реализации и настройке. Проектирование регуляторов данного типа является широко распространенной задачей, существует множество методик расчета коэффициентов его составляющих. Однако, программная реализация ПИД-алгоритма может быть связана с определенными трудностями, особенно при ограниченных вычислительных возможностях  микропроцессорных устройств. Кроме того, ПИД-алгоритм довольно чувствителен к изменению коэффициентов усиления. Как показывает практика, изменение одного из оптимального набора коэффициентов на 10% может привести к потере устойчивости системы стабилизации маятника.

Для наглядности, продемонстрируем результаты работы ПИД-регулятора для объекта в виде перевернутого маятника, осуществленную в программном комплексе MATLAB при помощи пакета Simulink и блока PID-Controller. Настройка коэффициентов регулятора выполнена с помощью программного средства PID-Tune блока PID-Controller:

 

 

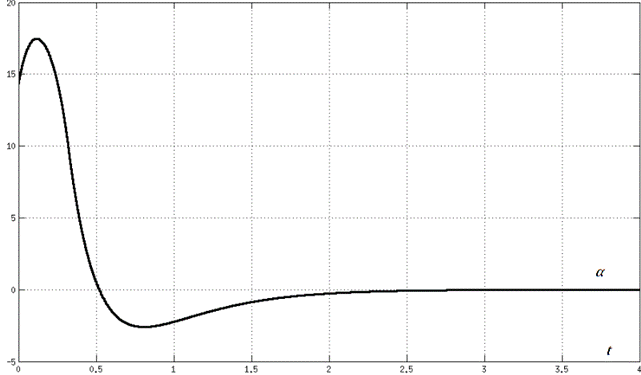
Рисунок 2 – Результаты стабилизации системы с ПИД-регулятором

 

Как видно из графика представленного на рисунке 2, при начальных условиях угла наклона маятника в 15 градусов, ПИД-регулятор показывает хорошее быстродействие и малое перерегулирование, восстанавливая положение равновесия конструкции приблизительно за 2 секунды.

Однако, несмотря на хорошие показатели использования ПИД-регулирования для задачи стабилизации, специалисты в области автоматики ищут альтернативные алгоритмы управления объектами, выполненными в виде перевернутого маятника. Причиной этого служит тот факт, что, учитывая несовершенство систем определения угла наклона, сигнал обратной связи в контуре управления углом наклона подвержен различным возмущающим воздействиям, связанным с физическим устройством микромеханических датчиков. Кроме того, сложность обработки показателей таких датчиков требует значительных производительных мощностей от микропроцессорных устройств. Таким образом, практическая реализация ПИД-регулирования на реальном объекте сталкивается с рядом проблем, вынуждающих обратиться к иным алгоритмам управления.

Одним из самых распространенных типов регуляторов в последние годы становятся модальные регуляторы. Синтез регуляторов модального управления базируется на корневых методах, качество переходных процессов в системах модального регулирования определяется размещением корней характеристического полинома системы на комплексной плоскости, поэтому модальные регуляторы удобно использовать для объектов, которые позволяют измерить каждую переменную состояния системы в пространстве состояний.

Как правило, в исследуемых системах для определения угла наклона конструкции используются МЕМС-датчики двух типов – акселерометр и гироскоп, обработка данных которых с помощью фильтрации позволяет добиться лучших результатов. На основании того, что акселерометр позволяет измерять угол наклона в статическом режиме (при неподвижной конструкции), а гироскоп – скорость его изменения, возникают определенные причины, указывающие на перспективность исследования возможности использования модального регулятора в контуре балансировки конструкции.

Уравнение системы в пространстве состояний (для контура регулирования угла наклона):

 

,

.

 

Для нахождения коэффициентов модального регулятора воспользуемся размещением корней, соответствующим размещения корней полинома Баттерворта соответствующего порядка:

 

,

 

где  – собственная частота системы. Подобрав оптимальную собственную частоту, получаем следующий график переходного процесса:

 

Рисунок 3 – Переходный процесс в системе с модальным регулятором

 

Однако, хотя модальный регулятор показывает качественные результаты в контуре балансирования и достаточно легок в реализации, на данный момент использование его в исследуемой системе также затруднительно. На показания акселерометра, который измеряет переменную состояния угла наклона, действует также ускорение конструкции вдоль его линии его перемещения, которое задается управляющим воздействием. Даже в случае возможности точного измерения ускорения конструкции вдоль линии перемещения (например, с помощью обработки показаний дополнительных датчиков перемещения – энкодеров и т.п.), его не возможно выделить из показаний двухосевого акселерометра. И все же дальнейшие исследования в сфере использования модального управления для объектов исследуемого типа, поиск альтернативных технических средств измерения могут сделать использование модального регулирования в задаче балансировки возможным.

Еще одним перспективным видом регуляторов являются регуляторы, основанные на применении нечеткой логики. Нечеткое регулирование позволяет во многом решить самые главные проблемы в задаче балансировки объекта в виде перевернутого маятника, а именно сложность идентификации объекта и неточность показаний измерений объекта в динамическом режиме. Нечеткое регулирование представляет собой несколько этапов: фаззификация (конвертация входной переменной из четкого значения в нечеткую лингвистическую переменную), активация (активация нечетких правил), преобразование (применение нечетких правил), аккумуляция (формирование нечеткого вывода) и дефаззификация (формирование управляющего воздействия) [2, c. 29].

Произведем реализацию системы нечеткого управления, пользуясь встроенными средствами соответствующего блока функций из пакета Simulink программного комплекса MATLAB. Для каждого входа модуля нечеткого управления (угол и угловая скорость) зададим четыре функции принадлежности. С использованием алгоритма накопления знаний, в ходе обработки обучающей последовательности – 90 пар данных, полученных при наблюдении функционирования ПИД-регулятора, сформированы 16 нечетких правил. Для реализации нейронной сети, выполняющей дефаззификацию, воспользуемся трехслойной сетью со структурой 5+2+1 с сигмоидальной функцией активации. В результате тестирования спроектированного модуля управления получен следующий график:

Рисунок 4 – Переходный процесс в системе с нечетким регулятором

 

Насколько видно из графика, нечеткий регулятор обеспечивает большее перерегулирование, чем рассмотренные прежде алгоритмы регулирования угла наклона конструкции в виде перевернутого маятника, но при этом достаточно короткий переходный процесс. Варьирование параметров нечеткого регулятора, несомненно, может привести к лучшему результату. Данный алгоритм регулирования на текущий момент активно распространяется и приобретает популярность, как надежный и робастный закон.

 

Список использованной литературы

1. Мякишев Г. Я. Физика. Механика / Мякишев Г. Я. – М.: Дрофа, 2004. – 385 с.

2. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польск. И. Д. Рудинского. – М.: Горячая линия –Телеком, 2006. – 452 c.