Назад в библиотеку
Идентификация параметров подводного робота в среде MatLab
Аннотация
Герасимова Ю.В. - Идентификация параметров подводного робота в среде MatLab. Предлагается решение задачи параметрической идентификации на примере идентификации массы подводного робота. Рассматривается вопрос о выборе исполнительного механизма стабилизатора глубины подводного робототехнического комплекса
Проблема оптимизации управления подводными роботами (ПР) непосредственно связана с проблемой параметрической идентификацией. Это объясняется нестационарностью и широким диапазоном изменения гидродинамических параметров ПР в процессе управления [1].
Целесообразно для идентификации гидродинамических параметров ПР использовать пакет Simulink системы Matlab [2].
Предлагается следующее решение задачи параметрической идентификации на примере идентификации массы подводного робота M, с учетом присоединенных масс и гидродинамического сопротивления c, которая в общем случае сводится к определению постоянных времени T1=М и T2=с в уравнении (1):
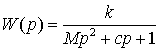
(1)
Идентификация осуществляется с помощью подстраиваемой модели и алгоритма идентификации, основанного на способе поиска экстремума с помощью метода градиента [3]. Общая форма организации движения к экстремуму по градиентным методам сводится к такому изменению вектора варьируемых параметров A, при котором его скорость изменения связана с градиентом J соотношением:
 (2)
(2)где J(ε) – минимизируемый функционал ошибки ε, B = [k1 k2] – некоторая квадратная матрица, A = [T1 T2]T, gradJ(ε) = [∂J/∂T1 ∂J/∂T2]T. При использовании достаточно простого функционала в виде половины квадрата ошибки J = ε2(t)/2 компоненты градиента определяются по обычному правилу дифференцирования сложной функции:

(3)
На рис. 1 представлена Simulink-модель системы идентификации параметров ПР.
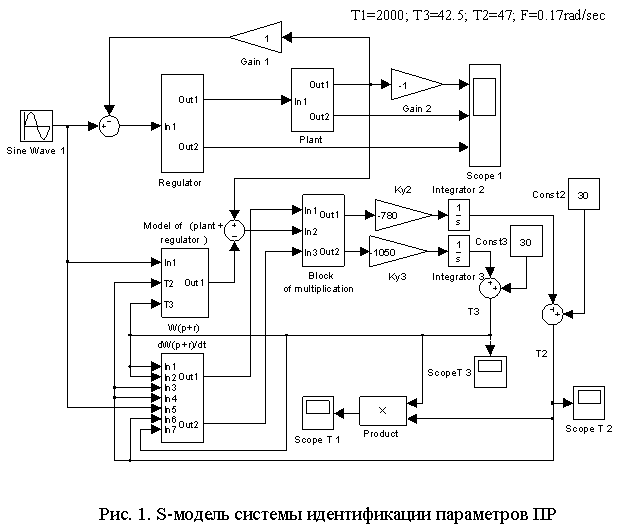
На рис. 5 и 6 представлены результаты идентификации постоянных времени T1 = 2000 и T2 = 47.

Визуальный анализ результатов моделирования свидетельствует о достаточно хорошей точности идентификации гидродинамических параметров ПР как объекта управления.
Одной из важных задач систем управления малогабаритными подводными самоходными аппаратами, предназначенными для выполнения подводных работ, т.е. выполняющих функции роботов, является стабилизация подводных аппаратов на заданной глубине. При этом к основным требованиям, предъявляемым к подобным системам, помимо точности относится требование минимального потребления электроэнергии [1]. Успешное решение задачи минимизации потребления энергии стабилизаторами глубины (СГ) зависит от того насколько точно определены динамические параметры подводного робототехнического комплекса (ПРК) как объекта управления. К таким параметрам можно отнести массу ПРК и коэффициент динамического сопротивления воды. Масса ПРК включает присоединенную массу воды, которая зависит как от формы подводного аппарата, так и от скорости его движения. От скорости движения зависит и сила гидродинамического сопротивления. Также изменение массы ПРК может определяться и функциональным назначением робототехнического комплекса.
Наиболее эффективным методом определения динамических характеристик ПРК является метод параметрической идентификации. В данном случае отдадим предпочтение беспоисковому компенсационному методу известному под названием "метод вспомогательного оператора" [2], где используются самонастраивающаяся модель с настройкой параметров по градиенту функционала рассогласования выходов объекта и модели объекта при общем входном сигнале и вспомогательные операторы для получения частных производных по настраиваемым параметрам от сигнала рассогласования выходов объекта и модели.
Наиболее важной составляющей в этой технологии является точность измерения входного и выходного сигналов. Выходной сигнал (информация о глубине нахождения ПРК) измеряется с высокой точностью датчиком давления. Вход объекта и модели принадлежит одновременно и выходу исполнительного механизма. Поэтому выбор исполнительного механизма управляющего глубиной погружения ПРК необходимо проводить не только по критерию точности управления, но и с учетом возможности измерения выходного сигнала. Обоим этим требованиям удовлетворяет поршневой вытеснитель (ПВ) балластной воды, управляемый электродвигателем постоянного тока. Во-первых, в этом случае обеспечивается возможность точного регулирования остаточной плавучести ПРК, во-вторых, с помощью потенциометра, соединенного с поршнем вытеснителя можно точно измерять объем принятой и вытесненной воды, т.е. измерять выходной сигнал ПВ. На рис. 1 представлена структура системы управления ПРК.
На рисунке приняты следующие обозначения: БК – бортовой компьютер (формирует алгоритм управления); ТП – трехпозиционный бесконтактный
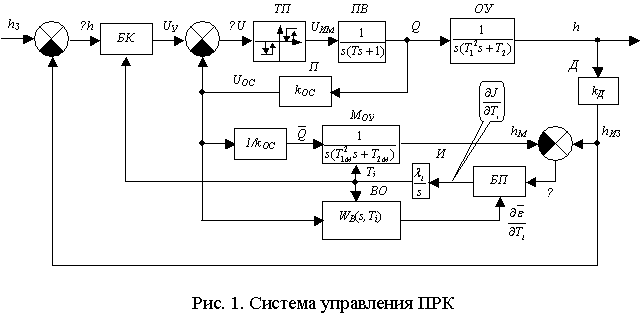
переключатель (усилитель); ПВ – исполнительный механизм, включающий электродвигатель и поршневой вытеснитель; П – потенциометр; ОУ – объект управления; Д – датчик давления; МОУ – модель объекта управления; ВО – вспомогательный оператор; БП – блок перемножения; И – интегратор; T1 – постоянная времени, характеризующая массу ОУ; T2 – постоянная времени, характеризующая гидродинамическое сопротивление; hЗ, h – заданная и измеренная глубины нахождения ОУ соответственно; ε – сигнал рассогласования (ошибка) между выходами ОУ (hМ) и модели МОУ (hИЗ); Q – плавучесть ОУ; J = ε 2(t) – функционал ошибки ε,  – компоненты градиента функционала; T = {T1,T2} – вектор параметров; λi – diag {λ1, λ2} – вектор коэффициента усиления в контуре самонастройке.
– компоненты градиента функционала; T = {T1,T2} – вектор параметров; λi – diag {λ1, λ2} – вектор коэффициента усиления в контуре самонастройке.
Контур, включающий элементы ТП, ПВ и П, представляет собой широтно-импульсный модулятор, который обеспечивает энергосберегающий режим работы исполнительного механизма и в тоже время позволяет измерять изменение плавучести ПРК ( - оценка плавучести на рис. 1).
- оценка плавучести на рис. 1).
На рис. 2 представлены графики сигналов в контуре поршневого вытеснителя, полученные в результате моделирования системы управления (рис. 1) в управления (рис. 1) в среде Matlab.

Визуальный анализ показывает, что скважность работы исполнительного механизма приближается к 25, что является хорошим показателем автономности системы управления ПРК.
На рис. 2 представлены результаты идентификации постоянных времени объекта управления (T1)2 = 2000 и T2 = 40, также полученные в результате моделирования системы управления (рис. 1) в среде Matlab.
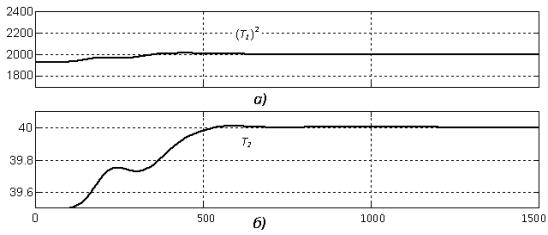
Рисунок 3. Графики подстройки постоянных времени T1 (а) и T2 (б)
Полученные результаты свидетельствуют о возможности точной и тонкой идентификации гидродинамических характеристик робото-технического комплекса.Таким образом, можно говорить, что определен путь решения двух задач, определяющих качество управления малогабаритными подводными аппаратами (роботами): задачи минимизации расхода электроэнергии силовым исполнительным механизмом и задачи идентификации гидродинамических параметров подводного аппарата, как объекта управления.
Список использованной литературы
1. Автономные необитаемые подводные аппараты. / Под общ. ред. М.Д.Агеева. – Владивосток: Дальнаука, 2000. – 272с.
2. Дьяконов В.П. Matlab 6.5 SP1/7 + Simulink 5/6. Основы применения.– М.: СОЛОН-Пресс, 2005. – 800 с.
3. Чураков Е.П. Оптимальные и адаптивные системы: Учеб. пособие для вузов. – М.: Энергоатомиздат, 1987. – 256 с.
4. Ивель В.П., Герасимова Ю.В. Моделирование системы стабилизации глубины погружения подводного аппарата // Матер. республик. науч.-практ. конфер. Петропавловск, 2006. – т. №1. – С. 72-76.
5. Кику А.Г., Костюк В.И., Краскевич В.Е. и др. Адаптивные системы идентификации. – Киев: техника, 1975. – 288 с.