Особенности идентификации параметров электромеханических вибровозбудителей с управляемымшим-преобразователем

Аннотация

Д.С. Пономарев - Особенности идентификации параметров электромеханических вибровозбудителей с управляемымшим-преобразователем. Исследование предварительной обработки данных перед параметрической идентификацией параметров вибровозбудителя виброустановки ВСОН-2100/2500 производства ПАО «Минэтэк» для снятия остаточных напряжений в металлах.

В настоящее время практически не существует инженеров и проектировщиков, которые не сталкивались с задачей идентификации объектов и систем. Как известно, данная задача базируется не только на аналитическом подходе, но и на интуитивном. И именно опыт и логическое мышление самого эксперта становятся ключом к разгадке «чёрного ящика».

Для проведения эксперимента на объекте можно воспользоваться различными методами и специализированными приборами [2], но одним из самых универсальных на данный момент является метод осциллографирования с применением современных средств сбора данных. Такой подход приводит к решению задачи обработки измеренных величин. Существует целый ряд методов, с помощью которых возможно обработать полученные сигналы [1, 3].

Для идентификации параметров вибровозбудителя был проведён целый ряд экспериментов, заключающийся в осциллографировании трёх основных сигналов: напряжения и тока на выходе широтно- импульсного модулятора (ШИМ) – преобразователя виброустановки и скорости двигателя постоянного тока вибровозбудителя дебалансного типа. Причиной создания алгоритмов послужило то, что управляемый преобразователь формировал ШИМ сигнал управления электродвигателем и в качестве датчика скорости использовался цифровой энкодер с количеством импульсов двадцать два на оборот вала. Естественно, процесс идентификации параметров затруднительно выполнить по импульсным сигналам, так как такие сигналы формируются дискретными функциями. Данные сигналы необходимо представить в виде средних значений за определённый период.

По результатам анализа принципов формирования импульсов скорости цифрового энкодера был разработан алгоритм перевода импульсного сигнала в сигнал среднего значения частоты оборотов на основе измерений времени периода и получен код для данного алгоритма в виде скрипта m-файла приложения Matlab. Основой алгоритма преобразования является программные триггер уровня и измеритель периода импульса. Триггер настраивается на величину амплитуды Utr в 25 % от высокого уровня. Он должен быть немного выше низкого уровня сигнала энкодера для отсечки шумовых составляющих. На рис. 1 проиллюстрирован процесс перевода импульсной функции в среднее значение скорости за период импульса энкодера.

Преобразованный сигнал, аналого-цифровое преобразование (АЦП), условно сдвинут по амплитуде ипредставлен в относительной форме.

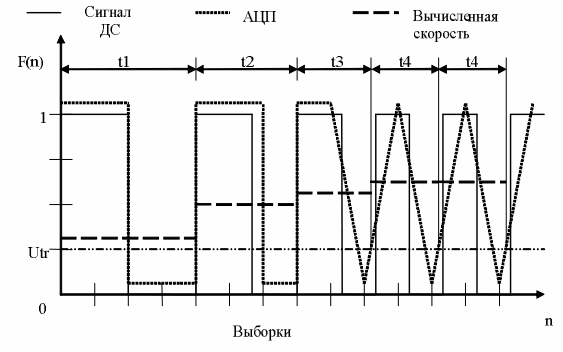
Рисунок 1. - Иллюстрация преобразования сигнала энкодера в частоту вращения

Сигнал с энкодера переводится из аналоговой формы в цифровую форму с помощью АЦП. Частота преобразования АЦП принята равной 5000 Гц, максимальная частота импульсов энкодера равна 2200 Гц. Импульсы треугольной формы, полученные в процессе преобразования, иллюстрируют процесс джиттера, который, несомненно, возникнет при оцифровке данных из-за асинхронной частоты выборок в процессе изменяющейся скорости двигателя. Искажение формы сигнала энкодера не влияет на алгоритм в связи с тем, что период преобразованного импульса с достаточной ошибкой не изменяется.

Алгоритм преобразования достаточно прост. Начальная скорость равна нулю. Происходит отслеживание заднего фронта импульса с одновременным измерением ширины импульса в выборках. При появлении амплитуды импульса с величиной, меньшей заданного значения триггера, устанавливается флаг низкого уровня. Далее происходит отсчёт выборок при низком уровне, которые прибавляются к количеству выборок высокого уровня. По достижении переднего фронта флаг обнуляется и производится расчёт средней скорости по величине измеренного периода в выборках с записью в массив средней величины скорости на измеренном участке. Далее величина периода импульса обнуляется, и процесс повторяется снова.

Для получения среднего значения напряжения и тока также применялись специализированные алгоритмы, работающие со средним значением величины за период такта ШИМ. Однако предварительно было выполнено сглаживание шумов методом скользящего среднего с шириной окна, равной 16 выборкам.

В процессе перевода значения напряжения изначально измерялся интервал в выборках периода ШИМ, далее вычислялось среднее значение напряжения за период и помещалось в массив выходной величины длиной в один период ШИМ. Также для выполнения расчёта среднего значения тока после измерения периода формировалась структура с метками начала и размера текущего периода ШИМ в выборках. Вычисление среднего значения тока аналогично напряжению, только информация о периоде бралась не из измерения, а из сформированной структуры для исключения фазового сдвига напряжения и тока в процессе влияния реактивных составляющих измеряемой цепи.

Полученные прямоугольные значения необходимо сгладить каким-либо методом. Для сравнения были выполнены сглаживания методом скользящего среднего с изменяемой шириной окна в начальных значениях до открытия полного окна, функцией filtfilt пакета Matlab и встроенным в него методом вейвлет- преобразований [4].

Функция фильтра второго порядка была настроена на частоту ШИМ, функции вейвлет-преобразования использовались для снятия шума, а ширина окна скользящего среднего для сглаживания скорости составляла в выборках частоту, эквивалентную частоте ШИМ. В стационарных режимах каждый из методов давал одинаковые результаты. Различие заключалось в динамических режимах, особенно в процессах пуска и торможения. Наиболее удовлетворительными характеристиками, на наш взгляд, обладал метод скользящего среднего. Фильтр и вейвлет-преобразование в динамических режимах показывали значительные изменения скорости вала двигателя. Данное утверждение можно охарактеризовать тем, что дискретные сигналы обладают бесконечно большим спектром сигнала и метод скользящего среднего является наиболее родственным таким сигналам. Именно поэтому он наиболее подходит для обработки сигналов ШИМ и цифровых энкодеров.

Фрагмент диаграммы пуска и работы по снятию напряжений в детали преобразователя вибровозбудителя после обработки измеренных сигналов представлен на рис. 2.

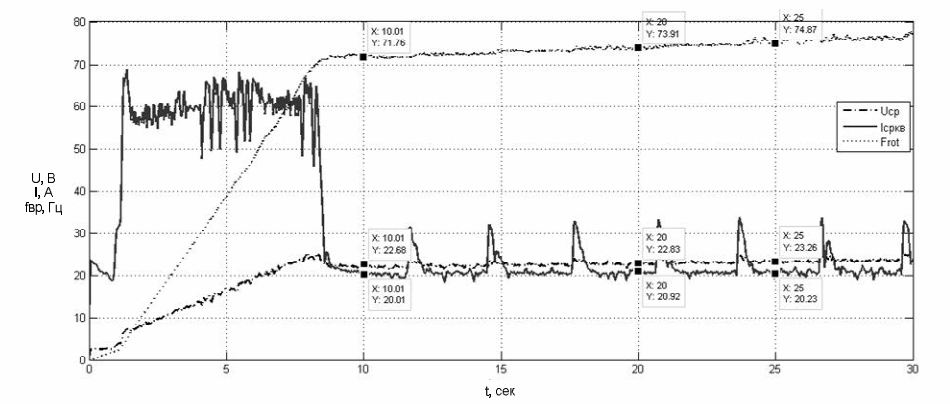
Рисунок 2. - Фрагмент диаграммы напряжения, тока преобразователя и частоты вращения двигателя после обработки импульсных сигналов преобразователя и датчика скорости

Выводы

Для реализации обработки импульсных сигналов и сигналов ШИМ с последующим получением среднего значения рекомендуется применять интегральные алгоритмы, одним из которых является скользящее среднее.

Список использованной литературы

1. Идентификация промышленных объектов и систем управления: учеб. пособие / В.М. Спасибов, И.А. Каменских, Ю.А. Ведерникова. – Ч. 1 – Тюмень: ТюмГНГУ, 2010. – 104 с.
2.Экспериментальное определение параметров и частотных характеристик автоматизированных электроприводов: библиотека по автоматике / Ю.А. Борцов, Г.В. Суворов, Ю.С. Шестаков. – Вып. 366 – Л.: Энергия, 1969. – 104 с.
3. Файнзильберг Л.С. Информационные технологии обработки сигналов сложной формы. Теория и практика. – К.: Наукова думка, 2008. – 333 с.
4. Яковлев А.Н. Введение в вейвлет-преобразования: учеб. пособие. – Новосибирск: Изд-во НГТУ, 2003. – 104 с.