Многомерное управление сушильным агрегатом
Автор:
Павленко А.А., Жукова Н.В.
Источник: СЕВЕРГЕОЭКОТЕХ–2013.
Сборник научных работ XIV Международной молодежной научной конференциии
— Ухта, УГТУ, 2013. — 440 с.
Автор:
Павленко А.А., Жукова Н.В.
Источник: СЕВЕРГЕОЭКОТЕХ–2013.
Сборник научных работ XIV Международной молодежной научной конференциии
— Ухта, УГТУ, 2013. — 440 с.
Сушильный агрегат, как объект управления имеет много входных и выходных технологических параметров, которые в той или иной мере используются для управления объектом и для контроля его функционирования. Главными технологическими управляемыми величинами сушильного агрегата являются производительность и влажность продукта на выходе агрегата. Для поддержания процесса сушки в оптимальном режиме требуется поддерживать соотношение газ/воздух в горелке.
Рассмотрим технологию сушки с точки зрения управления процессом. В процессе работы сушильного агрегата на него действуют управляющая величина (подача газа), возмущения (скорость подачи влажного материала в печь) и другие воздействия такие, как подача воздуха для поддержания необходимой температуры сушильного агента и для оптимального горения топки. Производительность сушилки, как главная входная величина и главная выходная величина, является с точки зрения управления сушкой, возмущением. Влажность материала на входе также является возмущением, так как она не может регулироваться при управлении непосредственно сушильным агрегатом.
В результате, сушильный агрегат, как объект управления, может быть представлен такой структурно-функциональной моделью (рис. 1).

Рисунок 1. Структурно функциональная схема сушильного агрегата
Существующие системы управления сушильным агрегатом, представляющим собой многомерный многосвязный объект, построены в виде иерархической структуры, состоящей из параллельно, одновременно работающих и связанных локальных САР. Внешней, по отношению к процессу сушки, является САР производительности, задание для которой определяется оператором или технологией. Остальные САР обеспечивают качество процесса сушки. Главная из них обеспечивает требуемую влажность материала на выходе, вспомогательная – оптимизирует процесс горения и сушки. Разрабатывается математическая модель объекта по каждому каналу и проводится оптимизация параметров элементов контуров так же, как это делается для объекта с одной управляющей и одной управляемой величинами. Оценивается перекрестное влияние управляющих величин при параллельной работе всех САР и, при необходимости, уточняются настройки регуляторов, исключая потенциальную возможность перехода САР в неустойчивое состояние.
Анализ вопроса автоматизации процессов сушки показал, что существующие классические локальные САР не в полной мере учитывают многомерность и многосвязность данного процесса, и поэтому есть необходимость применить современные методики синтеза многомерных робастных регуляторов, синтез которых требует математическое описание многомерного объекта в терминах переменных состояния.
Однако, процессы сушки относятся к объектам с элементами запаздывания, поэтому при описании математической модели в терминах переменных состояния необходимо учитывать то, что каждая переменная состояния исходной модели, не учитывавшей задержки, может быть задержана на некоторое время соответствующим звеном запаздывания. Поэтому набор переменных состояния уравнения динамики должен быть дополнен таким же числом переменных состояния, соответствующих выходным сигналам звеньев запаздывания. Для реализации вышесказанного придется ввести формальный оператор [1], описывающий значение функции, опережающее по времени текущее на интервал τ. Для задач, решаемых в реальном времени, такой оператор-предсказатель, естественно, нереализуем. Но для апостериорного решения [2, 3], когда воздействия известны заранее на всем нужном промежутке времени, это возможно. Тем более, что проводимое описание направлено на получение в результате модели объекта с запаздыванием, способной работать в реальном времени, составляемой на основе уравнения состояния.
Целью статьи является обеспечение заданного влагосодержания при текущей производительности установки за счет разработки многомерного робастного регулятора. Методология синтеза вышеназванного регулятора позволяет отнести системы управления, построенные на таком принципе, к оптимальным системам, в которых оптимизация проводится по некоторому заданному квадратичному критерию качества. Также эта теория принимает в расчёт возможность изменения параметров объекта в процессе функционирования и учитывает помехи измерительных устройств, действующие в цепи возмущений и измерений в виде белого гауссовского шума (БГШ).
Рассматривается модель объекта управления в пространстве состояний с учетом запаздывания и шумов в цепи измерения и управления:
 (1)
(1)
где 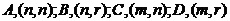 - матрицы
динамики, управления и измерения соответственно;
- матрицы
динамики, управления и измерения соответственно;  - БГШ со следующими
характеристиками:
- БГШ со следующими
характеристиками:

Функционал качества оптимального управления можно представить в виде:
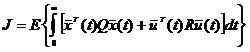 (2)
(2)
где 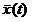 - вектор состояния
объекта управления,
- вектор состояния
объекта управления,  - симметричные
положительно-определенные матрицы коэффициентов веса по переменным
состояния и управляющим воздействиям.- симметричные
положительно-определенные матрицы коэффициентов веса по переменным
состояния и управляющим воздействиям.
- симметричные
положительно-определенные матрицы коэффициентов веса по переменным
состояния и управляющим воздействиям.- симметричные
положительно-определенные матрицы коэффициентов веса по переменным
состояния и управляющим воздействиям.
Синтез робастного линейно - квадратического гауссовского регулятора (LQG-регулятора) включает две задачи: cинтез оптимального регулятора состояния по критерию (2); синтез наблюдателя состояния, учитывающий помехи, действующие на объект, так называемый фильтр Калмана.
Параметры фильтра Калмана
определяются однозначно, если известны статистические характеристики
помех, воздействующих на объект и (или) искажающих результаты
измерений. Фильтр Калмана минимизирует среднеквадратическую ошибку
оценки состояния системы: 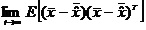 . Тогда, истинный
вектор состояния объекта
. Тогда, истинный
вектор состояния объекта 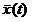 заменяется на
восстановленный
заменяется на
восстановленный 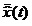 и исходная задача
может быть сведена к классической задаче LQR – управления [4].
и исходная задача
может быть сведена к классической задаче LQR – управления [4].
Структурная схема фильтра представлена на рис.2.
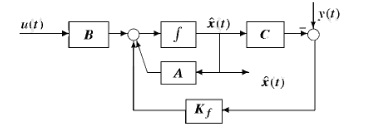
Рисунок 2. Структурная схема фильтра Калмана
Здесь 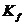 матрица
коэффициентов фильтра, определяется следующим образом:
матрица
коэффициентов фильтра, определяется следующим образом:
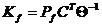 (3)
(3)
где  симметричная
положительно-определенная матрица, т.е.
симметричная
положительно-определенная матрица, т.е. 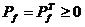 удовлетворяет
алгебраическому уравнению Риккати:
удовлетворяет
алгебраическому уравнению Риккати:
 (4)
(4)
После получения оптимальной
оценки состояния 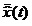 структурную схему
замкнутой системы с LQG – регулятором можно представить на
рис.3 с оптимальным управлением:
структурную схему
замкнутой системы с LQG – регулятором можно представить на
рис.3 с оптимальным управлением:  и матрицей
коэффициентов обратной связи по состоянию оптимального LQR -
регулятора
и матрицей
коэффициентов обратной связи по состоянию оптимального LQR -
регулятора  .
.
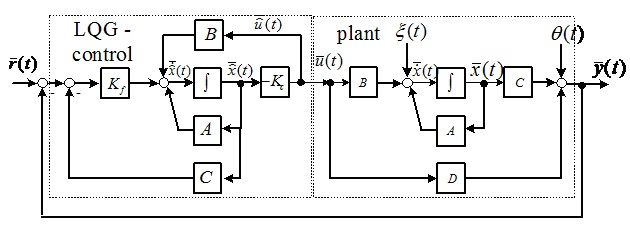
Рисунок 3. Структура замкнутой системы с LQG – регулятором
Отсюда следует, что в LQG - оптимальном управлении задачи оптимальной оценки состояния объекта и оптимального управления решены раздельно (по так называемому «принципу разделения»). Т.е, сначала синтезируется фильтр Калмана и на полученной оценке состояния, как если бы вектор состояния точно измерялся, проектируют оптимальный LQR –регулятор.
1. Технологический процесс сушки, представленный как объект управления с элементами запаздывания, является многосвязным и многомерным. Применение современных методик синтеза многомерных робастных регуляторов требует получение модели многомерного объекта с запаздыванием на основе уравнений состояния, способной работать в реальном времени.
2. При синтезе САУ многомерным объектом будет применена методика оптимального ЛКГ - управления, учитывающая возможные изменения параметров объекта в процессе функционирования, неточность модели и помехи средств измерения и возмущения.
1. Model.Exponenta.Ru — учебно-методический сайт о моделировании
и исследовании систем, объектов, технических процессов и физических
явлений. http://model.exponenta.ru/
2. Лукас В.А. ТАУ. Изд. 3-е. Изд. УГГГА, Екатеринбург, 2002, –
675 стр
3. Ким. Д.П. Сборник задач по теории автоматического управления.
Многомерные, нелинейные, оптимальные и адаптивные системы. – М.:
ФИЗМАТЛИТ, 2008. – 328с.
4. Xue, Dingyü, Chen, YangQuan, and Atherton, Derek P., Linear
feedback control: Analysis and design with MATLAB.