Автоматическое регулирование технологических процессов: учебное пособие (Издание второе)

В. Ф. Комиссарчик (стр. 339-341)

8.1. Формулировка задачи оптимального управления

Задача синтеза многомерного регулятора в пространстве состояния формализуется обычно в виде задачи о максимальной точности с интегральным квадратичным функционалом I:

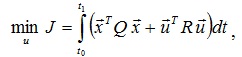(249)

где   – соответственно начальное и конечное время,

– интервал управления (при 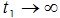 имеем бесконечный интервал управления),

– вектор переменных состояния системы размерностью n (n– вектор);

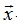– вектор переменных управления;

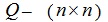– квадратная положительно определенная диагональная матрица весовых коэффициентов состояния;

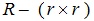– квадратная положительно полуопределенная диагональная матрица весовых коэффициентов управления.

Вообще говоря, в критерии задачи (249) вместо вектора состояния 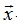 следовало бы писать отклонение вектора состояния от его заданного значения 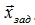. Однако для упрощения записи полагаем 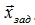=0.

Размерность вектора состояния равна порядку дифференциального уравнения (системы уравнений), которыми описывается данная динамическая система.

Первое слагаемое (квадратичная форма матрицы Q) вводится в критерий задачи (249) с целью минимизации суммы интегральных квадратичных критериев для переменных состояния взятых с весовыми коэффициентами равными элементам матрицы Q.

Второе слагаемое в критерии задачи (249) (квадратичная форма матрицы R) позволяет минимизировать сумму квадратичных интегральных критериев для переменных управления взятых с весами равными элементам матрицы R и таким образом ввести ограничения на управление.

Поскольку многомерные регуляторы проще всего реализовать с помощью цифровых вычислительных устройств, перейдем к дискретному аналогу задачи (249):

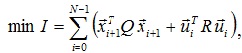 (250)

где N– число периодов квантования по времени в интервале управления.