Разработка управляющих программ промышленных роботов

Аннотация

А.С. Климчик Р.И. Гомолицкий Ф.В. Фурман К.И. Сёмкин - Разработка управляющих программ промышленных роботов. Предложено и исследовано несколько вариантов построения модели сферического движения твердого тела с неподвижным центром вращения. Получено условие устойчивого сферического движения твердого тела. Выведены уравнения малых колебаний тела при его устойчивом сферическом движении.

Матрицу поворота размерностью 3x3 можно определить как матрицу преобразования трехмерного вектора положения в евклидовом пространстве, переводящую его координаты из повернутой(связанной) системы отсчета OUVW в абсолютную систему координат OXYZ. На Рис. 1 показаны две правые прямоугольные системы координат: системы координат OXYZ с осями OX, OY, OZ и система OUVW с осями OU, OV, OW. Начала этих систем совпадают и расположены в точке О. Система OXYZ фиксирована в трехмерном пространстве и принята за абсолютную, а система координат OUVW вращается относительно абсолютной системы OXYZ. Физически система OUVW может рассматриваться как связанная система, координат. Это означает, что она соответствующим образом жестко связана с твердым телом (например, с летательным аппаратом или звеном манипулятора) и движется вместе с ним. Пусть (ix,jy,kz) и (iu,jv,kw) — единичные векторы, направленные вдоль осей систем OXYZ и OUVW соответственно. Некоторую точку p в пространстве можно охарактеризовать координатами относительно любой из указанных систем. Для простоты рассуждений предположим, что точка р фиксирована и неподвижна в системе отсчета OUVW. Тогда в системах координат OUVW и OXYZ точка будет иметь соответственно координаты

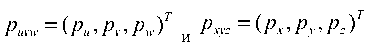
где puvw и pxyz характеризуют положение одной и той же точки p относительно различных систем отсчета. Верхний индекс T , добавляемый к обозначению вектора или матрицы, обозначает операцию транспонирования.

Наша задача состоит в том, чтобы определить матрицу R размерностью 3x3 , которая преобразует координаты puvw в координаты вектора p в системе OXYZ после того, как система OUVW будет повернута, т. е.

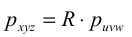
Заметим, что физически точка р вращается вместе с системой координат OUVW.

Из определения компонент вектора имеем

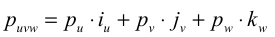
где pu, pv и pw представляют собой составляющие вектора p вдоль осей OU, OV и OW соответственно, или проекции вектора p на эти оси. Таким образом, используя определение скалярного произведения и равенство (3), получаем

или в матричной форме

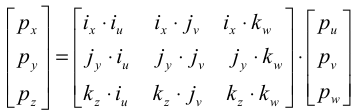
С учетом этого выражения матрица R в равенстве (2) примет вид

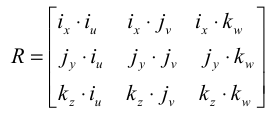
Аналогично, координаты puvw , можно получить из координат pxyz :

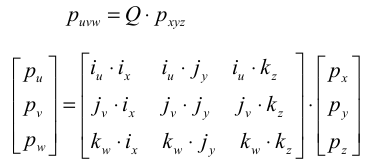
Поскольку операция скалярного произведения коммутативна, то из соотношений (6) — (8) следует

где I3 — единичная матрица размерностью 3x3 . Преобразование, определяемое формулой (2) или (7), называется ортогональным преобразованием, а поскольку все векторы, входящие в скалярные произведения, единичные, его также называют ортонормальным преобразованием.

Особый интерес представляют матрицы поворота системы OUVW относительно каждой из трех основных осей системы OXYZ. Если положение системы OUVW в пространстве изменяется за счет поворота этой системы на угол а вокруг оси ОХ, то в системе отсчета OXYZ изменятся и координаты (px,py,pz)^T точки puvw , имеющей в системе OUVW неизменные координаты (pu,pv,pw). Соответствующая матрица преобразования Rx,α а называется матрицей поворота вокруг оси ОХ на угол α. Основываясь на полученных выше результатах, для матрицы Rx,α имеем

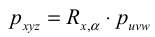
причем iu=ix, и

Аналогично, трехмерные (размерностью 3x3 ) матрицы поворота вокруг оси OY на угол φ в вокруг оси OZ на угол θ имеют соответственно вид Рис. 2.

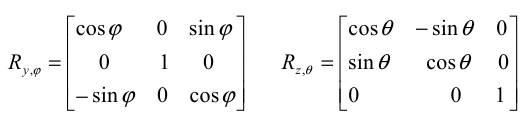
Матрицы Rx,α ,Ry,φ , и Rz,θ называются матрицами элементарных поворотов. Любые другие матрицы конечных поворотов можно получить, используя матрицыэлементарных поворотов.

Пример.

Требуется найти матрицу поворота, являющегося результатом последовательного выполнения поворотов сначала на угол φ вокруг оси OY, затем на угол θ вокруг оси OW и на угол α вокруг оси OU.

Решение