
УДК 621.373.1
А.Г.
Воронцов (д.т.н, проф.), А.А. Полапа
Донецкий
национальный технический университет,
г. Донецк
кафедра автоматики и
телекоммуникаций
E-mail:
_vag_@mail.ru,
polapa-andrew@yandex.ua
РАЗРАБОТКА ГЕНЕРАТОРА ИМПУЛЬСНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ ДЛЯ ИЗМЕРИТЕЛЯ ЧАСТОТЫ
Источник: Сборник научных трудов Донецкого национального технического университета (факультет КИТА), серия: «Вычислительная техника и автоматизация». – 2013. – Вып. 21(183). – С.112-117.
Выполненообоснованиеформы
импульса,
отличной отпрямоугольной,
при моделировании сигналов в
телекоммуникационных системах для
учета возникающей погрешности, играющей
важную роль в оценке моделей методов
высокоточного измерения частоты.
Предложено использование такого
представления сигнала для моделирования
измерителя частоты на основе рациональных
приближений. Разработаны модели
генератора импульсных последовательностей
с учетом выдвинутых требований в таких
программных пакетах, как SystemView
и MatLab. Проведен сравнительныйанализ
ивыбрана
наилучшая
реализация.
Ключевые
слова:генератор
импульсных последовательностей, метод
рациональных приближений, моделирование,
SystemView,
MatLab, фронт импульса.
Общая постановка проблемы.
В телекоммуникационных системах и системах связи частотные измерения получили широкое распространение. Они являются обычным инструментом при решении задач диагностики, оптимизации, разработки, технического обслуживания и т.д. Требования к методам и средствам частотных измерений определяются спецификой технического объекта, особенностями его использования и в некоторых случаях могут быть противоречивы. Так, например, при диагностировании джиттера необходимо обеспечить высокую точность измерения частоты при ограниченном по длительности интервале измерения. Ограничение по времени не позволяет использовать усреднение как универсальное и эффективное средство повышения точности измеряемой частоты.
Стандартные методы измерения частоты могут обеспечивать минимальную погрешность и даже теоретическое отсутствие систематической погрешности. Условия наступления такого события для каждого из методов свои, но в их основе лежит кратность измеряемой и эталонной частоты, на основе которой производится измерение. Проблема заключается в том, что такие ситуации являются уникальными, маловероятными и не могут рассматриваться как стандартные. Однако существует и другой подход к решению задачи измерения частоты за ограниченный промежуток времени с максимизацией точности. Идея заключается в подборе временной базы измерения, кратной измеряемому периоду, в результате чего за время измерения наблюдается целое число периодов неизвестной частоты. Таким образом, сводится к минимуму методическая погрешность и теоретически она равна нулю. Примером такого подхода является метод измерения частоты с помощью рациональных приближений. Формирование и обоснование концепции измерителя частоты на основе рациональных приближений приведено в [1]. Целью приведенной работы является повышение точности измерений в условиях ограничения по времени, т.е. в определенной степени решение проблемы ограничения «погрешность – время измерения». Однако для исследования и оценки корректности работы метода в реальных условиях очень важна степень соответствия исходного сигнала, используемого в качестве входного в модели измерителя частоты, реальному сигналу, присутствующему в телекоммуникационных системах, и наличие целого ряда характерных особенностей, таких как конечная скорость нарастания фронта, наличие фазовой нестабильности (джиттера). Так, на качество измерения при практической реализации большое влияние оказывают ширина импульсов в последовательности и их фронты, наличие которых приводит к ложному учету (или неучету) периода при их подсчете. Кроме того, воздействие помех на реальные импульсы с пологим фронтом приводит к возникновению явления джиттера, т.е. фазовой нестабильности положения импульса.
Для разработки методов и средств измерения частоты в этих условиях необходимо изучить специфику формирования погрешности измерения частоты с учетом влияния формы импульсов. Как средство исследования предполагается использование моделирования. Однако моделирование также сопряжено с погрешностями, присущими выбранным методам и средствам.
Постановка задач исследования.
Целью данной работы является снижение погрешности моделирования сигналов генератора импульсных последовательностей заданной частоты за счет более детального представления формы импульса.
Для достижения поставленной цели необходимо решить следующие задачи:
Обосновать необходимость учета непрямоугольной формы импульсов при моделировании.
Решение задач и результаты исследований.
Первоначальное оценивание метода измерения частоты на основе рациональных приближений допускает значительное идеализирование условий, в т.ч. и формы импульса [2]. Однако более детальная оценка метода, приближенная к реальным условиям функционирования, требует учета реальной формы импульса, т.к. учет степени перекрытия, на которую влияет форма фронта импульса, может играть важную роль в оценке погрешности. Кроме того, в реализации данного метода фигурирует понятие «узкого импульса». Это свидетельствует о том, что длительности переднего и заднего фронтов относительно длительности всего импульса являются достаточно значимыми величинами для того, чтобы ими не пренебрегать.
Для обоснования всей последующей работы необходимо оценить требования к методам измерения частоты при диагностировании джиттера. Как вариант сравнения рассмотрим известный метод прямого счета (см. рис. 1).

Рисунок 1 – Структурная схема простейшего частотомера, реализующего концепцию прямого счета.
Для
определенности примем, что
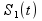 – сигнал с неизвестной частотой
– сигнал с неизвестной частотой
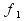 ,
,
 – эталонный сигнал, частота которого
известна
– эталонный сигнал, частота которого
известна
 .
Измерение частоты предполагает, что
.
Измерение частоты предполагает, что
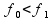 .
При реализации метода прямого счета
требование обеспечения высокой точности
приводит к условию
.
При реализации метода прямого счета
требование обеспечения высокой точности
приводит к условию
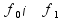 ,
что в свою очередь определяет минимальное
время измерения
,
что в свою очередь определяет минимальное
время измерения
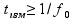 и относительную погрешность:
и относительную погрешность:
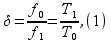
– где
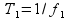 и
и
 – период измеряемого и эталонного
колебания, соответственно.
– период измеряемого и эталонного
колебания, соответственно.
Если
принять, что
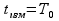 ,
то для получения погрешности измерения
не больше заданной
,
то для получения погрешности измерения
не больше заданной
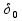 требуемые временные затраты составят:
требуемые временные затраты составят:
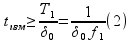
В
современных телекоммуникациях часто
приходится иметь дело с периодическими
сигналами с частотой в единицы МГц при
допустимой нестабильности частоты
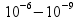 .
При использовании частотных измерений
для диагностирования периодического
джиттера относительная погрешность
измерений существенно меньше указанной
нестабильности. Для грубой, чисто
качественной оценки времени измерения
примем, что эти величины равны. Тогда
для частоты
.
При использовании частотных измерений
для диагностирования периодического
джиттера относительная погрешность
измерений существенно меньше указанной
нестабильности. Для грубой, чисто
качественной оценки времени измерения
примем, что эти величины равны. Тогда
для частоты
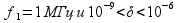 имеем время измерений
имеем время измерений
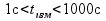 .
Если причиной джиттера является наводки
со стороны промышленной сети,
.
Если причиной джиттера является наводки
со стороны промышленной сети,
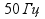 (
(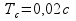 ),
то за время измерения частота измеряемого
сигнала изменится многократно и
результатом измерения будет ее среднее
значение и джиттер обнаружить не удастся.
),
то за время измерения частота измеряемого
сигнала изменится многократно и
результатом измерения будет ее среднее
значение и джиттер обнаружить не удастся.
Не решает проблемы и переход от измерения частоты к измерению периода, неопределенность по количеству подсчитанных импульсов преобразуется в неопределенность по длительности временного интервала. Погрешность определяется по той же формуле (1).
Использование
метода рациональных приближений
предоставляет возможность получить
предельно малое значение погрешности
измерений, по крайней мере для ограниченного
множества частот, да и то только
теоретически. В основе метода лежит
сравнение последовательностей «узких»
импульсов на компараторе (см. рис. 2). Для
минимизации ошибки измерений необходимо,
чтобы существовало некоторое число
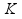 ,
общее кратное для частот
,
общее кратное для частот
 и
и
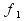 ,
а сигналы
,
а сигналы
 и
и
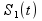 представляли собой последовательности
представляли собой последовательности
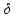 –функций.
–функций.

Рисунок 2 – Структурная схема простейшего частотомера, реализующего концепцию рациональных приближений.
Эти условия можно сформулировать в виде:
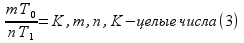
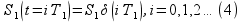
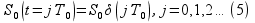
Условие
(3) означает, что в
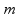 периодах эталонной частоты
периодах эталонной частоты
 укладывается ровно
укладывается ровно
 периодов измеряемой частоты
периодов измеряемой частоты
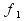 .
В реальности это условие выполняется
только с некоторой степенью приближения,
чему способствует увеличение отношения
.
В реальности это условие выполняется
только с некоторой степенью приближения,
чему способствует увеличение отношения
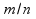 .
Неизбежным негативным следствием
последнего является увеличение времени
измерения
.
Неизбежным негативным следствием
последнего является увеличение времени
измерения
 (здесь величина
(здесь величина
 может быть значительно меньше одноименной
величины в формуле (1)). Но даже если
предположить, что условие (3) выполняется
точно, невыполнимость условий (4) и (5) не
позволяют достигнуть идеального
результата. Импульсы реальных сигналов
всегда имеют конечную длительность,
поэтому возникает неопределенность с
моментом совпадения этих импульсов во
времени. Для первого приближения примем,
что сигналы
может быть значительно меньше одноименной
величины в формуле (1)). Но даже если
предположить, что условие (3) выполняется
точно, невыполнимость условий (4) и (5) не
позволяют достигнуть идеального
результата. Импульсы реальных сигналов
всегда имеют конечную длительность,
поэтому возникает неопределенность с
моментом совпадения этих импульсов во
времени. Для первого приближения примем,
что сигналы
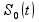 и
и
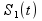 – последовательности узких прямоугольных
импульсов одинаковой длительности
– последовательности узких прямоугольных
импульсов одинаковой длительности
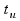 и с частотами следования
и с частотами следования
 и
и
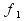 ,
соответственно (см. рис. 3).
,
соответственно (см. рис. 3).
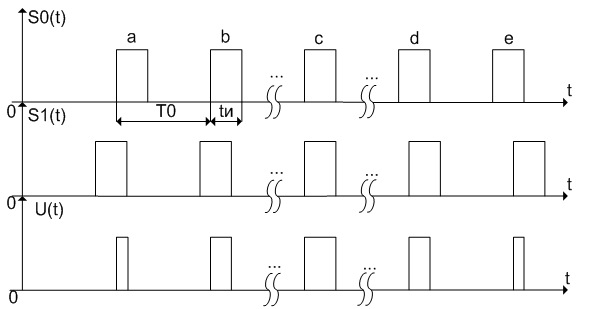
Рисунок 3 – Временная диаграмма сигналов в частотомере рациональных приближений.
Как
видно из рисунка 3 при функционировании
частотомера полные совпадения импульсов
последовательностей
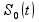 и
и
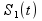 только частный случай (позиция
только частный случай (позиция
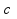 ).
Возможны другие комбинации с разной
степенью перекрытия импульсов. Как
видно из построения, сигнал
).
Возможны другие комбинации с разной
степенью перекрытия импульсов. Как
видно из построения, сигнал
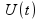 ,
используемый для формирования управления
счетчиком
,
используемый для формирования управления
счетчиком
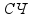 ,
имеет нестабильные фронты (передний и
задний фронты «мигрируют» в зависимости
от степени перекрытия
,
имеет нестабильные фронты (передний и
задний фронты «мигрируют» в зависимости
от степени перекрытия
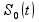 и
и
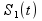 ).
Это приводит к временной неопределенности,
равной длительности импульса
).
Это приводит к временной неопределенности,
равной длительности импульса
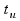 ,
и погрешности измерения длительности
периода
,
и погрешности измерения длительности
периода
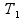 :
:
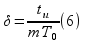
Как
видно из (6), при одинаковых затратах
времени на измерение, единственной
мерой понижения погрешности является
укорочение длительности импульсов
последовательностей
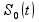 и
и
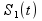 .
Другим негативным фактором является
неоднозначность
.
Другим негативным фактором является
неоднозначность
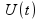 ,
поскольку при конечной длительности
,
поскольку при конечной длительности
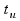 при постоянном набеге разности фаз
сигналов
при постоянном набеге разности фаз
сигналов
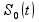 и
и
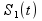 имеет место постоянное «наползание»
сигнала
имеет место постоянное «наползание»
сигнала
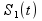 на
на
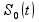 за несколько смежных периодов
за несколько смежных периодов
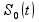 .
Таким образом, вместо однократного
совпадения и одиночного импульса
.
Таким образом, вместо однократного
совпадения и одиночного импульса
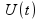 имеем последовательность
имеем последовательность
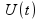 с изменяющимися положениями фронтов.
Попытка выделить единственный импульс
«полного совпадения» не представляется
простой, если учесть как отличие реальной
формы импульсов от прямоугольной, так
и зашумленность реальных сигналов.
с изменяющимися положениями фронтов.
Попытка выделить единственный импульс
«полного совпадения» не представляется
простой, если учесть как отличие реальной
формы импульсов от прямоугольной, так
и зашумленность реальных сигналов.
Пожалуй, единственной реальной возможностью разобраться во всем этом является хорошо обоснованное корректное моделирование, количественно описывающее все факторы, которые здесь рассмотрены лишь качественно. И в первую очередь это относится к приближению формы импульсов к реальной (например, трапецеидальной) и к учету действия помех.
Сформулируем требования к генератору импульсных последовательностей. Во-первых, генерируемая частота должна быть легко настраиваемой. Во-вторых, должна присутствовать возможность регулировать точность представления импульса, т.е. изменять количество отсчетов за период. В-третьих, фронты импульса должны обладать конечной настраиваемой скоростью нарастания, при этом наклон переднего и заднего фронтов могут быть разными, что характерно для реальных систем.
В качестве сред моделирования рассмотрим наиболее популярные и предоставляющие пользователю широкий круг возможных решений – SystemView by ELANIX и MatLab. Данные программные продукты во многих аспектах направлены на решение сходных задач, однако в них реализованы различные подходы, что и обусловило их выбор для решения поставленной задачи.
Для
формирования импульсной последовательности
с заданными требованиями в программном
пакете System
View
v5.0
Build
046 средствами среды была разработана
модель генератора с возможностью
регулирования скорости нарастания
фронта. Особенностью пакета является
необходимость настройки системного
времени. Данный инструмент требует
достаточно точного регулирования с
учетом ряда требований, в т.ч. и выполнения
условий, вытекающих из теоремы
Котельникова. Однако возможность такой
тонкой настройки позволяет с требуемой
точностью регулировать количество
отсчетов за период сигнала, а также
длительность реализации. Так, к
настраиваемым параметрам относятся
начальное время моделирования, конечное
время моделирования, шаг дискретизации
по времени, количество отсчетов за время
моделирования, частота формирования
отсчетов, разрешение по частоте,
количество циклов моделирования.
Разработанный генератор представлен
на рисунке 4.
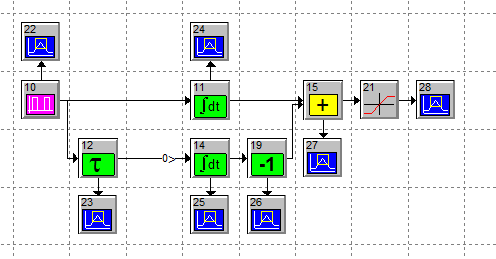
Рисунок 4 – Генератор импульсных последовательностей в SystemView.
Разберем предназначение блоков модели более детально. Блок 10 служит для формирования импульсной последовательности, состоящей из идеальных импульсов. Особенности работы программного пакета обуславливают наличие фронта даже в данном случае. Однако он формируется вследствие интерполяции соседних отсчетов. Таким образом, скорость нарастания фронта напрямую зависит от количества отсчетов за период, что делает невозможным как задание наклона фронтов напрямую, так и независимость от настроек системного времени и частоты сигнала, что недопустимо. При задании параметров в блоке можно указывать ширину импульса, его амплитуду и частоту повторения импульсов последовательности. Блок 12 – блок задержки сигнала, равен ширине импульса. Используется как промежуточное звено для формирования последовательности треугольных импульсов. Элементы 11 и 14 являются интеграторами. Они накапливают значение сигнала при передаче единичного уровня и сохраняют его значение при передаче нулевого уровня. В дальнейшем интересует лишь момент начала накопления и время накопления. Элемент 19 – инвертор. После его прохождения мы получаем два сигнала, противоположных по знаку и смещенных один относительно другого на длительность импульса. Блок 15 представляет собой сумматор. За счет суммирования сигналов с интеграторов получаем последовательность треугольных импульсов. Блок 21 – ограничитель. Он срезает пики треугольников, позволяет сформировать импульсы трапецеидальной формы, т.е. обладающие неидеальными фронтами. Графики, отображающие сигналы на выходах различных блоков модели, представлены на рисунке 5.
Скорость нарастания фронта можно регулировать амплитудой исходной импульсной последовательности (блок 10). Соотношение участков нарастания и максимального значения импульса можно регулировать посредством блока 21.
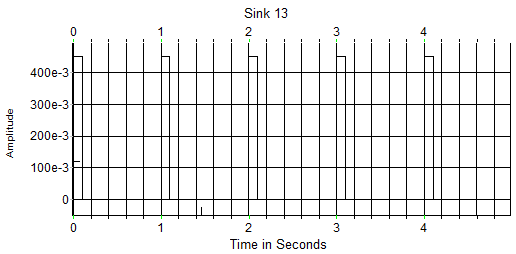
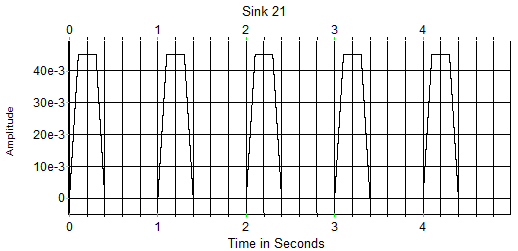
Рисунок 5 – Графики исходного сигнала для моделирования а) и сигнала на выходе генератора б).
К плюсам данной модели можно отнести простоту настройки частоты последовательности, наглядность предоставляемой информации и удобство регулирования точности представления импульсов. Однако разработанный генератор обладает и рядом недостатков. Так, сложно регулировать скорость нарастания фронтов и невозможно установить разные наклоны переднего и заднего фронта. Кроме того, изменение ширины импульсов требует изменения настроек ряда блоков модели.
Названные недостатки были учтены и устранены при создании модели в пакете MatLab. Стандартные средства среды моделирования Simulink не позволяют создать генератор импульсов задаваемой формы определенной частоты с регулируемой точностью представления. Поэтому необходимо дополнить и объединить существующие блоки для достижения поставленной задачи.
Модель состоит из блока задания формы импульсов (см. рис. 6) и фрагментов кода для установки частоты и задания длины последовательности. Блок Signal Builder позволяет формировать импульс с задаваемыми фронтами и длительностью на определенном временном интервале, кратном 10. Наиболее удобно для последующего масштабирования выбрать интервал 1с. При этом возможно изменение количества отсчетов за один период генерируемого сигнала, что позволяет регулировать точность представления.
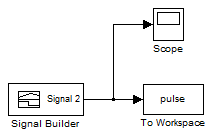
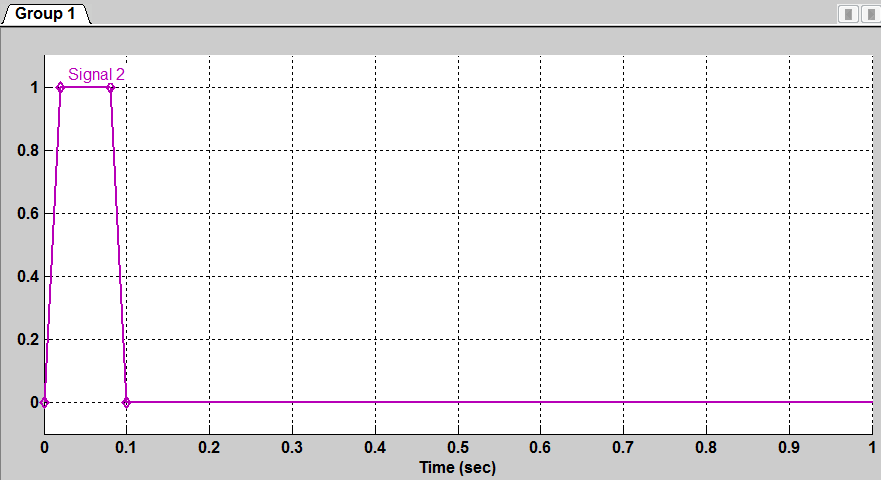
Рисунок 6 – Блок задания формы импульсов
Сформированный
сигнал экспортируется в рабочую область
в виде структуры pulse, содержащую в себе
матрицу отсчетов времени и матрицу
значений амплитуд. Следующим шагом
является выполнение подпрограммы
формирования требуемой частоты (см.
рис. 7). Пользователь выбирает нужную
частоту, затем производится обработка
массива отсчетов времени и период,
равный 1с сигнала с блока задания формы
импульсов преобразуется в период
заданной частоты.

Рисунок 7 – Блок формирования требуемой частоты.
На следующем этапе необходимо увеличить количество периодов сигнала до уровня, обоснованного проводимыми исследованиями (см. рис. 8). Для этого производится конкатенация массива данных заданное количество раз, а массив отсчетов времени последовательно увеличивается.

Рисунок 8 – Блок увеличения количества периодов.
К плюсам данной реализации генератора импульсных последовательностей можно отнести возможность тонкой настройки формы импульса, установки разной скорости нарастания фронтов. Количество отсчетов за период сигнала и частота сигнала легко изменяются. Недостатки модели включают в себя необходимость модернизации и изменения существующих блоков MatLab, что повышает вероятность ошибки, более сложную работу с системным временем.
Наиболее полно удовлетворяет выдвинутым требованиям модель, реализованная средствами MatLab, т.к. в ней наиболее точно можно задать форму импульса и точность его представления, что для поставленной цели является самым важным фактором. Более простая реализация в SystemView полностью нивелируется сложностью точной настройки формы импульсов и задания скорости нарастания фронта. Исходя из этого, для дальнейшего моделирования измерителя частоты на основе рациональных приближений была выбрана реализация генератора импульсных последовательностей в MatLab, как наиболее полно отображающая важные составляющие исследуемого сигнала.
Выводы.
Список использованной литературы
Полапа А.А. Анализ и обоснование методов измерения частоты колебаний в условиях ограничения «время – погрешность измерений» / А.А. Полапа // Мат. 9-й Междунар. молодежной научно-технической конф. «Современные проблемы радиотехники и телекоммуникаций» (РТ-2013). — Севастополь: Изд-во СевНТУ, 2013. — С. 158 — 159.
Daniel Hernández Balbuena, Oleg Sergiyenko, Vera Tyrsa, Larysa Burtseva, Moisés Rivas López, Signal frequency measurement by rational approximations, Measurement, vol. 42, no. 1, Elsevier, 2009, pp. 136–144.
Надійшла
до редакції: Рецензент:
01.04.2013
р. д.т.н, проф. Зорі
А.А.
A.G.
Vorontsov, A.A.
Polapa.
Development of pulse sequences generator for frequency meter. In
telecommunication systems, one of the fundamental problems is to
perform accurate measurements of the frequency for a limited period
of time, such as for the diagnosis of jitter. Increasing the
measurement interval results in smoothing obtained characteristics
and loss of high-frequency jitter components, resulting in reduced
accuracy. Thus is formed the problem of limiting "error - the
measurement time", i.e. obtaining high-frequency values in
a relatively short time intervals. The justifications of the use of
non-ideal shape of the pulse in the signals’ simulation in
telecommunication systems to account for the uncertainty arising,
which plays an important role in the evaluation of models for
high-precision measurement of frequency. Proposed the use of the
signal representation for modeling the frequency meter based on
rational approximations. Formed the requirements for the generator
pulse sequences, such as simple setting of generated frequency, the
possibility of regulation the accuracy of representation of the
impulse (possibility of changing the number of samples per cycle),
the independence of setting the front and rear edges. Developed model
of the pulse sequences with the requirements in such software
packages as SystemView by ELANIX and MatLab. A comparative analysis
of models, noted the benefits and drawbacks. Thus, the model in
SystemView is simple during the frequency’s regulation of the
sequence, has good representation of the information and is not very
complex to regulate the accuracy. But it has a critical drawback -
it is difficult to adjust the rate of growth of the fronts and you
can not configure them separately. On the other hand, the model in
MatLab having the above-mentioned advantages and eliminating the main
disadvantages. Elements of the code were given and generated on the
basis of them the function block diagram of the model. Thus, based on
the analysis model of the generator, implemented in MatLab, was found
to be more optimal in terms of stated goals and
objectives.
Keywords:
pulse sequences generator, the method of rational approximation,
simulation, SystemView, MatLab, wavefront.
О.Г. Воронцов,
А.О. Полапа. Розробка генератора імпульсних
послідовностей для вимірювача частоти.
Виконано
обґрунтування форми імпульсу, відмінної
від прямокутної, при моделюванні сигналів
в телекомунікаційних системах для
урахування виникаючої похибки, що грає
важливу роль при оцінюванні моделей
методів високоточного вимірювання
частоти. Запропоновано використання
такого представлення сигналу для
моделювання вимірювача частоти на
основі раціональних наближень. Розроблені
моделі генератора імпульсних послідовностей
з урахуванням висунутих вимог в таких
програмних пакетах, як SystemView by ELANIX і
MatLab. Проведено порівняльний аналіз і
вибрана найкраща реалізація.
Ключові
слова:
генератор
імпульсних послідовностей, метод
раціональних наближень, моделювання,
SystemView, MatLab, фронт імпульсу.
Воронцов А.Г., Полапа А.А., 2013