Анализ влияния джиттера на быстрые измерения частоты

Oleg Sergiyenko, Daniel Hernбndez Balbuena , Vera Tyrsa , Patricia Luz A. Rosas Mйndez ,

Moises Rivas Lopeza, Wilmar Hernandezd, Mikhail Podrygaloe, Alexander Gurkoe

Источник (англ.): O. Sergiyenko, Analysis of jitter influence in fast frequency measurements/ Oleg Sergiyenko, Daniel Hernаndez Balbuena , Vera Tyrsa et al.// Measurement, Elsevier, vol. 44, no.1, 2011, pp. 1229-1242.

Автор перевода: А.А. Полапа

Реферат

Эта статья представляет собой теоретический анализ возможных последствий влияния джиттера при применении числовых критериев для быстрого измерения частоты на основе принципа совпадения. Основной задачей является генерация сигнала, содержащего известное значение каждого из компонентов суммарного джиттера. Этот сигнал использовался для тестирования сигналов регулярной импульсной последовательности. Первоначально, компоненты джиттера анализировались и моделировались индивидуально. Далее, последовательности для объединения различных видов джиттера моделировались, симулировались и оценивались. Имитационная модель джиттера в Matlab используется, чтобы показать независимость результатов измерения частоты от общего джиттера, который присутствует в эталонной и желаемой последовательности импульсов независимо. Хорошее согласование между представленной ранее теорией быстрого измерения частоты и моделированием с наличием джиттера проверяется; эти результаты позволяют инженерам использовать цифровые критерии для быстрого измерения частоты, несмотря на взаимодействие между компонентами джиттера в различных приложениях для датчиков измерения частоты.

1. Введение

Известно, что множество практических применений (приложений) в различных областях современной электронной техники, как отмечается в [1, с. 136], сильно зависит от точности частотных измерений. Также известно [2], что лучшим способом для правильной оценки частоты является длительное наблюдение сигнала с регистрацией отклонения кривой Аллана. Необходимость использования кривой Аллана вызвана, прежде всего, наличием в любых импульсных последовательностях такого явления, как джиттер. Строгое определение и систематический анализ явления джиттера будут приведены ниже, в разделе 3. Теперь мы просто рассмотрим джиттер, как произвольное смещение электрического импульса от его теоретически определенного положения. Это смещение, как показано в [3, см. рис. 2 на с. 2], влияет на оба параметра импульса: его амплитуду и положение во временной области. Что касается метода измерения частоты, важно также отметить, что обе импульсных последовательности, неизвестная и эталонная, имеют джиттер. Указанные обстоятельства приводят к тому, что совпадения между двумя сериями импульсов, неизвестной и эталонной (см. рис. 1), может быть трудно зарегистрировать посредством существующих электронных устройств. Но в [1] существование такого совпадения является необходимым условием для функционирования данного теоретического метода. В худшем случае, простое совпадение между двумя перекрывающимися во временной области импульсами могут быть пропущены из-за джиттера и собственного времени задержки при вводе-выводе на логическом элементе И. Таким образом, очевидна важность исследования и анализа влияния джиттера на быстрый метод измерения частоты, представленный в [1]. Во-первых, напомним некоторые основные моменты этого теоретического метода.

2. Быстрый метод измерения частоты: краткое описание

В [1] представлено подробное описание метода для быстрого измерения частоты на основе прямого сравнения двух независимых регулярных последовательностей узких

импульсов. В этом методе событием остановки для процесса измерения частоты является числовое условие на количество импульсов, зарегистрированных (отсчитанных) в последовательности неизвестной частоты. Условие остановки измерения не является электронно обнаруживаемым событием, как в других методах, которые применяются в [4-6].

В этом методе, неизвестная частота измеряется путем сравнения ее с известной эталонной частотой. Переходы через нуль обоих синусоидальных сигналов обнаруживаются, и генерируется импульс на каждом переходе из отрицательной области в положительную. Т.о. генерируются две регулярных независимых последовательности узких импульсов с различной частотой.

Последовательности узких импульсов с неизвестной и известной частотой проверяются на совпадение посредством логического элемента И. Генерируется последовательность импульсов совпадений (рис. 1), а также соответствующий импульса в этом последовательности можно использовать как триггер для запуска пары цифровых счетчиков (событие начала).

Каждая из исходных импульсных последовательностей применяется для различных счетчиков и т.о. получаем одно число для исследуемой последовательности и одно число для эталонной последовательности. Измерение нужной частоты может быть получена умножением известной стандартной частоты на соотношение между числом на цифровом счетчике исследуемой последовательности и числом на счетчике эталонной последовательности[1].

Численные значения для неизвестной частоты, полученные вышеописанным способом, маловероятно изменятся со временем для каждого нового процесса счета на цифровых счетчиках, но глобальная сходимость относительной погрешности частот к нулю можно наблюдать при измерениях в течение достаточно длительного времени. Это общее и характерное поведение результатов зависит от соотношения между частотами обоих импульсных последовательностей (или аналогичные соотношения их периодов) и ширины импульсов. В вычислительных экспериментах, в которых контролируются длительность импульсов в каждой последовательности, немонотонная ниспадающая характеристика и переменная сходимости к локальному минимуму неопределенности частоты очевидна, при коротком времени измерения (менее 1 с для данных частот) [1].

Предположение: (а) существование «наибольшего общего измерения (делителя, масштаба?)» между периодами обеих импульсных последовательностей, (б) измерение частоты по совпадению импульсов формулируется как проблема диофантовых приближений, и (с) десятичная система счисления. Числовым условием, которые мы предлагаем, чтобы остановить процесс измерения: значение на счетчике исследуемой частоты (результирующее количество целых периодов в последовательности неизвестной частоты) представлено ​​как 10 ^ r, или 1 последующий за r нулями [1].

Идеальный синхросигнал имеет фиксированный период и скважность, которые никогда не меняются с течением времени и начальной точкой, которая фиксирована во времени. Тем не менее, реальный сигнал содержит небольшие вариации в фазе, периоде и скважности, как правило, называемые джиттером.

В методе измерения частоты эти вариации ключевых моментов влияют на импульсные последовательности известной и неизвестной частот, а также на импульсную последовательность совпадений.

В настоящей работе основной целью является исследование того, какие природные источники фазового шума могут повлиять на процесс измерения, того, как это происходит, и насколько это может повлиять на процесс регистрации наилучшего совпадения.

4. Влияние джиттера на метод измерения частоты

Рассмотрим две последовательности узких импульсов Sx(t) и S0(t) с периодами Тх и T0 соответственно, которые имеют длительность импульса τ. Обе последовательности генерируются при обнаружении переходов через нуль двух синусоидальных сигналов частоты: f0 (стандартная частота) и fx (неизвестная частота). Предположим, что обе импульсных последовательности начинаются в фазе, т.е. сдвиг по времени равен 0. Если обе последовательности поступают на входные портам элемента И, нерегулярная импульсная последовательность формируется из импульсов от частичных и полных совпадений, что показано на рис. 1.

Для измерения частоты, временные интервалы n0T0 и nxTx сравниваются (рис. 1), где n0 - это количество периодов T0 за время измерения, а nx - это количество периодов Тх в тот же промежуток времени. Время измерения может быть определено как временной интервал между первым импульсом совпадения (стартовое событие) после начала процесса измерения и любым другим следующим импульсом совпадения (событие остановки).

Как упоминалось в предыдущем разделе, n0 и nx являются количеством импульсов, полученных на двух независимых цифровых счетчиках.

Математическое условие совпадения импульсов:

где ε является допустимой терпимостью (обоснованным значением ошибки между временными интервалами n0T0 и nxTx) [1,7]. Из уравнения (6), измерение частоты выражается:

А относительная погрешность измерения (смещение [сдвиг] частоты) β может быть выражено

Мы видим в (8), что относительная погрешность измерения ограничивается соотношением между допустимой терпимостью на ошибки сравнения между временными интервалами n0T0 и nxTx и, интервал времени n0T0. Значение n0T0 примерно равно времени измерения (см. рис. 1).

5. Моделирование джиттера импульсных последовательностей

В вычислительных экспериментах момент времени появления каждого импульса в обеих последовательностях узкие импульсов Sx(t) и S0(t) рассчитываются с помощью уравнений:

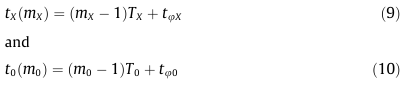
для переднего фронта. Где Tx является гипотетическим значением периода импульсной последовательности с неизвестной частотой, T0 период импульсной последовательности с известной частотой, tφx и tφ0 являются временными интервалами, связанными с начальной фазой каждой импульсной последовательности и, mХ и m0 целые числа, представляющие собой число импульсов в каждой последовательности в окне времени моделирования. Графическая интерпретация этих параметров представлена на рис 4а.

Для каждого импульса в обеих импульсных последовательностях, вариации времени моментов появления переднего фронта рассчитываются и добавляются к моментам времени, полученным по (9) и (10), в зависимости от типа применяемого джиттера, используя

где txj(mx) и t0j(m0) являются моментами времени появления фронтов в каждой импульсной последовательности, содержащей джиттер; tx(mx) и t0(m0) являются моментами времени появления фронтов без джиттера, а Δtx и Δt0 являются их временными сдвигами друг относительно друга (могут принимать как положительные, так и отрицательные значения), при этом они представляются как краткосрочные ненакапливающиеся вариаций. Совпадения между импульсами в последовательностях получены с использованием условий совпадения

где τx и τ0 – значения ширины импульсов каждой из последовательностей узких импульсов.

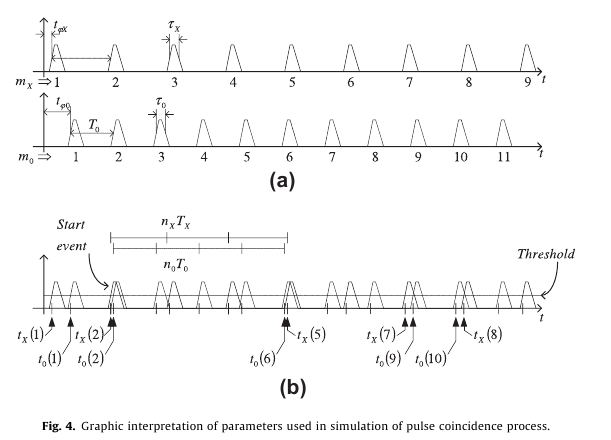
Совпадение импульсов выбрается в качестве «события начала измерения» в вычислительных экспериментах. Используя это совпадение для счета, количество импульсов для следующий совпадений постоянно подсчитывается и, n0 и nx рассчитываются для каждого следующего совпадения.

Для каждого последующего совпадения от выбранного как «событие начала измерения» частота измеряется как

и относительная погрешность измерения с помощью (8).

7. Анализ результатов

Как показали результаты вычислительного эксперимента, состояние наилучшего приближения, полученное в работе [1] инвариантно (независимо) от джиттера. Это заявление является неизменным для любого вида джиттера. Этот основной вклад данного исследования расширяет базис для использования метода реализации быстрого измерения частоты, особенно для различных практических приложений [16,17] для датчиков, чувствительных в частотной области, или повторяющихся процессов измерения с возможностью применения принципа непрерывного совпадения двух независимых шкал (шкала измерения) [18,19].

Только одно обстоятельство может быть критическим из представленных выше: все эти результаты моделирования получены при учете предположений, заявленных в начале главы 3, что временной джиттер имеет некумулятивные изменения. Не существует других предположений о различном поведении джиттера в наиболее фундаментальных ссылках в этой области [7,8,12]. Однако, для полного анализ всех шумовых эффектов при измерении частоты в соответствии с [1], на наш взгляд, желательно исследование возможного накапливающегося теплового дрейфа импульсов в последовательности при изменении температуры. Понятно, что такая задача более соответствует реальным экспериментам, чем компьютерному моделированию. Для этой цели был сделан опытный образец измерительной системы на рис. 9.

Упрощенная функциональная схема частотомера на рис. 9, представлена на рис. 10 [1, с. 139]. Импульсные сигналы с частотами fx и f0 поступают на три элемента И. До первого совпадения на элементе И1, триггер Tr предотвращает активность элементов И2 и И3.

После наступления совпадения, счетчики P и Q проводят подсчет количества импульсов обеих частота до тех пор, пока счетчик P не получит результат в форме. Этот сигнал приводит к активизации обратной связи, которая сбрасывает триггер в исходное состояние. Измерение закончено.

Мы утверждаем, что при окончании измерения, считываемый результат со счетчика является лучшим пропорциональным приближением к истинному значению измеряемой частоты на заданном интервале времени.

Анализ влияния долгосрочного накапливающегося теплового дрейфа импульсов от их идеальных позиций во времени будет предметом наших будущих публикаций.

8. Выводы

Анализируя результаты моделирования возможного практического влияния джиттера на результаты измерения частоты методом, представленным в [1], мы можем объявить следующее.

1)Случайные и детерминированные компоненты джиттера моделируются, и каждая из них влияет по-разному на общее поведение импульсов двух импульсных последовательностей, используемых в методе, и на последовательность, образованную их пересечением во временной области.

2) В этой работе были рассмотрены и представлены посредством компьютерного моделирование четыре различных известных и описанных в современной литературе источника джиттера.

3)Результаты моделирования доказывают инвариантность (независимость) позиции наилучшего приближения относительно любого из описанных в литературе источников краткосрочных некумулятивных вариаций значащих моментов сигнала от их идеальных позиций во временной области.

Благодарности

Конкретные результаты этого исследования, описанные здесь, были доложены на нескольких конгрессах [13-15], мы благодарны организаторам конгрессов за плодотворные обсуждения. Авторы посвящают эту статью в памяти нашего учителя, Dr. Valentin Tyrsa, и хотели бы поблагодарить анонимных рецензентов за ценные комментарии и замечания.