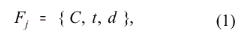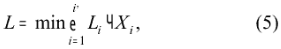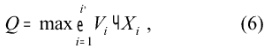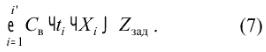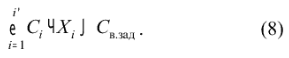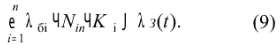Плугина Т.В., Шевченко М.В. - Моделі автоматизованного проектування конвеєрного транспорту підприємства

Аннотация

Плугина Т.В., Шевченко М.В. Моделі автоматизованного проектування конвеєрного транспорту підприємства Розглянуто завдання проектування конвеєрного транспорту підприємства. Розроблено математичні моделі автоматизованого проектування територіально-розподілених конвеєрних ліній. Запропоновано алгоритм оцінки завантаженості лінії і формування керувальних дій.

Аналіз публікацій

Існуюча сучасна апаратура автоматизації конвеєрних ліній, що побудована із застосуванням мікропроцесорної техніки [1], виготовляється в одиничних екземплярах маленькими партіями, що ускладнює організацію ремонтно-профілактичних робіт [2]. Серійні апарати, які вже випускаються для автоматизації конвеєрного транспорту, виконані на дискретних елементах [3]. Застаріла елементна база встановлює межу зростання функціональних можливостей, зокрема за інформацією, засобів автоматизації [4].

На підставі існуючих проблем формулюються мета та задачі дослідження.

Задачі дослідження:

проаналізувати існуючі методи керування конвеєрним транспортом підприємства;
обгрунтувати та розробити математичні моделі;
побудувати алгоритм та функціональну схему керування конвеєрним транспортом.

Мета і постановка задачі

Метою роботи є підвищення ефективності процесу проектування конвеєрних ліній за рахунок відомих та розробки нових моделей, методів, технологій та програмних комплексів проектування таких типів об'єктів.

Приведемо постановку задач дослідження. Відомо:

параметри та робочі характеристики часткових конвеєрних ліній (кількість, енерговитрати, вартість, потужність, інтенсивність відмов складових);
кількість видів локальних бункерів конвеєрної лінії;
параметри та характеристики вантажу.

Необхідно розробити оперативну систему керування територіально розподіленими лініями конвеєрного транспорту залежно від критеріїв і обмежень за максимального коефіцієнта заповнення локальних бункерів та мінімальних енерговитрат.

Математична модель проектування

Особливість цього класу транспортних систем полягає в обміні вантажами між локальними пунктами конвеєрних ділянок через ієрархічну систему функціональних центрів (вантажних терміналів), які виконують функції накопичування вантажів, групування їх за напрямками, комутації виду транспорту (автомобільного, залізничного, авіаційного, водного), вантажної обробки. Методи дослідження територіально розподілених ліній конвеєрного транспорту базуються на методах математичного моделювання й автоматизованого проектування, дискретного програмування, багатокритеріальної оцінки й оптимізації для вибору оптимального режиму керування конвеєрним транспортом.

Цьому питанню було присвячено ряд аналітичних досліджень, в результаті яких сформульовано такі можливі критерії оптимального управління:

мінімальний час простою ділянок унаслідок відмов конвеєрних лінії;
мінімальна витрата електроенергії на транспортування одиниці ваги вантажу;
мінімальний знос матеріальної частини конвеєра на транспортування одиниці ваги вантажу.

Управління за першим критерієм здійснюється за рахунок використання здатності акумулювати вантаж в зоні транспортування і бункерах на лінії, що тимчасово відмовила. Даний критерій реалізується при регулюванні процесу завантаження і вивантаження бункера залежно від кількості вантажу, що знаходиться в даний момент в підбункерній точці М збірного конвеєра КЛМ1 (рис. 1).

Рис. 1. Технологічна схема магістральної конвеєрної лінії

Управління за другим і третім критеріями здійснюється за рахунок скорочення загального часу вільних пробігів і раціонального завантаження конвеєрної стрічки. Скорочення часу вільних пробігів стрічки може реалізуватися регулюванням швидкості стрічки.

Тому як критерій керування доцільно застосовувати критерій «мінімальні енерговитрати», який не суперечить іншим, але більш загальним.

Для даного критерію цільова функція витрати, викликаної зупинкою ділянки, яка містить накопичувальний бункер, лінію до і після бункера, а також місткість на вантажному пункті матиме такий вигляд

де С – вартість матеріалу, одержаного із забою за одиницю часу; t – інтервал часу, протягом якого керуючі дії залишаються незмінними; d – кількість інтервалів усередині будь-якого наперед заданого часу керування; F_j – логічна функція, значення якої визначає можливість технологічного простою ділянки, викликаного транспортом.

При цьому повинні виконуватися обмеження, які визначають моменти пуску і зупинки конвеєрів за відсутності завалів перевантажувальних пристроїв.

У даному випадку математична модель управління системою за обраним критерієм матиме такий вигляд

Часткові критерії

де Z – ефект системи, в загальному випадку це є неспадна функція її вартості; С_в – собівартість здобутого матеріалу; t_i – час роботи окремої ділянки конвеєра; Х_i – дана ділянка.

Мінімальна собівартість матеріалу, здобутого на окремій ділянці

Мінімальна інтенсивність відмов елементів, технічних засобів у блоці

де λ_бі – базове значення інтенсивності відмов елемента і-го виду; N_і – кількість елементів і-го виду в технічному блоці; K_пі – поправочний коефіцієнт для елементів і-го виду; n – кількість видів різнотипних елементів у зборці.

Мінімальна довжина ділянок конвеєрних ліній реалізується за допомогою такого виразу

де L_i – довжина окремої ділянки.

Максимальний вантажопотік, який, у свою чергу, залежить від швидкості роботи конвеєрної стрічки

де V_i – швидкість обертання конвеєрної стрічки на окремій ділянці; X_i – дана ділянка.

На галузь застосування наведених критеріїв накладаються такі обмеження.

Енерговитрати системи не повинні перевищувати заданого значення Z_зад

Собівартість одиниці здобутого матеріалу на окремій ділянці не має перевищувати задану

Необхідне значення інтенсивності відмов елементів не має перевищувати заданого

Протяжність ділянок конвеєрних ліній має перевищувати заданої:

Вантажопотік системи має знаходитися у заданих межах

Система оптимального керування, розроблена за даними моделями, може разом з типовими вимогами реалізувати додаткові вимоги, що залежать від параметрів технологічного процесу:

пуск, зупинка конвеєрної лінії або її частини залежить від завантаження окремих конвеєрів;
завантаження накопичувальних бункерів виконується з контролем рівня маси;
оптимальне вивантаження накопичувальних бункерів здійснюється з попереджаючим контролем завантаження магістрального збірного конвеєра.

На підставі розроблених моделей наведено алгоритм [3] контролю й керування конвеєрними лініями пропонованої системи, де прийняті наступні позначення:

V_пп – об'єм заповнення на вантажному пункті;
Q – інтенсивність повного вантажопотоку в точці М, м³/с;
V₁,...,V_n – об'єми заповнення 1,...,n-го бункерів, м³;
Q₁,...,Q_n – інтенсивність вантажопотоків що поступають відповідно на 1,...,n-ий бункери, м³/с;
q₁,...,q_n – продуктивність 1,...,n-го бункерів, м³/с;
q – інтенсивність вантажопотоку в місці розвантаження збірного магістрального конвеєра;
t_i – час транспортування вантажу від і-го бункера до точки М.

На початку роботи системи задаються значення вхідних параметрів, таких як об'єм на вантажному пункті та об'єми бункерів, інтенсивність повного вантажопотоку та інтенсивність вантажопотоків, що поступають відповідно від окремих бункерів, продуктивність цих бункерів та інтенсивність вантажопотоку в місці розвантаження збірного магістрального конвеєра.

Зміна об'єму окремих бункерів за часом дорівнює інтенсивності вантажопотоку в місці розвантаження збірного магістрального конвеєра.

Далі перевіряється умова зміни об'єму на вантажному пункті. Якщо об'єм стає більшим або рівним об'єму вимкнення на цьому пункті, то система виконує наступні дії: припиняється вантажопотік на накопичувальних бункерах та вимикаються стрічкові конвеєри магістральної конвеєрної лінії

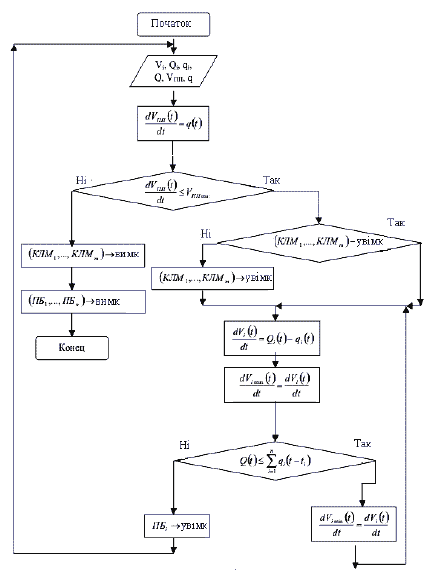
Рис. 2. Алгоритм оцінки полягання завантаженості лінії і формування керуючих дій

Допоки умова є вірною – перевіряється вірність наступної умови щодо увімкнення стрічкових конвеєрів магістральної конвеєрної лінії. Невірність цієї умови визначає увімкнення конвеєрів, про які йшлося вище.

Висновки

Наведені математичні моделі (1) – (11) належать до задач багатокритеріального дискретного програмування з булевими змінними. Для їх реалізації пропонується використати: для задач малої розмірності – метод гілок та меж; для задач великої розмірності – метод випадкового пошуку.

Розроблено модель конвеєрної лінії, що одночасно враховує паралельний масив критеріїв із п чисел та порівнює поточні результати із зовнішнім порогом. Це забезпечує максимальний паралелізм та прискорення обробки масиву чисел, оскільки у випадку перевищення суми над порогом цей факт можна зафіксувати без формування остаточного значення суми всіх чисел масиву.

Розроблені математичні моделі та запропонований алгоритм, на відміну від існуючих, допомагають вибрати ефективну систему керування залежно від функціонального призначення проектованого конвеєрного транспорту за заданими критеріями й обмеженням.

Список использованной литературы

1. Коновалова И.П., Мелькумов Л.Г., Ротенгберг В.М., Травкин Е.К. Алгоритмы оптимального управления подземными конвейерными линиями // Оперативно-диспетчерское управление и АСУ ТП на угольных предприятиях. - Труды института. Гипроуглеавтоматизация. – М„ 1980. – с. 16-26.
2. Бурлаков М.В. Об автоматизации управления дискретными технологическими и информационными процессами // УСиМ. – 1996. – № 4/5. – с. 57-67.
3. Петров Е.Г., Новожилова М.В., Гребеннік Ш.В. Методи і засоби прийняття рішень у соціально-економічних системах: Навч. посібник. – Харків: ХДТУБА, 2002. – 284 с.
4. Справочник по автоматизации шахтного конвейерного транспорта / Н.И. Стадник, В.Г. Ильюшенко, С.И. Егоров и др. – К.: Техника, 1992. – 438 с.