
При моделировании динамических процессов в рабочем органе конвейера, математическая модель может быть представлена в виде совокупности упруго-связанных звеньев (2), где x0, xk, xN, v0, vk, vN - координата и скорость движения первого, k-ого и последнего звена соответственно, L0 – длина элементарного звена, kу - коэффициент упругости (жесткости) элементарного звена.
В состав каждого звена входят цепь, скребок, груз. На каждое звено массой и длиной L0 действуют силы со стороны соседних звеньев 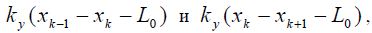 силы внешнего (сухого) трения
силы внешнего (сухого) трения  , зависящие от скорости движения звена
, зависящие от скорости движения звена 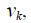 , а также тангенциальная составляющая силы тяготения
, а также тангенциальная составляющая силы тяготения 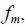 , величина которой определяется положением конвейера.
, величина которой определяется положением конвейера.
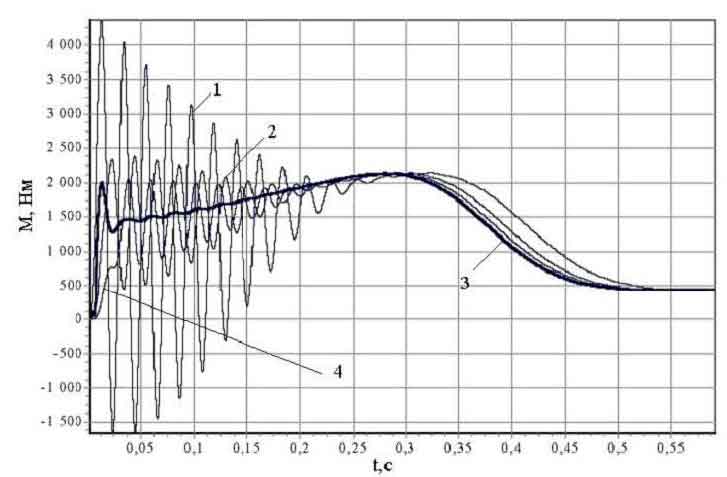
Рис 2. Переходные моменты при прямом пуске (1), при пофазной подаче напряжения (2), при квазиоптимальном пуске (3), при пуске ограничением скорости нарастания приложенного напряжения.
Усилие, передаваемое со стороны приводного двигателя 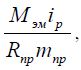 задаётся через начальную координату системы. Здесь
задаётся через начальную координату системы. Здесь 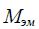 – электромагнитный момент электродвигателя,
– электромагнитный момент электродвигателя, 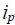 – передаточное отношение редуктора,
– передаточное отношение редуктора, 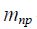 – приведенная масса вращающихся частей привода,
– приведенная масса вращающихся частей привода,  – радиус приведения.
– радиус приведения.
На последнее звено 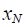 системы действует усилие только со стороны предпоследнего звена, так как при наличии в составе конвейера одной приводной станции обратная ветвь тяговой цепи будет провисать. Это отражено в представленных уравнениях.
системы действует усилие только со стороны предпоследнего звена, так как при наличии в составе конвейера одной приводной станции обратная ветвь тяговой цепи будет провисать. Это отражено в представленных уравнениях.
Правомерность подобного подхода для описания движения рабочего органа скребкового конвейера обоснована в [3]. При корректном задании значений коэффициентов перед переменными в приведённой модели, результаты моделирования достаточно хорошо согласуются с результатами экспериментов.
На рис.1 представлены расчетные графики изменения момента, частоты вращения ротора и тока в обмотках статора и ротора при прямом пуске конвейера, полученные при компьютерном моделировании. Использовались следующие параметры: длина конвейера – 100 м, калибр цепи – 18 64, масса одного метра цепи со скребками – 18 кг, масса груза - 10 кг/м, передаточное отношение редуктора ip – 20, рабочий орган приводится в движение асинхронным электродвигателем ЭД-КО4-4МУ5 мощностью 80 кВт.
Как видно из рис. 1, приводной электродвигатель развивает значительные по величине знакопеременные электромагнитные моменты, приводящие к опасным механическим напряжениям в трансмиссии и тяговой цепи конвейера. При этом пусковые токи в обмотках электродвигателя достигают величин, в несколько раз превосходящих номинальные значения, что негативным образом сказывается состоянии лобовых частей статорной обмотки.
На рис. 2 приведены переходные моменты при моделировании пуска АД с резкопеременной нагрузкой различными способами. Наилучшие свойства реализации безударного пуска получены при квазиоптимальном управлении [4]. Экспериментальная проверка с помощью разработанного нам универсального полупроводникового пускового устройства подтвердила полученные при моделировании результаты.
Перечень ссылок
1. Ещин Е.К. Теория предельных режимов работы горных машин, Томск: Изд-во Томского ун-та, 1995. – 232 с.
2. Моделирование асинхронных электроприводов с тиристорным управлением / Л.П. Петров, В.А. Ладензон, Р.Г. Подзолов, А.В. Яковлев. – М.: Энергия, 1977. – 200 с.
3. Бандурин А.Н. Моделирование динамики рабочего органа скребкового конвейера //Вестн. КузГТУ. –1999. – №2. – С.46-49.
4. Патент РФ № 2235410 МПК Н 02 Р 1/26. Способ пуска асинхронного электродвигателя / Е.К. Ещин, И.А. Соколов, В.Л. Иванов, В.Г. Каширских, Заявл. 04.01.03, № 2003100098. Опубл. 27.08.04. Бюл. №24.
 фазные токи и напряжения;
фазные токи и напряжения; 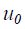 – разность потенциалов между нулевыми точками звезды напряжений сети и звезды напряжений электродвигателя;
– разность потенциалов между нулевыми точками звезды напряжений сети и звезды напряжений электродвигателя;  – взаимная индуктивность обмоток статора и ротора;
– взаимная индуктивность обмоток статора и ротора; 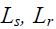 – индуктивности статора и ротора;
– индуктивности статора и ротора; 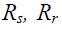 – активные сопротивления статора и ротора;
– активные сопротивления статора и ротора; 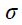 – коэффициент рассеяния;
– коэффициент рассеяния;  – соответственно составляющие потокосцепления обмотоки ротора и токов статора по осям неподвижным относительно статора;
– соответственно составляющие потокосцепления обмотоки ротора и токов статора по осям неподвижным относительно статора; 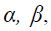 – число пар полюсов;
– число пар полюсов;  – частота вращения ротора и электромагнитный момент.
– частота вращения ротора и электромагнитный момент.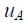 необхомо подать напряжение равное
необхомо подать напряжение равное  при этом
при этом 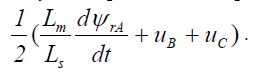
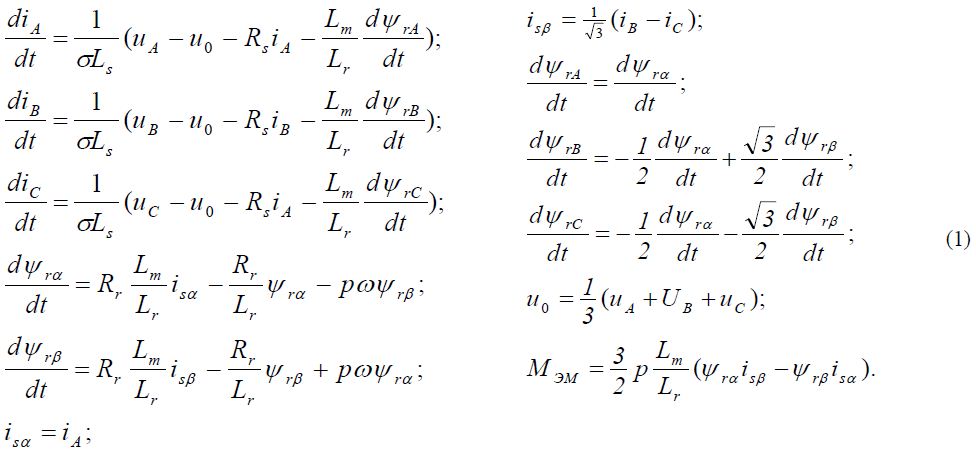

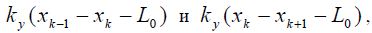 силы внешнего (сухого) трения
силы внешнего (сухого) трения  , зависящие от скорости движения звена
, зависящие от скорости движения звена 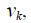 , а также тангенциальная составляющая силы тяготения
, а также тангенциальная составляющая силы тяготения 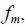 , величина которой определяется положением конвейера.
, величина которой определяется положением конвейера.
 и тока в обмотках статора
и тока в обмотках статора  и ротора
и ротора  при прямом пуске
при прямом пуске
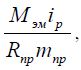 задаётся через начальную координату системы. Здесь
задаётся через начальную координату системы. Здесь 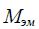 – электромагнитный момент электродвигателя,
– электромагнитный момент электродвигателя, 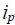 – передаточное отношение редуктора,
– передаточное отношение редуктора, 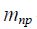 – приведенная масса вращающихся частей привода,
– приведенная масса вращающихся частей привода,  – радиус приведения.
– радиус приведения.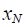 системы действует усилие только со стороны предпоследнего звена, так как при наличии в составе конвейера одной приводной станции обратная ветвь тяговой цепи будет провисать. Это отражено в представленных уравнениях.
системы действует усилие только со стороны предпоследнего звена, так как при наличии в составе конвейера одной приводной станции обратная ветвь тяговой цепи будет провисать. Это отражено в представленных уравнениях.