Вячеслав Ловейкин, Ольга Костина – Оптимизация способа запуска скребка конвейера

Аннотация

Статья посвящена методам оптимизации способа запуска скребка конвейера. Критерий, который отобран, чтобы оценить способ движения конвейера, является среднеквадратичным отклонением ускорения цени конвейера и центра масс скребков с цепью и грузом. Получено оптимальный способ движения системы и закон изменения ведущею момента, который приводит динамическую нагрузку к минимуму.

Ключевые слова:

скребок конвейера, математическая модель, динамическая нагрузка, оптимальный способ движения, отличительное уравнение движения.

Введение

Предыдущими теоретическими исследованиями [8, 9] мы определили, что в цепи конвейера скребка возникают колебательные процессы со значительным изменением скорости и ускорения во время запуска. Такие процессы были вызваны динамическим нагрузками в цепи конвейера и элементах диска. Все они приводят к преждевременному разрушению и уменьшению надежности работы конвейера.

Чтобы решить такую проблему, необходимо минимизировать динамические нагрузки посредством выбора оптимального закона движения скребка конвейера во время запуска. Чтобы оптимизировать управление трафиком часто используют вариационное исчисление, которое дает шанс получить гладкие операционные функции. Это позволяет «смягчать» режим движения системы.

Материал и методы

Работа [10] посвящена, исследованию оптимизации режимов движения различных механических систем.

В данной статье [12] описан метод для решения проблемы оптимизации движения механических систем, используя прямой метод изменения. Авторы минимизировали среднеквадратичное значение динамического компонента движущих сил механической системы.

В работе [11] рассматривают путь к устранению колебания груза во время запуска краба подъемного крана. Поскольку критерий оптимизации переходного режима принят квадратичное различие скорости краба подъемного крана и груза.

Работы [7] [15, 16] имеют дело с конструкцией математических моделей и исследованием динамических процессов, которые возникают в конвейерах с цепью.

Исследование [7] посвящено математической модели для определения нагрузок в управлении механизмом и цепью конвейера скребка с асинхронными электродвигателями с двумя высокими скоростями на примере угольной транспортировки.

Однако, исследование режимов движения оптимизации конвейеров скребка для транспортировки сельскохозяйственных грузов фактически не было выполнено.

Поэтому цель исследования – режим запуска оптимизации конвейера скребка для минимизации динамических загрузок, которые возникают в цепи и управляют элементами конвейера.

Результаты и обслуживание

Оптимизация процесса запуска выполнена с использованием динамической модели с четырьмя массами конвейера скребка (рис. 1). Нерабочее ответвление конвейера не принято во внимание, потому что от предыдущих исследований мы имеем установленный, незначительно влияющий характер движения.

Рис. 1. Динамическая модель скребка конвейера

Создавая математическую модель, мы сделали такие предположения:

Все элементы конвейера скребка абсолютно крепкие тела, кроме элементов механизма передачи и цепи, которые имеют эластичные свойства.
Тело управления механизмом конвейера и отношениями валов цепного колеса тяги и цепного колеса силы фиксировано абсолютно твердо.

Набор дифференциальных уравнений, который описывает динамические процессы в конвейере скребка, сделан на основе принятой динамической модели с использованием принципа Даламбера и выглядит так:

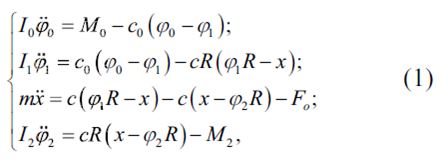
где

I0 – момент инерции элементов управления механизмом, которые установлены к оси из вала питания;

I1, I2 – моменты инерции управления вала и вала силы конвейера, касающиеся собственной оси вращения;

– угловые координаты поворота соответственно управления механизмом, управления цепного колеса и цепного колеса силы конвейера;

x – линейная координата центра масс рабочего ответвление конвейера;

m – масса, которая сконцентрирована на рабочее ответвление конвейера;

c0 – коэффициент жесткости управления механизмом, который установлен к поворачивающейся оси из вала питания;

с – коэффициент жесткости тяги цепи конвейера;

R – радиусы ведущего цепного колеса и цепного колеса силы;

M0 – вращающий момент запуска на вале двигателя, который установлен к поворачивающейся оси питания вала;

M2 – момент сопротивления, являющегося результатом выкапывание груза скребками, который установлен к поворачивающейся оси вала силы;

F – сила сопротивления от перемещения рабочего ответвления конвейера.

От уравнений системы (1) мы находим линейную координату центра масс рабочего ответвления конвейера x, угловые координаты поворота управления механизмом , управление барабаном , и также начальный вращающийся момент M0, используя угловую координату 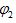и производные. При этом момент управления имеет вид:

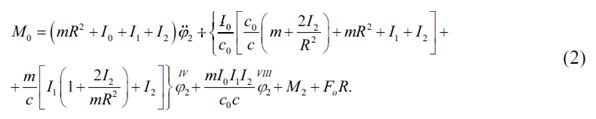
Интегральные функционалы используются в качестве критериев к оценке режимов движения машин. Они зависят от режимов движения механизмов. Функционалы выводят на экран динамику машин взятую во внимание созданной математической модели [12]. Поскольку эти критерии выводят на экран нежелательные свойства механизмов, они должны быть минимизированы.

Критерий оценки режима движения скребкового конвейера во время запуска среднеквадратичное отклонение от ускорений цепи в течении момента работы управления барабаном и центра массы скребка с цепью и грузом. Принятое во внимание уравнение системы (1), критерий имеет вид:

где t1 – время ускорения конвейера;

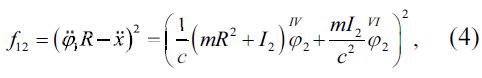
Уравнение Юлер-Пуэссона [2] является минимальным условием критерия (3) с подинтегральным выражением (4)

Так как функция f12 зависит от 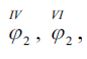; уравнение (5) принимает следующий вид:

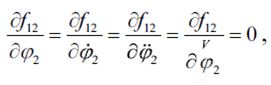
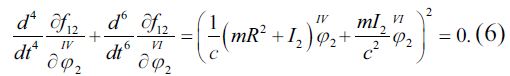
Чтобы упростить решение, принимаем такие обозначения:

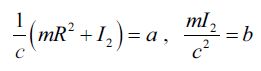
Определив частные производные и производные времени для уравнения (6), мы имеем полученный результат:

Мы определили общее решение уравнения (7). С этой целью мы нашли корни характерного уравнения. Полагая, что 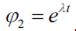, мы запишем уравнение (7) так:

где 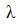– корень характеристики уравнения.

Так как

В результате выполняемых вычислений для конвейера с параметрами

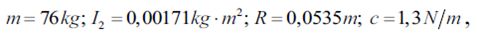
мы нашли корни характеристического уравнения:

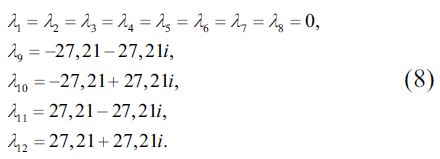
Поскольку мы имеем восьмикратне выраженные и сложные корни характеристического уравнения (8) решение дифференциального уравнения (7) выглядит как:

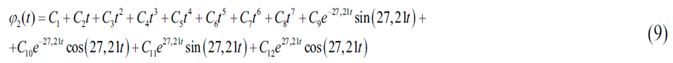
где 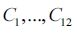– постоянные интегрирования, которые определяются из начальных условий движения.

Для определения этих констант это необходимо установить двенадцать граничных условий движения:

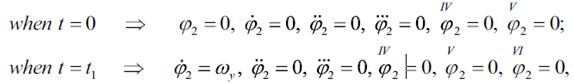
где 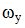– обосновывающаяся скорость поворота вала силы.

Определив константы интеграции, мы подставили их в выражение (9) и получили оптимальный закон движения силы барабана.

Посредством этого режима, используя уравнение из системы (1), оптимальные режимы движения управление механизмом и управление барабаном конвейера получены. Изменение скорости и ускорения этих связей имеет тот же характер что и в барабане силы.

Графики угловой скорости (рис. 2), углового ускорения (рис. 4) вала силы в оптимальном режиме запуска и пуска вращающего момента (рис. 6) получены, использованием следующих параметров динамической модели:

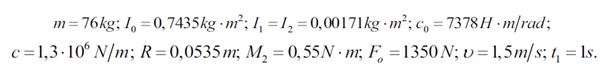
Для того чтобы продемонстрировать влияние оптимизации режима движения конвейера на характеристике движения линии связи конвейеров, мы демонстрируем для сравнения графики изменения угловой скорости и ускорения во время неоптимального (допустимого) режима движения. Графики получены при использовании тех же параметров динамической модели (рис. 3, 5).

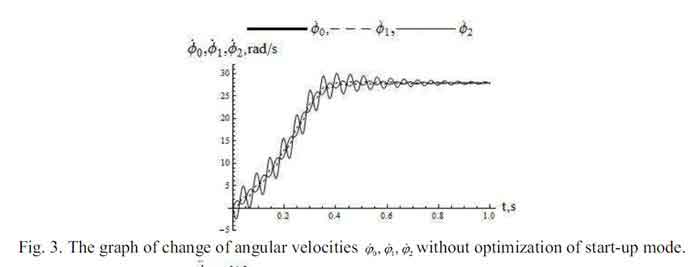
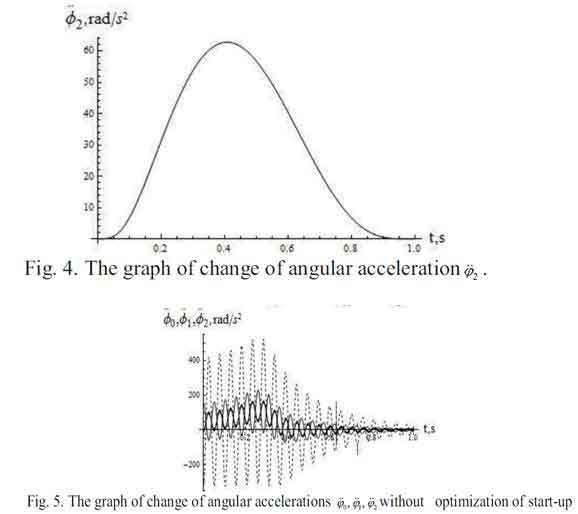
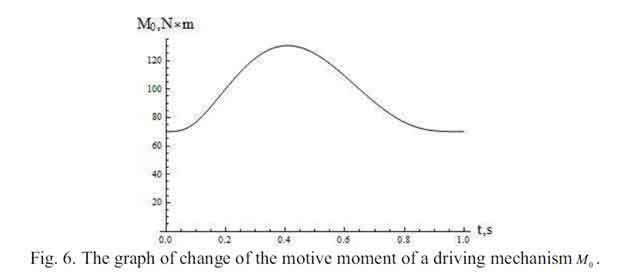
Анализ проводимых исследований и сравнение оптимальных графиков изменения угловой скорости и углового ускорения связи конвейеров к графикам без оптимизации, можно сделать вывод что такой режим запуска дал шанс минимизировать колебания в ссылках диска механизм и гибкой цепи скребкового конвейера, вызываемые динамическими загрузками. Во время допустимого режима движения конвейера колебания угловой скорости были в 10... 6 рад/с, и колебания углового ускорения имели очень интенсивный характер (максимальные значения, измененные от – 250 – 450 рад/с2).

Следовательно, полученный оптимальный режим запуска обеспечивает гладкое изменение угловой скорости и ускорения скребковых конвейеров, а также вращающего момента запуска на валу механизма, установленного к питанию вала конвейера.

Заключение

Была проведена оптимизация динамики движения конвейера при запуске на базе созданной математической модели . Критерий оптимизации среднеквадратичного отклонения цепи ускорения в течение момента работы управления барабаном и массами центра скребка с цепью и грузом. На практике метод оптимизации запуска режим скребкового конвейера может быть уменьшен действием динамических нагрузок к минимуму и, как последствие, повышением производительности и надежности работы конвейера.

Перечень ссылок

1. Астанін В.В. Дінаміка та міцність машин у прикладах i задачах JA стан in В. В., Бородачов М.М., Савченко M.I. – К. : НАУ, 2008. – 184с.

2. Варіаційне числення та методи оптимизації / [Перестюк М.О.. Станжицький О.М., Капустян О.В., Ловейкін Ю. В.]. – К., 2010.– 121с.

3. Виноградов А., Сибирцев А., Журавлев С. Бездатчиковый электропривод подъёмно-транспортных механизмов// Силовая электроника. – №1. – С. 74–84.

4.Гелетій В.М. Комп'ютерне моделювання i визначення фактичних навантажень довгомірних металоконструкцій з гнучкими елементами / В.М. Гелетій // Динаміка, міцність та проектування машин i приладів №6 14. – JI. : Вид-во Нац. ун-ту "Львів. иолггехшка", 2008. –С. 60–62.

5. Дівеєв Б.М. Раціональне моделювання динамічних процесів у складних конструкціях / Б.М. Дівеєв // Автоматизація виробничих процесів у машинобудуванні та приладобудуванні – JI. : Вид-во Нац. ун-ту "Львів. політехніка", 2007.–С. 103–108.

6. Кідрацький Б.І. Динаміка приводу з пружно-запобіжною муфтою у перехідних режимах роботи / Б.І. Кідрацький. А.С. Бурковський // Оптимізація виробиичих процесів i технологічний контроль у машинобудуванні та приладобудуванні. 2008. –№613. –С. 115–126.

7. Кондрахин В.П., Мельник А.А. Математическая модель для исследования нагрузок в двухскоростном многодвигательном приводе и тяговом органе скребкового забойного конвейера / В.П. Кондрахин, А.А. Мельник // Наукові праці ДонНТУ. – 2008. – Вип. 16 (142), Серія: гірнично-електромеханічна. – Донецьк. –С. 132–140.

8. Костина О.Ю. Математична модель динаміки руху скребкового конвеєра / О. Костина, В. Ловейкін // Сільськогосподарські машини: Зб. наук. ст. – Луцьк. 2011. – Т. 1. Вип. 21.– С. 200 – 209.

9. Ловейкін B.C. Дослідження динаміки пуску скребковою конвеєра зі змінним навантаженням в процессі пуску/ В. Ловейкін, О. Костина // MOTROL. – Lublin, 2011. 13В. –С. 42–48.

10. Ловейкін B.C. Оптимізація конструкцій технічних систем Ловейкін B.C., Човнюк Ю.В., Шимко Л.С. – Ніжин: Видавець П.П. Лисенко М.М.. 2010. – 320 с.

11. Ловейкін B.C. Оптимізація перехідних режимів руху кранового візка за інтегральним критерієм квадрату різниці швидкостей візка i вантажу / В .С.Ловейкін, Ю. О. Ромаеевич // Вісник Дніпропетровського державного аграрного університету. – 2010. № 2. – С. 51–55.

12. Ловейкін B.C. Оптимізація перехідних режимів руху механічних систем прямим варіаціонним методом / Ловейкін В. C., Ловейкін А.В., Ромасевич Ю.О. // Вісник ТДТУ. – 2010. – Том 15. – № 1. – С. 7 – 13. –(мехініка та матеріалознавство).