Дослідження роботи противоперевантажних алгоритмів протоколу ТСР при перевантаженнях в каналах зв'язку

Анотація

Трикоз В.В. , Батир С.С. Дослідження роботи противоперевантажних алгоритмів протоколу ТСР при перевантаженнях в каналах зв'язку. Виконані дослідження, моделювання та аналіз роботи алгоритмів для боротьби з переван-таженням протоколів транспортного рівня стека TCP/IP. Для дослідження обрані алго-ритми TCP Reno та TCP Vegas. Розглядані принципи роботи обраних алгоритмів. Для моде-лювання використана гідродинамічна модель потоку, за допомогою якою були враховані особливості роботи обраних алгоритмів. Отримані результати моделювання дозволили оці-нити поведінку алгоритмів при перевантаженнях та ефективність використання пропуск-ної спроможності каналу зв’язку.

Ключові слова:

перевантаження, алгоритм управління перевантаженням, TCP Reno, TCP Vegas, гідродинамічна модель.

Загальна постановка проблеми.

Проблема перевантаження в мережах TСР/ІР виникає у разі, коли кількість переданих даних починає наближатися до значення допустимої пропускної спроможності мережі. При цьому погіршуються основні показники якості обслуговування. Ці погіршення можуть виражатися в збільшенні числа втрачених пакетів і часу затримок. Управління перевантаженнями є актуальним завданням, оскільки кількість кінцевих користувачів глобальної мережі, а, отже, об'єми переданих даних, постійно збільшуються.

Зростає також доля мультимедійного трафіку реального часу, вплив перевантажень на який особливо критично. Завдання механізмів управління перевантаженнями полягає в тому, щоб підтримувати кількість даних, переданих по мережі, нижче за рівень, при якому пропускна спроможність мережі починає різко падати, обмежуючи потоки вхідного і вихід-ного трафіку.

Аналіз існуючих досліджень та публікацій

Перевантаження в каналах зв’язку мереж TСР/ІР є досить давньою, але дуже актуаль-ною навіть сьогодні, проблемою. Їй присвячена велика кількість робіт [1, 2,7,8,9].

Дослідження роботи противоперевантажних алгоритмів транспортного рівня стеку TСР/ІР описано в роботах [3 - 5, 10].

Оскільки для спостерігання поведінки алгоритмів для боротьби з перевантаженням необхідно використовувати таку математичну модель, яка буде враховувати всі особливості роботи алгоритму, то на даний час дуже розповсюдженою є гідродинамічна модель потоку (fluid flow model), яка наведена в роботі [6].

Постановка задач дослідження.

Для дослідження роботи алгоритмів для при для боротьби з перевантаженнями необхідно вирішити наступні задачі:

1. Проаналізувати основні алгоритми, які використовуються в протоколі ТСР для боротьби с перевантаженнями.

2. Розробити реалізацію математичної гідродинамічної моделі для обраних противоперевантажних алгоритмів та провести моделювання роботи цих алгоритмів при різних вхідних параметрах.

3. На основі отриманих результатів провести аналіз та порівняти роботу різних алго-ритмів у однакових умовах.

Вирешення задач та результати дослідження

На даний момент існує цілий ряд реалізацій методів управління перевантаженнями в протоколі TCP, що розрізняються в застосовності до вирішень різних завдань. Наприклад, TCP Vegas дозволяє враховувати стан каналу зв'язки, TCP Westwood враховує високий рівень втрат в каналах зв'язку, TCP Hamilton використовується для локальних мереж з високою пропускною спроможністю. Найбільш розповсюдженими реалізаціями протоколу є TCP Reno та TCP Vegas, які будемо використовувати для подальшого дослідження роботи противоперевантажних алгоритмів.

Проведемо аналіз роботи обраних алгоритмів.

В TCP Reno у нормальної ситуації розмір вікна змінюється циклічно. Розмір вікна збі-льшується під час кожного циклу до втрати пакету. Коли відбудеться втрата пакету, TCP Reno зменшує розмір вікна до половини поточного розміру. Це називається адитивне збіль-шення та мультиплікативне зменшення.

TCP Reno має два етапи зміни розміру вікна:

1) фаза повільного старту

2) фаза уникнення перевантаження

Коли відправник отримує підтвердження доставки в момент часу t + tA [с] поточне значення розмір вікна перевантаження cwnd(t) перетворюється на cwnd(t + tA) відповідно (1):

де ssth(t) [пакет] – значення порогу, при якому TCP йде від фази повільного старту в фазу уникнення перевантаження .

Коли внаслідок таймаута виявлено втрати пакетів, значення cwnd(t) і ssth(t) оновлюються наступним чином:

З іншого боку, коли TCP виявляє втрати пакетів згідно алгоритму швидкої передачі, cwnd(t) і ssth(t) оновлюються іншим чином:

TCP Reno потім переходить у фазі швидкого відновлення. На цьому етапі розмір вікна збільшується на один пакет, коли отримується дублююче підтвердження. З іншого боку, cwnd(t) дорівнює ssth(t) при надходженні підтвердження на пакет, що надіслане знову.

У разі таймаута cwnd(t) ssth(t) приймають вигляд (2).

Як можна легко побачити, механізм уникнення перевантажень, прийнятий в TCP Reno, викликає періодичні коливання через постійне оновлення розміру вікна. Швидкість, з якою кожне з’єднання оновлює розмір вікна залежить від циклу затримки з'єднання. Отже з’єднання із коротшим затримки може оновити розмір вікна швидше, ніж з’єднання з біль-шим часом затримки і тим самим несправедливо вкрасти частку пропускної здатності.

TCP Vegas використовує різницю між очікуваною та фактичною швидкістю потоків для оцінки пропускної здатності мережі. Ідея в тому, що коли мережі не перевантажена, фактична швидкість потоку буде близький до очікуваної. В іншому випадку фактична швидкість потоку буде менше, ніж очікувана швидкість потоку. TCP Vegas за допомогою цієї різниці швидкостей потоку, оцінює рівень заторів у мережі та відповідним чином оновлює розмір вікна. Звернімо увагу, що ця різниці швидкостей потоку можуть бути легко перекладений на різницю між розмір вікна і кількістю визнаних пакетів у часі, використовуючи рівняння:

де Expected - очікувана швидкість, Actual - фактичний швидкість, BaseRTT - мінімальний час проходження сигналу туди та назад при першому з’єднанні.

Деталі алгоритму: 1. Джерело обчислює очікувану швидкість потоку за формулою

де CWND - поточний розмір вікна.

2. Джерело оцінює поточну швидкість потоку за допомогою фактичного часу про-ходження сигналу туди та назад:

де RTT є фактичним часом проходження сигналу туди та назад.

Джерело, використовуючи очікувану та фактичну швидкість потоку, обчислює оцінку відставання у черзі за формулою (4)

Джерело оновлює розмір вікон таким чином:

Рис. 1 ілюструє поведінку. Розглянемо просту мережу з одним підключенням і одним каналом ємністю . Нехай BaseRTT бути затримка мінімального проходження сигналу туди і назад. Пропускна здатність цього з'єднання є window/( BaseRTT) коли window

На рис. 1, w відповідає розміру вікна де window=C * BaseRTT. Коли window> w, починає будуватися черга і (Expected - Actual)> 0. TCP Vegas збільшує розмір вікна під час наступного проходження сигналу якщо window< w+а , зменшується розмір вікна, якщо window> w+б. В іншому випадку, він залишає розміру вікна без зміни.

На рис. 1, Diff оцінює розмір черги. TCP Vegas намагається тримати прийняті а пакети, але не більше, ніж б пакетів в черзі. Причиною цього є що TCP Vegas спробує виявити і використовувати додаткову пропускну здатність, коли вона стає доступна без перевантажень в мережі. Таким чином, коли є тільки одне підключення, розмір вікна TCP Vegas сходиться до точки, що лежить між w +а і w +б.

Звернімо увагу, що цей механізм принципово відрізняється від того, що використову-ються TCP Reno. TCP Reno завжди оновлює розмір вікна, щоб гарантувати повною утиліза-цію пропускної спроможності, що веде до постійної втрати пакетів, тоді як TCP Vegas викликає будь-яких коливання в розмірі вікна після того, як він сходиться до точка рівноваги.

Для дослідження роботи противоперевантажних алгоритмів скористаємося найпростішою моделлю мультісервісной мережі – моделлю з одним вузьким місцем. Для даної топології моделі мережі властиві всі характерні особливості телекомунікаційного трафіку інтегрованої мережі з комутацією пакетів, у тому числі його самоподобність і масштабна інваріантність.

На рис.2 наведена топологія такої мережі. За допомогою s1, s2,…,sN - позначені відправники трафіку, r1, r2, …, rN – одержувачі, R – маршрутизатори каналу. Вузьке місце приводить к тому, що пропускна спроможність всієї мережі обмежена одним або кількома компонентами, які називаються критичними елементами. В нашому випадку, критичними елементами є маршрутизатори каналу.

Розрахунок зміни розміру вікна та довжини черги виконується за допомогою гідродинамічної моделі потоку. Для кожного алгоритму розробляється своя гідродинамічної моделі, яка враховує конкретні особливості даного алгоритму. В даному випадку використовується алгоритми TCP Reno та TCP Vegas .

Гідродинамічна модель потоку включає такі поєднанні нелінійних диференціальних рівнянь з затримкою, яка змінюється з часом:

де W(t) позначає середній розмір вікна TCP [пакети], Q(t) – середня довжина черги [пакети], R(t) – RTT [секунди], С – пропускна спроможність каналу [пакет/с], N(t) – кількість TCP сесій, p(t) – ймовірнісна функція маркірування пакету, G(x) – нелінійна функція, яка описує зміну розміру вікна.

Функція G(x) описується виразом:

Диференціальні рівняння (3) та (4) описують динамічне керування вікна TCP. Перший елемент описує у вікні адитивне збільшення фази, другий елемент – мультиплікативне зменшення фази (в тому числі ймовірнісна функція маркірування пакету). Елемент в рівнянні (9) описує збільшення розміру вікна на 1, а другий елемент – зменшення розміру вікна на 1.

Рівняння (10) описує довжину черги вузьким місцем, як різниця між швидкістю при-буття пакету і пропускною спроможністю С, припускаючи, що там є немає внутрішньої динаміки в вузькому місці (грубо кажучи, простих інтеграторів).

За допомогою гідродинамічної моделі потоку активне керування чергою можна інтер-претувати як зворотній зв'язок проблеми контролю, де дія контролю складається з маркування пакетів (з ймовірністю p) в залежності від довжини виміряної черги Q.

Для кращого розуміння принципу моделі гідродинамічного потоку представимо рів-няння (8) та (10) схемою, яка приведена на рис. 3

Принцип гідродинамічної моделі потоку для TCP Vegas наведено на рис. 4.

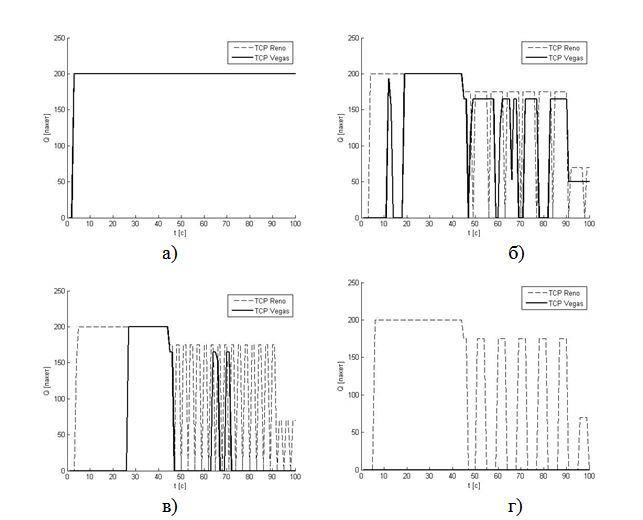
Для моделювання використовуємо пакет прикладних програм MATLAB.

Вхідні параметри моделювання: RTT R=0,1 с, максимальна довжина черги Qmax=200 пакетів, кількість відправників S змінюється динамічно.

Результати моделювання приведені на рис.5-6 та в табл.1.

Як можна побачити з рис. 5 процес формування черги при пропускній спроможності С=1 Мбіт/с ідентичний – за короткий проміжок часу черга достигає свого максимального значення ти не змінюється не дивлячись на зміну кількості користувачів. При збільшенні пропускної спроможності каналу зв’язку спостерігаються відмінності в процесі формування черги при використанні різних алгоритмів. Це ще раз доводить, що алгоритм TCP Vegas ви-користовує пропускну спроможність каналу зв’язку більш ефективно.

Проаналізувавши графіки, приведені на рис.6, можна побачити, що середній розмір вікна TCP Vegas менше ніж у TCP Reno, але за рахунок меншого коливання, TCP Vegas передає більшу кількість даних.

Таблиця 1 - Результати моделювання

	С, [Mbit/с]	V, [пакет]	Vlost, [пакет]	р	Qср,[пакет]
Vegas	1	110707	58	0,0005	198
	10	215395	21	0,00009	143
	50	756532	15	0,00002	37
	100	3632607	0	0	0
Reno	1	101648	58	0,0006	198
	10	203934	43	0,0002	159
	50	730570	36	0,00005	143
	100	3366720	6	0,000003	120

Як можна побачити з табл.1, канал зв’язку з використанням алгоритму TCP Vegas з пропускною спроможністю від 10 Мбіт/с можна вважати каналом високої якості та викорис-товувати для передачі трафіку даних, для якого імовірність втрати пакету повинна бути не більше 10^-4. В той час коли канал зв’язку с використанням алгоритму TCP Reno, набуває та-кого рівня якості при пропускній спроможності від 50 Мбіт/с.

Висновки

1. Моделювання роботи алгоритмів протоколів TCP Reno та TCP Vegas показало що двохфазна робота першого алгоритму призводить до значних коливань навантаження на мережу та більшому рівню втрат, ніж у алгоритму TCP Vegas. За рахунок реалізації більш складної схеми управління пропускною спроможністю, досягнуто зменшення рівня коливань корисного навантаження на мережу та зменшення втрат.

2. Використання гідродинамічна модель потоку дозволяє враховувати особливості функціонування проти перевантажних алгоритмів. Модель може бути використана для мо-делювання поведінки різних реалізацій алгоритму TCP в умовах мереж складеної топології.

3. Проведене моделювання показує, що алгоритм TCP Vegas більш ефективно використовує пропускну спроможність каналу зв’язку, ніж TCP Reno за рахунок меншого коливання розміру вікна.

Перелік посилань

1. Е.А. Кучерявый Управление трафиком и качество обслуживания в сети Интернет - СПб.: Наука и техника, 2004. – 336 с.
2. Джамалипур А. Беспроводной мобильный Интернет. Архитектура, протоколы и сервисы; [пер.с англ. Ш. Салиев, В. Орлов] – М., Техносфера, 2009 – 496 с.
3. Fall K., Floyd S. Simulation based comparisons of Tahoe, Reno and SACK TCP // Computer Communications Review, 26(3):5-21, July 1996.
4. Analysis and comparison of TCP Reno and Vegas [Електронний ресурс] /Jeonghoon Mo, Richard J. La, Venkat Anantharam, and Jean Walrand - режим доступу до статті: http://www.eecs.berkeley.edu/~ananth/1999-2001/Richard/MoLaInfocom1999.pdf
5. Thomas Bonald Comparison of TCP Reno and TCP Vegasvia Fluid Approximation [Електронний ресурс]// RR3563, Unite de recherche INRIA Sophia Antipolis Cedex (France) – 1998 – 34 pages, режим доступу до статті: netlab.caltech.edu/FAST/references/bonald_comparison.pdf – Час доступу: січень 2013 р.
6. A control theoretic analysis of RED [Електронний ресурс] / C.V. Hollot, Vishal Misra, Don Towsley and Wei-Bo Gong - Режим доступу до статті: ftp://gaia.cs.umass.edu/pub/MisraInfocom01-RED-Control.pdf – Час доступу: січень 2013 р.
7. Jacobson, V. Congestion Avoidance and Control/ V. Jacobson - Proceedings, SIGCOMM '88, Computer Communication Review, August 1988; reprinted in Computer Communication Review, January 1995; a slightly revised version is available at ftp.ee.lbl.gov/ papers/congavoid.ps.Z.
8. Jacobson, V. Modified TCP Congestion Avoidance Algorithm/ V. Jacobson - End2 end-interest mailing list, 20, April 1990. Available at ftp://ftp.ee.Lbl.gov/email/vanj.90apr30.txt
9. Srikant, R. The Mathematics of Internet Congestion Control (Systems and Control: Foundations and Applications)/ Rayadurgam Srikant – Birkhauser Boston, 2004
10. Батыр С.С., Хорхордин А.В. Построение модели сети передачи данных для исследова-ний технологии AQM // Сборник научных трудов ДонИЖТ Выпуск:28 .- Донецк, 2011 С.108-116