Ebru Ozbay, Muhsin Tunay Gencoglu - Load Frequency Control for Small Hydro Power Plants Using Adaptive Fuzzy Controller

Abstract

Electrical energy generation is very important due to the increasing energy need. To satisfy the need, small scale hydro power plants are constructed in addition to large scale hydro power plants. Hydro power plants have a significant role in the generation of electrical energy. Small hydro power is a kind of clean and renewable energy sources. Small hydro power has a big potential in most areas of the world. This article proposed a novel model design for small hydro power plant (SHPP) using linear and nonlinear turbine model without surge tank effects. The model was created using adaptive fuzzy logic controller. The aim of this article is to improve their implementations by developing a SHPP model without using conventional control methods. The conventional control methods require choosing individual P and I parameters for each load value whereas in the developed model this process carried out by means of a single equations by using adaptive fuzzy logic controller.

I. INTRODUCTION

In electric power generation, small SHPPs have special importance caused by their low administrative, executive costs, and short construction time compared to large power plants [1]. A SHPP consists of diversion dam, conveyance of water system, forebay, penstock, wicket gate, power house, tailrace structure of the body and electrical and mechanical equipments [2]. SHPPs are generally isolated from grid network. SHPPs have some problems. These are; their storage potential is very small, unit cost is high and it affects quickly a small change in the regime of river. But the main problem on these plants is to keep the constant speed value. Frequency is an important criterion in electric power systems. The consumers want continuous, stabile, quality and reliable energy. For a power system, constant frequency and active power balance must be provided. If the active power balance is provided on the change of instantaneous power, frequency control can be provided [3,4]. In a power system operation such as SHPP, loadfrequency control is very important for supplying efficiently electrical power of good quality. Many control techniques have been used for this operation [5,6]. The conventional PID controllers are not suitable for complex, nonlinear, uncertain, high-order and time-delay systems. As an alternative to conventional control methods, the fuzzy logic that Zadeh first presented in 1965 has been studied for modeling of the complex systems in the past few decades and fuzzy logic controllers have been widely used to nonlinear, complex and uncertain systems such as engineering problems, robotics, renewable energy, signal processing, power electronics and modeling [7,8].

II. DEVELOPMENT OF SMALL HYDRO POWER PLANT MODEL

A. Mathematical Model Kinetic energy of the water is converted mechanical energy by turbines and the mechanical energy is converted to electrical energy by synchronous generators in the hydro power plants. There are two basic types of hydraulic turbines. These are impulse turbines and reaction turbines. The dynamic of hydraulic turbines have a significantly influence on the dynamic stability of the power system. The performance of a hydraulic turbine is influenced by the characteristics of the water column feeding the turbine. These include the effects of water inertia, water compressibility and pipe wall elasticity in the penstock. The effect of water inertia is to cause changes in turbine flow to lag behind changes in turbine gate opening. Travelling waves of pressure is the effect of elasticity in the pipe. This phenomenon is commonly referred to as “water hammer”. Therefore, water hammer effects are relatively insignificant for short penstock. Hydro power plant models are classified in form of linear and nonlinear models. These models can be divided into two groups; the turbine model assuming elastic water column and inelastic water column. 1) Linear Turbine Model: In linear model, the hydraulic resistance is negligible, the penstock pipe is inelastic and the water is incompressible. The velocity of the water in the penstock and turbine mechanical power is given by

Ku and Kp are constants of proportionality [9]. Tw called as water time constant or water starting time and its value varies between 1-4 s. Tw is 1 s for low head, 2.2 s for medium head and 4 s for high head [2]. Tw is defined as

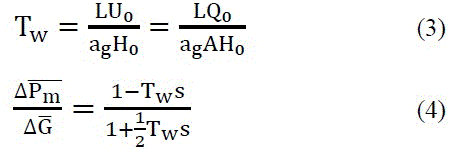
Equation (4) is the classic transfer function of hydraulic turbine. 2) Nonlinear Turbine Model Assuming a Inelastic Water Column: The model is constructed assuming an incompressible fluid and a rigid conduit. The friction head loss in the penstock is given by

From the laws of momentum, the rate of flow change in the conduit is

The conduit head losses (H) can be ignored in the models for simplicity. The per unit (p.u.) value of the turbine power output is:

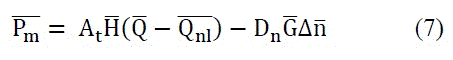
Where D is the turbine damping factor and its value varies between 0.5 and 2. Damping effects can be neglected in the model. If the turbine net head changes the turbine flow rate will also change. The p.u. flow rate through the turbine is

The turbine gain A is

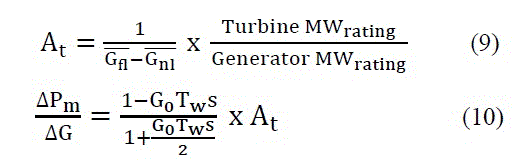
Equation (10) is nonlinear turbine transfer function which is linearized in the operation point. The linearized equations are suitable for computer applications [10-15]. B. Fuzzy Controlled System The fuzzy controllers are suitable for white-box problems, based on expert knowledge of the system. Fig.1. shows block diagram of a fuzzy controller. A fuzzy controller consists of four main components as fuzzification, rule base, inference mechanism and defuzzification. The fuzzification converts its inputs into fuzzy values with membership functions in the form of triangle, trapezoid, bell or other appropriate forms expressed by the fuzzy linguistic variables. The rule base contains the expert’s linguistic descriptions expressed in the form of logical implications such as IF x is positive THEN y is big. The inference mechanism evaluates fuzzy information to activate and apply control rules. The defuzzification that uses methods such as centre of gravity, maximum and weighted mean converts from the inference mechanism into the crisp values applied to the actual system [16-19]. K1, K2 and K3 are called as scaling factors in Fig. 1. Input and output scaling factors in the fuzzy controllers are important for providing to fire of appropriate rules independent from physical domain of the input and output signals. The scaling factors can be tuned to obtain maximum control performance.

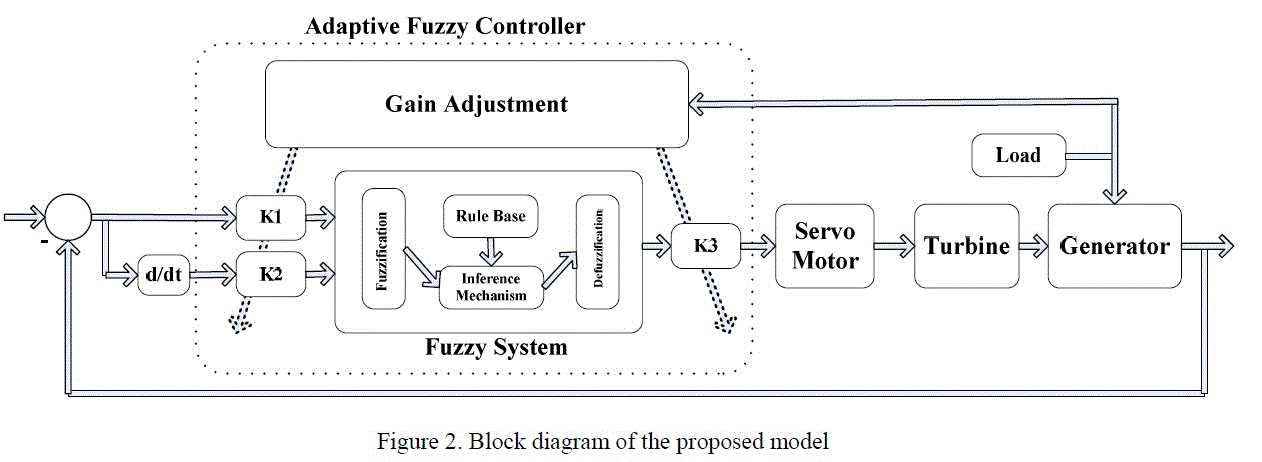
C. Adaptive Fuzzy Control System The proposed model of a SHPP is shown in Fig. 2. The model consists of regulator, servomotor, turbine and generator. The adaptive fuzzy controller is used as regulator. The scaling factors of the fuzzy controller are tuned with load information. There are two inputs and one output of the fuzzy controller. The first input is the error between reference value that is desired output value and generator output value. The second input is the derivative of the error. The inputs are given by

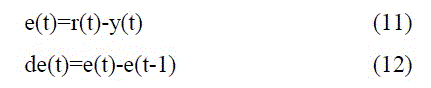
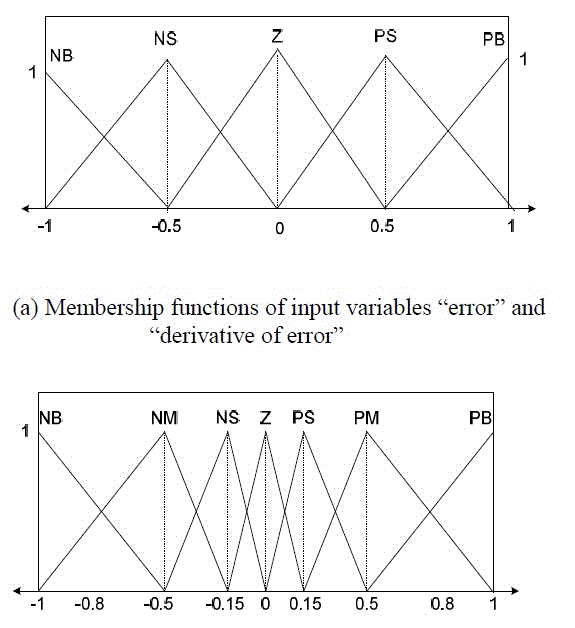
The inputs and output are multiplied by the scaling factors K1, K2 and K3, respectively. The design of the fuzzy controller depends on information about the system behavior or experience of a human expert. The fuzzification stage is determined by the choice of the range, shape and number of the membership functions. The output membership functions are chosen to be nonuniformly distributed seven triangular functions in order to minimize the computation time. The input membership functions are chosen to be uniformly distributed five triangular functions The range of the input and output membership functions is chosen in [-1, +1]. Input scaling factors are used to normalize the input magnitude. The membership functions of the input and output variables are shown in Fig. 3 (a) - (b). The fuzzy controller is used the max-min inference method that called as the Mamdani type inference. Defuzzification method is chosen as centre of gravity method. The parameters of the fuzzy controller are shown in Fig. 3.

The input and output scaling factors must be adjusted in order to make the fuzzy controller more sensitive to changes in the system. The input values of the fuzzy controller would range between [-1, +1]. In the proposed algorithm, many simulations have been performed to find optimum values of the scaling factors. Thus, the appropriate values of the scaling factors have chosen in different load conditions. And a polynomial function has fit using these values [20,21]. The functions used for gain adjustment in the proposed algorithm for linear and nonlinear turbine models are respectively shown in Fig. 4 (a) - (b).

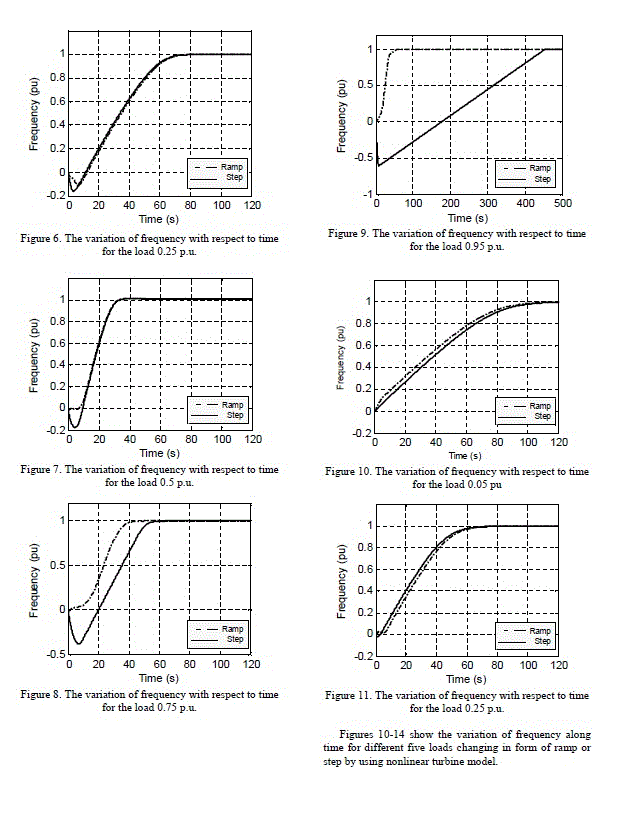
In this study, a load-frequency control based model using linear turbine and nonlinear turbine assuming inelastic water column was proposed for isolated SHPPs. The models were designed by using the Matlab-Simulink program. An adaptive fuzzy controller was applied to SHPP model as a governor. The controller regulates the wicket gate position according to the load. Because the water flow into the turbine is controlled by guide vane which is changed the gate position depend on the governor control signal. When some variations are appeared in the load, the controller regulates wicket gate position with servomotor. The servomotor open or close the gate until the produced and the desired electrical power is equal to each other. The servomotor regulated by controller is the governor of the system. Five different load values were used in this study; the values are 0.05, 0.25, 0.50, 0.75 and 0.95 p.u. All of the figures show comparatively the obtained simulation results for a step or ramp load changes. Primarily simulation results were obtained for linear turbine model. Fig. 5-9. present the variation of frequency along time for different five loads changing in form of ramp or step by using linear turbine model.

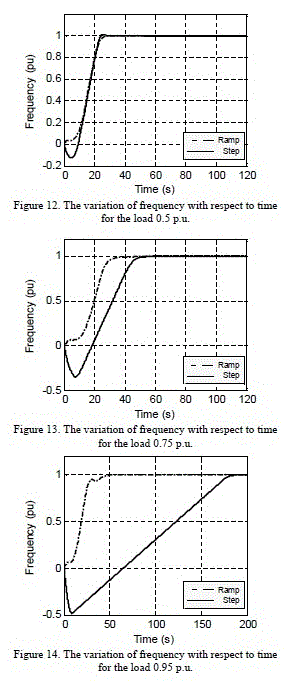
III. CONCLUSION There are many studies using different control methods for load frequency control in literature. In this article a novel alternative controller for load frequency control in an isolated SHPP was proposed. Comparisons between frequencies of step or ramp changes in the load were illustrated by figures. It was observed in comparison that the stabilizing time of frequency in the model with nonlinear turbine was shorter than that of the model with linear turbine and moreover the stabilizing time for ramp changes in the load was shorter than that of step changes in the load. The proposed adaptive fuzzy controller was easily adapted to different load values. For the simulation results, it was observed that the obtained results for small load change values in form of ramp or step was similar and when the load value increased the importance of ramp load revealed better. The stabilizing time takes long time because of water hammer and water inertia effects on the servo motor. These effects grow with increasing water time constant. Also when a change occurs in gate position turbine produces an opposite turbine power change. This effect is seen more on linear model.

Literaturverzeichnis

1.M. Hanmandlu, Himani Goyal, “Proposing a new advanced control technique for micro hydro power plants”, Electrical Power and Energy Systems, vol. 30, pp. 272–282, 2008.
2. S. Doolla, T.S. Bhatti, “Automatic generation control of an isolated small-hydro power plant”, Electric Power Systems Research, vol. 76, pp. 889–896, 2006.
3. O. Paish, “Small Hydro power: technology and current status”, Renewable & Sustainable Energy Reviews, vol.6, pp. 537-556, 2002.
4. M. Hanmandlu, “ An al based governing tecnique for automatic control of small hydro power plants”, ”, Institution of Electronics and Telecommunication Engineers, vol.53, pp. 119-126, 2007.
5. M. Hanmandlu, “ An al based governing tecnique for automatic control of small hydro power plants”, ”, Institution of Electronics and Telecommunication Engineers, vol.53, pp. 119-126, 2007..
6. Platz, J. (Projeksteuerung): Projektsteuerung, in: Platz, J./Schmelzer, H. J., Projektmanagement in der industriellen Forschung und Entwicklung, Berlin u.a. 1986 Raffel, A. (Entscheidungsfindung): Abweichungsinduzierte Entschheidungsfindung zur Steuerung von Software-Entwicklungen, Frankfurt a. M. 1988