Построение 3D модели кровеносных сосудов по серии КТ изображений печени.
Авторы: Артем М. Ятченко, Андрей С. Крылов, Андрей В. Гаврилов
Источник: http://imaging.cs.msu.su/pub/2009.Graphicon.Krylov.Liver.ru.pdf
Аннотация
Для планирования хирургической операции по пересадке фрагментов печени очень важно предоставить хирургу визуальную информацию о структуре кровеносных сосудов печени, их точном расположении внутри органа и о том, какие области печени омывает тот или иной сосуд. В данной статье для этого предлагается ряд методов построения и анализа объемных структур печени по серии рентгеновских компьютерных томографических снимков (КТ). В полуавтоматическом режиме сегментируются сосуды печени, строится скелет модели сосудов, по которому строится ориентированный граф, каждому ребру которого соответствует сосуд, а ориентации ребра – направление течения крови по нему. Интерактивно выделяются интересующие сосуды и сегментируется печень на области “омывания” этими сосудами.
1. ВВЕДЕНИЕ
При пересадке фрагментов печени пациенту пересаживают часть здоровой печени донора. Регенеративные свойства печени делают подобную операцию реальной. Однако очень важно заранее детально спланировать операцию – проверить совместимость донора с пациентом, определить области печени, подлежащие пересадке. 3D-представление кровеносных сосудов печени, а также визуальное отображение “омывания” тем или иным сосудом областей печени (рис. 1) повышает эффективность планирования [1].

Рисунок 1 – 3D-визуализация результата сегментации печени.
2. БИНАРИЗАЦИЯ
Первым шагом для построения 3D модели системы кровеносных сосудов является бинаризация изображения. Результатом бинаризации является 3D модель кровеносных сосудов. Перед КТ сканированием, для того, чтобы лучше выделить сосуды, в кровь пациента вводится специальное вещество, называемое контрастом. В результате данного действия сосуды на изображениях становятся более яркими (рис. 2).

Рисунок 2 – Серия КТ печени с введенным контрастом.
Для выделения кровеносных сосудов применяется итерационный алгоритм сегментации с переменным порогом яркости [2]:
- Доктором вручную выбирается стартовый пиксель p0 основания портальной вены (сосуда, по которому кровь притекает в печень). Его яркость принимается за начальный порог
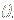 0 = I(p0).
0 = I(p0). - Выбирается примыкающая к p0 односвязная область пикселей, яркость которых не ниже текущего порога
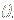 0, и эти пиксели заносятся в список.
0, и эти пиксели заносятся в список. - Строится примыкающая к L0 область с порогом
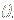 1 и пиксели этой области заносятся в список L1 = L(
1 и пиксели этой области заносятся в список L1 = L(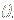 1,L0).
1,L0). - Шаги 3 и 4 повторяются до тех пор, пока не будет достигнут порог
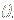 end.В качестве порога
end.В качестве порога 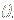 end выбирается средняя яркость печени.
end выбирается средняя яркость печени.
На данном этапе генеририруется множество списков L0,L1…Lend, соответствующих порогам ![]() 0,
0,![]() 1…
1…![]() end. Пример визуализации этих списков привед?н на рисунке 3. Доктору остается выбрать наиболее подходящий порог
end. Пример визуализации этих списков привед?н на рисунке 3. Доктору остается выбрать наиболее подходящий порог ![]() opt.
opt.

Рисунок 3 – 2D и 3D визуализация модели кровеносных сосудов при различных выбранных порогах.
3. ПОДГОТОВКА ДЛЯ СКЕЛЕТИЗАЦИИ
Результаты, полученные на современном оборудовании, таком как КТ и МРТ, характеризуются очень большим размером 3D-данных высокого разрешения. Для обработки таких массивов данных должны применяться методы уменьшения размеров массивов, при этом сохраняя максимально возможное количество информации. Один из таких методов – скелетизация объектов.
Прежде чем применять скелетизацию, объект нужно подготовить к этой операции. Поскольку скелетизация сохраняет структуру объекта, она сохранит также и полости внутри объекта, оставив на их месте “пузыри” (рис. 4 (a)).
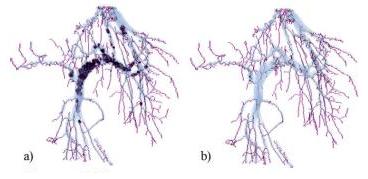
Рисунок 4 – Пример скелетизации системы кровеносных сосудов без предварительного заполнения дыр (a) и с предварительным заполнением дыр (b).
Рассматриваемый объект – сосудистое дерево и полостей внутри объекта быть не должно. Чтобы предотвратить появление “пузырей” в скелете, перед скелетизацией нужно избавиться от полостей, возникающих из-за шумов на снимках.
Для заполнения полостей используется алгоритм последовательного сканирования: пиксели фона разбиваются на группы связности и оставляются лишь группы, прилегающие к границам куба данных. Остальные группы маркируются как пиксели сосудов. Пример заполнения дыр при формировании скелета приведен на рис. 4.
4. СКЕЛЕТИЗАЦИЯ
Скелетизация в трехмерном пространстве довольно сложная задача. Существует множество алгоритмов скелетизации в двухмерном пространстве, однако для 3D их не так много (см. [3], [4], [5]).
Используем понятия 6-соседства, 18-соседства и 26-соседства (соседство по грани, по грани или ребру или по грани, ребру или вершине соответственно) [3].
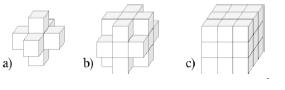
Рисунок 5 – a – множество N6(p), b – множество N18 (p) , c – множество N26(p).
Будем обозначать множество всех 6-соседей (18-соседей, 26-соседей) пикселя p как N6(p) (N18(p) , N26(p)) (рис. 5).
Пиксели, принадлежащие объекту, будем называют черными, а пиксели, принадлежащие фону – белыми.
Для пикселя p множество всех соседним с ним черных пикселей обозначим как S(p) (т.е. это множество всех черных пикселей из N26(p)\p). Множество всех соседних с p белых пикселей обозначим как ![]() .
.

Рисунок 6 – Пример соседних пикселей и соответствующая им диаграмма Шлегеля (соответствует виду сверху на p).
Диаграмма Шлегеля – схематическое планарное отображение соседних по 26-соседству с p пикселей (рис. 6).
Пиксель называется значимым, если при его удалении нарушается структура объекта, т.е. выполняется хотя бы одно из следующих условий:
- В N26(p) имеется не более одного черного пикселя.
- Множество S(p) и Not(S(p)) не связны.
Процесс скелетизации состоит в том, что удаляются все граничные не значимые пиксели до тех пор, пока такие пиксели существуют.
Для проверки пикселя на значимость, достаточно проверить количество его черных соседей и связность множеств S(p)и Not(S(p)), однако такая проверка занимает много времени. Ниже приведен более быстрый алгоритм проверки значимости пикселей.
Для выбранного пикселя p обозначим за n1 – количество вершин p, граничащих хотя бы с одним черным пикселем (кроме пикселя p), n2 – количество ребер p, граничащих хотя бы с одним черным пикселем (кроме p), а n3– количество граничных граней.
Числом Эйлера для окрестности S называется ![]() = n1 - n2 + n3. При этом, если пиксель p не является значимым, то число Эйлера для него равно 1. Обратное, в общем случае, неверно.
= n1 - n2 + n3. При этом, если пиксель p не является значимым, то число Эйлера для него равно 1. Обратное, в общем случае, неверно.
Если у пикселя есть только один сосед, то такой пиксель будем называть конечным и будем считать его значимым.
Чтобы проверить, является ли пиксель значимым или нет в том случае, когда число Эйлера ![]() = 1, достаточно рассмотреть 4 случая: n3 = 0, n3 = 1, n3 = 2 и n3 >2:
= 1, достаточно рассмотреть 4 случая: n3 = 0, n3 = 1, n3 = 2 и n3 >2:
- При n3 >2 пиксель не будет значимым.
- При n3 = 2 пиксель будет значимым, если либо существует изолированная вершина на диаграмме Шлегеля, либо n2 = 9.
- При n3 = 1 пиксель будет значимым, если существует изолированная вершина на диаграмме Шлегеля, либо n2 = 8.
- При n3 = 0 пиксель будет значимым, если существует изолированная вершина на диаграмме Шлегеля. Если изолированных точек нет (а также нет граней, т.к. n3 = 0), то на диаграмме присутствуют только ребра. Вариантов, когда пиксель значимый, в этом случае довольно много, но все эти случаи можно просчитать заранее и занести в таблицу размером 512 байт (всего ребер – 12, следовательно различных вариантов присутствия этих ребер может быть 2^12=4096 бит).
Справедливость случаев 1, 2 и 3 проверяется перебором всех вариантов соседей пикселя.
5. ПОСТРОЕНИЕ ГРАФА
После того как был получен скелет, количество рассматриваемых пикселей значительно уменьшилось при том, что сохранилась структура кровеносной системы.
Чтобы получить полную информацию о структуре модели, нужно построить ориентированный граф, каждому ребру которого соответствует сосуд, ориентации ребра – направление движения крови по сосуду, а вершинам – соединения сосудов или их окончания.
5.1. Построение графа
Все пиксели скелета разбиваются на пиксели, принадлежащие ребрам графа, и пиксели, принадлежащие вершинам графа. Все пиксели ребер объединяются в группы связности и каждая такая группа считается ребром.
Таким образом получается граф G = (V,E) (см. пример на рис. 7). Граф задается списком вершин V и списком ребер E.
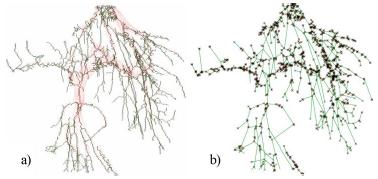
Рисунок 7 – a – скелет системы кровеносных сосудов, b – граф кровеносной системы.
5.2. Стрижка графа
Из-за шумов полученная модель исследуемой области может быть зашумленной. Частично дефекты убираются с помощью заполнения полостей, однако помимо них есть еще неровности стенок и сквозные отверстия в сосудах. Все эти шумы могут повлиять на структуру скелета. Такие ребра могут образовывать висячие ребра и циклы. Структуры, образованные шумами имеют размеры порядка толщины сосудов, что для кубов размером 512х512х512 пикселей обычно не превосходит 10 пикселей. Длины самих сосудов обычно составляют не менее нескольких десятков пикселей, так что избавиться от шумов можно разомкнув все маленькие циклы и убрав все короткие висячие ребра (стрижка).
На этапе стрижки размыкаются все циклы, длиной меньше порога ![]() 1 и удаляются все висячие ребра, длиной меньше
1 и удаляются все висячие ребра, длиной меньше ![]() 2.
2.
На последнем этапе стрижки из графа выбрасываются фиктивные вершины: если в одной вершине сходятся ровно 2 ребра, то вершину можно удалить, а ребра объединить в одно.
Результатом является граф, ребра которого соответствуют сосудам, а вершины – соединениям сосудов или концам сосудов (см. пример на рис. 8).

Рисунок 8 – Скелет и соответствующий ему граф до стрижки (a) и после стрижки (b).
6. ОРИЕНТИРОВАНИЕ ГРАФА
Каждому ребру полученного графа соответствует отдельный сосуд, а каждой вершине – ветвление сосудов либо окончание сосуда. Следующий этап – определить, в каком направлении течет кровь по сосудам.
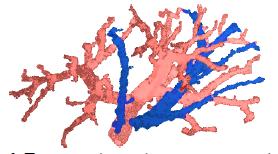
Рисунок 9 – Портальная (светлая) и печеночная вена (темная).
Сосудистая система представляет собой набор отдельных сосудистых деревьев (рис. 9). Граф G =(V,E) разбивается на несколько деревьев Gi, каждое из которых соответствует отдельному сосудистому дереву.
Основным критерием для ориентирования является то, что кровь теч?т от более широких сосудов к более узким.
6.1. Определение толщины сосудов
Для определения средней толщины сосудов 3D модель кровеносных сосудов разбивается на отдельные сосуды, и вычисляется среднее расстояние от границы каждого сосуда до его скелета.
Чтобы разбить всю модель на отдельные области, отнесем каждый пиксель модели к сосуду, соответствующему ближайшему участку скелета к этому пикселю (рис. 10).

Рисунок 10 – Пример выделения сосудов.
За среднюю толщину сосуда будем брать усредненное расстояние от всех пикселей границы сосуда до его скелета.
6.2. Разбиение графа на отдельные деревья
Итак, дан связный граф G, каждому ребру которого дано в соответствие положительное число – толщина соответствующего этому ребру сосуда. Требуется разбить граф G на несколько деревьев Gi со следующими условиями: корень каждого дерева должен совпадать с корнем сосудистого дерева, все пути внутри одного дерева от корня до висячих вершин соответствуют направлению течения крови по этим сосудам.
Сначала выбирается корень самого первого дерева G0. В качестве корня бер?тся самый толстый из имеющихся сосудов e0 и заносится в дерево G0. Затем рассматриваются все соседние с e0 сосуды и самый широкий из них e1 заносится в G0. Затем рассматриваются все соседние с e0 и e1 сосуды и выбирается самый широкий сосуд и так далее.
Если на очередном шаге из множества всех до сих пор неотмеченных сосудов самый широкий сосуд более чем в a раз (a > 1 – параметр метода) шире самого широкого из соседей дерева G0, то этот сосуд выбирается как корень нового дерева G1. В реализованном алгоритме a = 2.
Когда деревьев несколько – рассматриваются все примыкающие хотя бы к одному из деревьев ребра, и среди них выбирается самое широкое. Это ребро добавляется к тому дереву, к которому оно примыкает. Аналогично, если на каком-то шаге существует ребро, ширина которого больше чем в a раз превосходит самое широкое из граничащих ребер, то оно выносится как корень нового дерева.
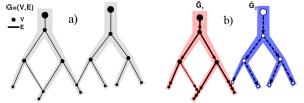
Рисунок 11 – a – граф двух пересекающихся сосудов, b – ориентированные деревья.
Ориентация ребер проходит от корня к висячим вершинам (рис. 11).
7. ИНТЕРАКТИВНАЯ СЕГМЕНТАЦИЯ СОСУДОВ
Врачу на экране монитора компьютера предоставляется визуальное представление 3D-модели сосудов и скелета, на котором он может указать основания интересующих его ветвей сосудов, присвоить им названия и раскрасить их в произвольные цвета (рис. 12).
8. ЗАКЛЮЧЕНИЕ
Разработанные методы встроены в станцию обработки и анализа медицинских данных АРИС MultiVox 5.5. Испытания работы алгоритмов в Российском Научном Центре Хирургии РАМН (лаборатории Нагрузочных тестов и Абдоминальных методов исследования) показали их пригодность для использования в качестве диагностических инструментов.

Рисунок 12: Выделенные сосудистые деревья (a) и вручную отсегментированные ветви (b).
Результаты использования разработанного алгоритма для планирования хирургических операций по пересадке фрагментов печени были представлены совместно с сотрудниками ГУ Российский научный центр хирургии им.Б.В. Петровского РАМН, в докладе на ХХ Всероссийском радиологическом съезде [6]. Работа выполнена при частичной поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009 – 2013 годы.
ЛИТЕРАТУРА
- Reitinger B., Bornik A. et al., Liver Surgery Planning Using Virtual Reality// IEEE Comp. Graph. & Ap., v. 5, 2006, p.36-47.
- Selle D., Preim B. et al., Analysis of vasculature for liver surgical planning// IEEE Med. Imag., v. 21, 2002, p. 1344 – 1357.
- Mian P., Gisela K., A revision of a 3D Skeletonization algorithm// CITR, Univ. Auckland, NZ, 2004 Res. Tech. Rep. 143.
- Antoine Manzanera, Thierry M. Bernard, n-dimensional skeletonization: a unified mathematical framework// J. of Electronic Imaging, v. 11, 2002, p. 25 – 37.
- Jonker P., Morphological Operations on 3D and 4D Images: From Shape Primitive Detection to Skeletonization// DGCI, 2000, p. 371-391.
- Ховрин В., Камалов Ю.Р., Ким Е.Ф., Филин А.В., Гаврилов А.В., Архипов И.В., Ятченко А.М., Первый опыт применения отечественной рабочей станции MultiVox 2D/3D для оценки ангиоархитектоники печени у потенциальных родственных доноров фрагментов печени// Тезисы докладов ХХ Всероссийского радиологического съезда, 2009, с. 53-56.