Обработка и анализ границ объектов на основе метода активных контуров.
Авторы: Семашко А.C., Крылов А.С.
Источник: http://imaging.cs.msu.su/pub/2010.DSPA.Semashko_Krylov.AC.ru.pdf
Аннотация
На основе метода активных контуров и метода опорных векторов предложен алгоритм анализа изображений, позволяющий выделить поврежденные участки границы объекта и получить аппроксимацию исходной неповрежденной границы на этих участках.
Постановка задачи
Для восстановления недостающих данных в изображениях разработано много алгоритмов, требующих для их применения информации о том, какая область изображения повреждена или содержит неверные данные. Очевидно, что невозможно построить общий метод определения таких областей. Поэтому для тех случаев, когда эти области неизвестны, необходимо разрабатывать алгоритмы, использующие всю имеющуюся информацию о повреждениях.
Целью данной работы является разработка полуавтоматического алгоритма, который выделяет границу объекта на изображении и анализирует найденную границу. На вход алгоритм получает изображение однотонного объекта, при этом для каждого объекта пользователь выставляет одну точку внутри этого объекта.
Тип повреждения гладкой границы объекта может быть одним из следующих:
- Полосы переменной ширины, в которых пиксели объекта имеют цвет фона (рис. 1а). Предполагается, что значения ширины каждой полосы (при дискретизации с шагом порядка размера пикселя) случайны и имеют известное (с точностью до значений некоторых параметров) распределение.
- Ложные данные в виде полос, расположенных вдоль границы объекта (рис. 1б). Аналогично первому типу, значения ширины этих полос случайны и имеют известное распределение.
- Несколько повреждений одного из описанных типов с различающимися параметрами.
- Несколько повреждений, каждое из которых может быть как первого, так и второго типа.

Рисунок 1 – Примеры повреждений.
Обзор алгоритма
Для решения поставленной задачи разработан алгоритм, включающий следующие шаги:
- Нахождение сглаженной границы объекта с помощью метода активных контуров [1];
- Получение прямоугольной «развертки» области изображения, содержащей границу;
- Анализ границы, выявление поврежденных участков с помощью метода опорных векторов SVM [2];
- Сглаживание полученного контура в тех областях, где граница повреждена.
Метод активных контуров
Метод активных контуров, или модель активных контуров, (англ. Active Contour
Model [1]) – вариационный метод поиска границ в изображении. В описываемом
алгоритме используется модель активных контуров свободной формы. В этой модели
задача поиска границы объекта формулируется как нахождение контура, на котором
некоторый функционал Е – «энергия» – достигает минимума. Модель имеет
динамический характер (в процессе минимизации энергии контур меняется), отсюда
название «активная». Поведение активного контура и его свойства полностью
определяются функционалом E. Энергия контура зависит от формы и размеров контура
и от его положения на изображении и записывается в виде суммы функционалов
«внутренней» и «внешней» энергии контура. Будем обозначать контур
![]() , а энергию E[v(s)] = Eint[v(s)] + Eext[v(s)], где Eext –
внешняя энергия, характеризующая «несоответствие» контура изображению, а Eint –
внутренняя энергия, реализующая требования к гладкости контура.
, а энергию E[v(s)] = Eint[v(s)] + Eext[v(s)], где Eext –
внешняя энергия, характеризующая «несоответствие» контура изображению, а Eint –
внутренняя энергия, реализующая требования к гладкости контура.
Если Eext не зависит от формы контура, ее удобнее интерпретировать как потенциал,
заданный на исходном изображении, а энергию контура записать в виде
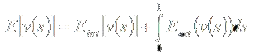 . При этом Eext получает смысл карты границ (edge map),
т.е. определяет на изображении области низкого потенциала, куда должен стремиться
контур для минимизации энергии.
. При этом Eext получает смысл карты границ (edge map),
т.е. определяет на изображении области низкого потенциала, куда должен стремиться
контур для минимизации энергии.
Пример: притягивание контура к тем областям изображения, где велики перепады яркости, обеспечивает внешняя энергия
где I(P) – интенсивность изображения в точке Р, I*G – свертка изображения с фильтром Гаусса.
Внутренняя энергия – регуляризующее слагаемое. Нами используется функционал вида [1]:
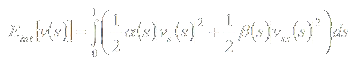
Такая энергия характеризует протяженность и изломанность контура.
Контур, доставляющий минимум функционалу энергии, должен удовлетворять уравнению Эйлера ![]() , которое можно рассматривать
как уравнение баланса сил
, которое можно рассматривать
как уравнение баланса сил ![]() , где Fext определяется моделью внешних сил.
Многие исследования были посвящены модели внешних сил; стоит отметить
результаты «Balloon Snake» [3, 4], GVF [5], BVF [6] и пр. Такую формулировку можно
рассматривать как обобщение исходной модели, которое и используется в данной
работе. Внешняя сила моделируется методом «Balloon Snake»: помимо внешней силы,
порожденной картой границ, в каждой точке контура действует сила, направленная по
внешней нормали к контуру в этой точке. В результате контур расширяется, пока не
попадет в область, где сила, порожденная картой границ, компенсирует расширяющую
силу.
, где Fext определяется моделью внешних сил.
Многие исследования были посвящены модели внешних сил; стоит отметить
результаты «Balloon Snake» [3, 4], GVF [5], BVF [6] и пр. Такую формулировку можно
рассматривать как обобщение исходной модели, которое и используется в данной
работе. Внешняя сила моделируется методом «Balloon Snake»: помимо внешней силы,
порожденной картой границ, в каждой точке контура действует сила, направленная по
внешней нормали к контуру в этой точке. В результате контур расширяется, пока не
попадет в область, где сила, порожденная картой границ, компенсирует расширяющую
силу.
Поле внешних сил, порождаемое картой границ (1) обладает свойством локальности: влияние пикселя изображения локализовано в окрестности фиксированного размера, зависящего от параметра фильтра Гаусса ?. Это ограничивает радиус захвата (capture range) границ, вне которого контур не испытывает влияния границы и не притягивается к ней. Один из способов борьбы с этим, широко применяющийся в настоящее время – использование нелокальных полей, таких как упомянутые выше GVF и BVF. В разработанном алгоритме используется другой способ, который позволяет исключить влияние поврежденных частей изображения. Вместо фиксации одного значения ?, поиск границы выполняется в несколько итераций, для каждой из них выбирается свое значение ? – наибольшее на первой итерации и монотонно убывающее по мере уточнения результата. Такой подход позволяет получить первое приближение решения, используя поле внешних сил с большим радиусом захвата, и последовательно улучшать решение, при этом на последних итерациях в неповрежденных областях изображения отсутствует влияние поврежденных областей.
Анализ границы
После нахождения границы нужно выделить на ней поврежденные участки. Для этого строится "развертка" границы I (рис. 2a), в которой каждому пикселю границы соответствует один столбец. Для каждого столбца развертки вычисляются признаки (рис. 2б), по которым с помощью метода опорных векторов (SVM) [2, 7] выявляются участки с повреждениями.
Для каждого пикселя границы по соответствующему столбцу развертки с номером x вычисляются значения
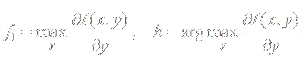
При классификации используются параметры f1 и f2 (вычисляется как стандартное отклонение значений h в некоторой окрестности данного пикселя границы).
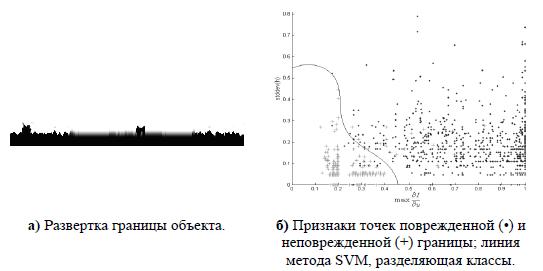
Рисунок 2 – Развертка границы объекта и признаки точек границы.
Результаты
Для построения контура, близкого к контуру исходного (неповрежденного) объекта, используется метод активных контуров с учетом результатов классификации. При этом внешние силы действуют только на те контрольные точки контура, которые находятся в неповрежденных областях. На остальные контрольные точки действуют только внутренние силы, что приводит к сглаживанию контура в поврежденных областях. Пример результатов восстановления контура показан на рис. 3в.

Рисунок 3 – Исходные данные и результаты.
Заключение
Разработан алгоритм анализа изображений для выделения поврежденных участков границы объекта и нахождения аппроксимации положения границы на этих участках. Конечная цель работы – разработать на основе данного алгоритма полностью автоматический метод восстановления изображений от повреждений описанного типа.
Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы и гранта РФФИ 09-07-92000-HHC.
Литература
- Kass M., Witkin A. and Terzopoulos D. "Snakes: Active Contour Models" // International Journal of Computer Vision. 1987. Vol. 1. pp. 321-331.
- Boser B. E., Guyon I. M. and Vapnik V. N. "A training algorithm for optimal margin classifiers" // Proceedings of the 5th Annual ACM Workshop on Computational Learning Theory. ACM Press, 1992. pp. 144-152.
- Cohen Laurent D. "On Active Contour Models and Balloons" // Computer Vision, Graphics, and Image Processing : Image Understanding. 1991. 53(2). pp. 211-218.
- Cohen L. D. and Cohen I. "Finite-Element Methods for Active Contour Models and Balloons for 2-D and 3-D Images" // IEEE Trans. Pattern Analysis and Machine Intelligence. 1993. 11: Vol. 15.
- Xu Chenyang and Prince Jerry L. "Snakes, Shapes, and Gradient Vector Flow" // IEEE Trans. Image Processing, vol. 7, no. 3, Mar. 1998. pp. 359-369.
- Sum K. W. and Cheung Paul Y. S. "A Fast Parametric Snake Model with Enhanced Concave Object Extraction Capability" // IEEE International Symposium on Signal Processing and Information Technology. 2006. pp. 454-457. ISBN: 0-7803-9753-3.
- Cristianini Nello and Shawe-Taylor John "An Introduction to Support Vector Machines and Other Kernel-based Learning Methods" Cambridge University Press, 2000. ISBN:0521780195.