Быстрый генетический алгоритм решения задачи кластеризации текстовых документов

В данной работе для кластеризации текстовых документов предлагается подход, суть которого заключается в одновременной минимизации диаметров кластеров и максимизации расстояний между кластерами. Предложенный подход сводится к задаче целочисленного программирования, которая решается с помощью генетического алгоритма. С целью повышения эффективности вводится штрафная функция, позволяющая ускорить процесс сходимости генетического алгоритма. В работе предложен критерий, определяющий оптимальное количество кластеров.

Введение

Последние годы в связи c быстрым ростом WWW многие научно-исследовательские работы направлены на организацию информации, чтобы помочь пользователям эффективно и точно находить желаемую информацию. Как известно, основная часть информации на Web представляется в текстовой форме (в HTML формате), которая является причиной обработки Web документов методами text mining. Применение методов data mining для извлечения знаний из текстовых данных называется text mining [1], [2]. Data mining включает много методов, позволяющих обнаружить естественную структуру в заданном наборе данных [3], [4]. Для обнаружения естественных групп в наборе данных кластеризация является одной из самых распространенных и полезных подходов в приложениях data mining [5], [6].

Кластеризация текстовых данных играет основную роль в областях text mining [7] и информационного поиска [8]. Цель задачи кластеризации состоит в разбиении набора текстовых документов на непересекающиеся группы (кластеры) с целью обеспечения максимальной близости (подобия) между документами одной группы, соответствующими определенной смысловой тематике, и максимального различия между группами [9]. Кластеризация текстовых документов первоначально была исследована для улучшения точности и полноты в системах информационного поиска. В дальнейших исследованиях область приложения кластеризации текстовых документов очень расширилась [10]:

• кластеризация документов, найденных механизмами поиска, с целью представления пользователю организованных результатов;
• кластеризация документов в коллекции (например, цифровые библиотеки);
• автоматизированное (или полуавтоматизированное) создание таксономии документов;
• эффективный поиск информации, сосредоточенной на релевантных подмножествах (кластеры), а не целые коллекции.

При кластеризации текстовых документов применяются разные методы и алгоритмы: деревья решения [11], статистический анализ [12-14], нейронные сети [15], генетический алгоритм [16-18], индуктивное логическое программирование [19], [20] и системы на основе правил [21], [22]. Следует отметить, что перечисленные методы и алгоритмы возникли на перекрестках разных научных областей исследований, в частности базы данных (Data Base), информационного поиска (Information Retrieval) и искусственного интеллекта (Artificial Intelligence), включающего машинное обучение (Machine Learning) и обработку на естественном языке (Natural Language Processing).

В данной работе для кластеризации текстовых документов предлагается подход, суть которого заключается в одновременной минимизации диаметров кластеров и максимизации расстояний между кластерами. Предлагаемый подход сводится к задаче целочисленного программирования, которая решается с помощью генетического алгоритма.

Постановка и математическая формулировка задачи кластеризации

Несмотря на разнообразие [4], [23-25] и область приложения [6-22], [26], [27], любой метод кластеризации состоит из четырех этапов: 1) модель представления данных; 2) выбор меры подобия; 3) создание модели кластеризации и 4) алгоритм кластеризации, который, используя модель данных и меру подобия, строит кластеры [10].

Пусть задан набор документов D=(D₁, D₂,..., D_n). Требуется кластеризация этого набора на непересекающиеся k кластеры C=(C₁, C₂,..., C_k) таким образом, чтобы документы в одном кластере были более близки друг к другу, чем документы в разных кластерах. Тогда C_q=∅ для q=1,...,k, C_q∩C_p=∅ для

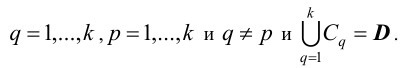
В отличие от других областей приложений, где задаются данные, т.е. не требуется особого труда построить модель представления данных, при кластеризации текстовых документов данные вычисляются с помощью модели TF*IDF (Term Frequency*Inverse Document Frequency). Идея моделирования TF*IDF заключается в представлении документа D_i в виде взвешенного вектора D_i=(ω_i1, ω_i2,...,ω_im). Здесь ω_ij – вес слова j в документе D_i, который определяется по формуле

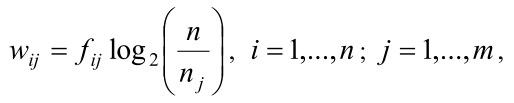
где n_j – число документов, в которых появляются слова j , m – число слов в наборе документов D , а ƒ_ij – функция частоты появления слова j в документе D_i, определенная формулой

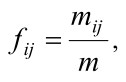
m_ij – число появления слова j в документе D_i.

Меру подобия между документами можно определить, используя одну из метрик – меру косинуса, евклидовую меру или меру Jaccard. Поскольку в данной работе близость будем определять геометрическим расстоянием, то для вычисления меры подобия между документами D_i и D_j используем метрику Евклида

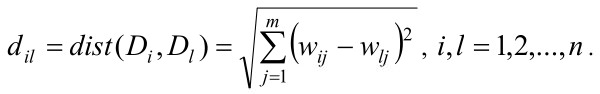
В зависимости от выбранного критерия процесс кластеризации может привести к различному разделению набора данных. Таким образом, при кластеризации выбор критерия является очень существенным.

Поскольку на основе идеи задачи кластеризации лежит отнесение близких документов в один кластер, то отсюда вытекает, что при правильной кластеризации диаметры кластеров должны быть в максимально возможной степени маленькими. Следовательно, при кластеризации необходимо минимизировать диаметры каждого кластера. Диаметр кластера C_q определяется следующей формулой:

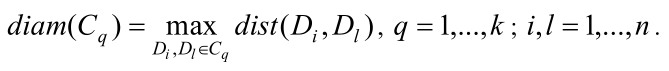
Из минимальности диаметра каждого кластера следует, что сумма диаметров кластеров также будет минимальной:

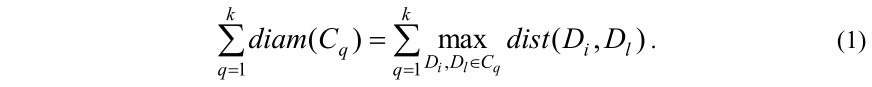
С другой стороны, очевидно, что при кластеризации расстояние между документами, отнесенными к разным кластерам, должно быть больше, чем расстояние между документами в одних кластерах. Расстояние между кластерами определяется формулой

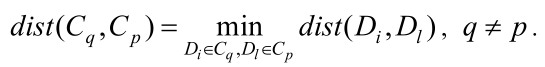
Суммируя по q и p (q≠p), получим сумму расстояний между кластерами:

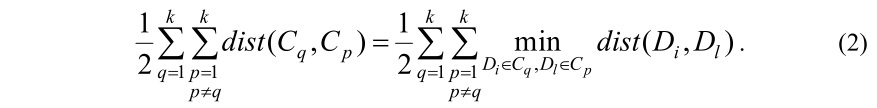
Таким образом, задача кластеризации документов сведена одновременно к минимизации суммы (1) и максимизации суммы (2). Другими словами, задача сведена к минимизации следующего соотношения:

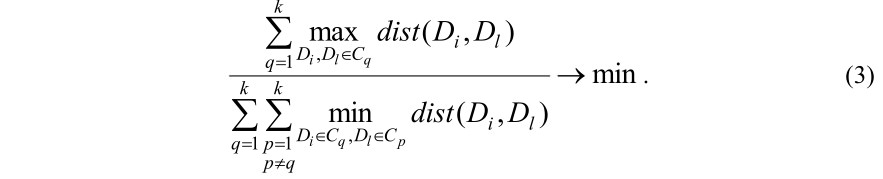
Пусть x_iq – булево переменное, равное 1, если документ D_i относится к кластеру C_q, или равное 0, в противном случае:

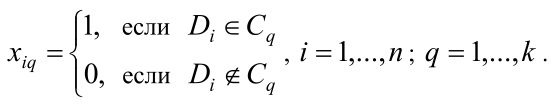
С учетом последнего обозначения задачу (3) записываем в следующем виде:

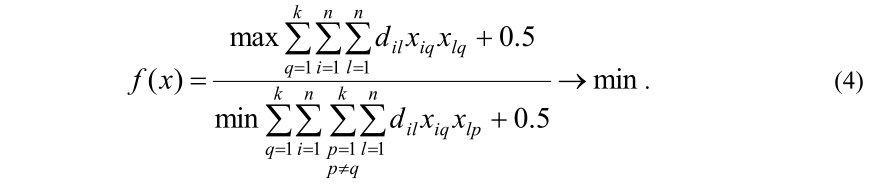
В последней формуле смещение 0.5 введено, чтобы избегать деления на нуль в случае, когда все документы одинаковые и кластеризированы в один кластер.

Из условия C_q∩C_p=∅, q≠p, следует, что каждый документ должен быть отнесен только к одному из q кластеров, т.е. должно быть удовлетворено следующее ограничение:

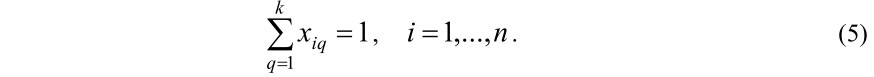
С другой стороны, при кластеризации подразумевается, что каждому кластеру должен быть отнесен хотя бы один документ C_q≠∅, тогда должно выполняться следующее условие:

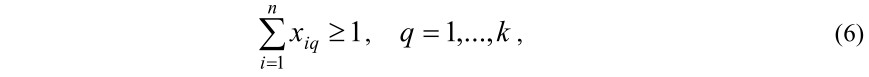
где

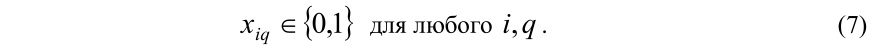
Итак, поставленная задача сведена к задаче целочисленного программирования (4) – (7), решение которого обеспечивает полную непересеченность кластеров. Известно, что большинство из них относится к задачам NP-полных. Поскольку решение таких задач требует больших вычислительных затрат, то с целью обеспечения практичности предлагается генетический алгоритм решения задачи целочисленного программирования.

Генетический алгоритм решения задачи целочисленного программирования

Несмотря на недостаток, который не гарантирует оптимальности найденного решения, генетические алгоритмы при решении задач дискретной оптимизации большой размерности, особенно при решении задач NP-полных, являются мощными инструментами. Это обусловлено тем, что при отыскании оптимальных решений генетические алгоритмы, в отличие от традиционных методов оптимизации, обеспечивают параллелизм, т.е. поиск решения ведется среди множеств альтернативных решений [28], [29]. Следовательно, с целью обеспечения практичности, когда требуется за определенное время найти одно или несколько субоптимальных решений, использование генетических алгоритмов является очень эффективным.

В генетических алгоритмах первым шагом является кодирование решений в виде хромосом, которое зависит от характера решаемой задачи. Поэтому, прежде чем использовать генетический алгоритм, сначала необходимо конструировать решения задачи в виде хромосомы. Исходя из характера решаемой задачи (4) – (7) хромосому в популяции представляем в таком виде: X=(x₁₁,...,x_1k, x₂₁,...,x_2k, x_n1,...,x_nk), где гены (переменные) x_iq(i=1,...,n; q=1,...,k) согласно (7) принимают значения 0 или 1. При таком кодировании размер хромосомы равняется n×k , где первая k позиция соответствует первому, следующая k позиция второму и т.д. документу. Например, при n=7 и k=3 кодирование X=(0,0,1,1,0,0,0,1,0,1,0,0,1,0,0,0,1,0,0,0,1) описывает ту кластеризацию, в которой документы D₁ и D₇ отнесены кластеру C₃(x₁₃=x₇₃=1), документы D₂, D₄ и D₅ отнесены кластеру C₁(x₂₁=x₄₁=x₅₁=1), а документы D₃ и D₆ отнесены кластеру C₂(x₃₂=x₆₂=1).

Следует подчеркнуть, что генетические алгоритмы легко применяются к задачам оптимизации без ограничения, а при решении задач с ограничениями генетические алгоритмы сталкиваются с проблемой появления недопустимых решений. Недопустимыми решениями являются те решения, которые нарушают ограничения (в нашем случае условия (5) и (6)) задачи. В процессе нахождения решения генетическим алгоритмом наиболее важной является постоянная поддержка допустимости решений в течение работы алгоритма, т.е. поддержание хромосом такими, чтобы они не нарушали ограничений (условий) задачи. Для предотвращения появления недопустимых хромосом предложены разные подходы [30-32]. Например, в работе [30] при появлении недопустимых решений предлагается совершать откат, возвращая хромосому в предыдущее состояние, а в работе [31] для получения допустимого решения к недопустимым хромосомам применяется функция коррекции. Наконец, в работе [32] предлагается подбор операторов скрещивания и мутации, применения, которые не приводят к появлению недопустимых хромосом. Во избежание от поддержания недопустимых хромосом в данной работе применяется метод штрафной функции, предложенный впервые в работе [33]. Эффективность метода штрафной функции в задачах оптимизации с ограничениями показана и в работе [34]. В работах [33], [34] было показано, что использование штрафной функции помогает быстрому нахождению решения и избегать преждевременной сходимости генетического алгоритма.

Идея метода штрафной функции заключается в ухудшении значений функции приспособленности (fitness function), при появлении недопустимых хромосом. Иными словами, если рассматривается задача минимизации, то введенная штрафная функция должна резко увеличивать значение fitness function. И наоборот, если решается задача максимизации, то штрафную функцию следует построить таким образом, чтобы она резко уменьшала значение fitness function.

Прежде чем построить штрафную функцию, вводим следующие обозначения:

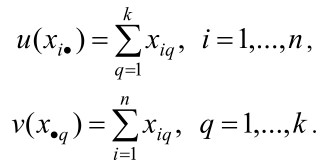
Так как (4) – (7) является задачей минимизации, то построенная штрафная функция при появлении недопустимых хромосом должна резко увеличивать значения fitness function. С учетом последнего высказывания штрафные функции построим следующим образом:

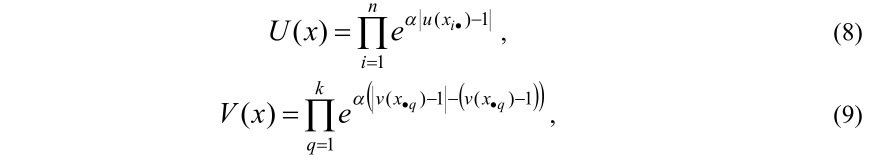
где α≥1называется коэффициентом ухудшения.

В формулах (8) и (9) функция U(x) предотвращает появление недопустимых хромосом, нарушающих условие (5), а функция V(x) предотвращает появление недопустимых хромосом, нарушающих условие (6).

Легко показать, что функции (8) и (9) отвечают следующим условиям:

• если условие (5) выполняется, то U(x)=1;
• если для некоторого i условие (5) не выполняется, то U(x)≥e^α;
• если условие (6) выполняется, то V(x)=1;
• если для некоторого q условие (6) не выполняется, то V(x)≥e^2α.

Следовательно, если оба условия (5) и (6) выполняются, т.е. решение является допустимым, то U(x)V(x)=1 , и наоборот, если хотя бы одно из этих условий не выполняется, т.е. решение недопустимое, то U(x)V(x)≥e^α.

Учитывая свойства штрафных функций, умножение целевой функции (4) на произведение U(x)V(x), задача (4) – (7) с ограничениями сводится к следующей задаче без ограничения:

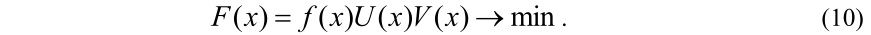
По другому хромосому можно конструировать в виде строки X=(y₁, y₂,...,y_n) длиной n, где аллели y_i пределяют номера кластера и принимают значение из множества {1,2,...,k}, а локусы (позиции генов) соответствуют номерам документов. На основе такого представления решение задачи определяется таким образом:

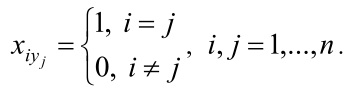
Например, X=(2,3,1,3,4,2,3) соответствует тому разделению, что документы D₁ и D₆ отнесятся к кластеру C₂(x₁₂=x₆₂=1), документы D₂, D₄ и D₇ относятся к кластеру C₃(x₂₃=x₄₃=x₇₃=1), документ D₃ относится к кластеру C₁(x₃₁=1) а документ D₅ отнесится к кластеру C₄(x₅₄=1)

Отметим, что при таком конструировании хромосом условие (5) всегда будет выполнено. В работе [32] было показано, что операторы скрещивания PMX (Partially Mapped Crossover) и мутации путем обмена (inversion mutation) не нарушают исходную структуру хромосомы, т.е. применение таких операторов к допустимым хромосомам не приводит к появлению недопустимых хромосом. Это эффективно только в том случае, когда начальная популяция генерирована при соблюдении условия (6). Поскольку число кластеризируемых документов намного больше количества кластеров n>>k, в таком случае при i₁≠i₂ имеет место y_i1=y_i2, то при генерации начальной популяции вероятность появления недопустимых хромосом будет очень велика. При этом время, потраченное на соблюдение условия (6), при генерации начальной популяции может быть сравнимо со временем решения задачи. Поэтому тут возникает целесообразность в применении метода штрафной функции. Так как условие (5) всегда выполнимо, то функция приспособленности будет иметь такой вид: F(x)=ƒ(x)V(x)→min.

Итак, методом штрафной функции недопустимые решения, порожденные операторами генетического алгоритма, в процессе ранжирования значений целевой функции будут отсеиваться, а допустимые решения будут иметь больше шансов на жизнь, т.е. метод штрафной функции позволяет ускорить процесс сходимости генетического алгоритма. Это следует из того, что метод штрафной функции при появлении недопустимых хромосом не требует выполнения дополнительных операций (совершать откат и возвращать хромосому в предыдущее состояние, производить коррекцию недопустимых хромосом и т.д.).

Теперь переходим к определению критерия останова, который является важным этапом генетического алгоритма.

Минимальность диаметра обусловливает, что точки в каждом кластере сосредоточиваются в окрестности центра. Поэтому определим координаты центров кластеров. j -я координата центра q-го кластера вычисляется формулой

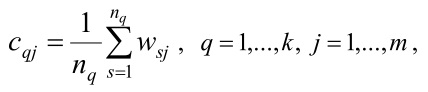
где n_q – число точек в q-м кластере. Очевидно, что

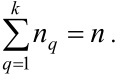
Среднее расстояние точек q-го кластера от центра вычисляется по формуле

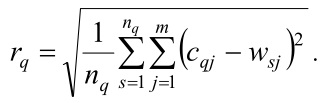
Из максимизации расстояний между документами, отнесенными к разным кластерам, следует, что центры кластеров будут удалены друг от друга. Среднее расстояние от каждого центра до остальных центров определяется формулой

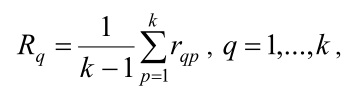
где r_qp – расстояние между центрами q-го и p-го кластеров.

Если отношение среднего расстояния до остальных кластеров к среднему внутрикластерному расстоянию для каждого кластера

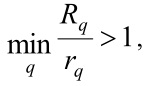
то следует остановить генетический алгоритм.

В отличие от классификации в задачах кластеризации не имеются предопределенные классы и примеры, которые показали бы, какие желательные отношения должны быть правильны среди данных; поэтому задача кластеризации воспринята как неконтролируемый процесс. Определение оптимального количества кластеров является одной из труднорешаемых задач, требующих особого подхода [35-42]. Здесь предлагается критерий, позволяющий определить оптимальное количество кластеров.

Легко видеть, что при k→n функция ƒ(x) стремится к нулю, т.е. она является монотонно убывающей функцией относительно k . Следовательно, имеется такое число k_*, при котором будет выполняться условие ƒ_k*-ƒ_k*-1<ε, где ε>0 – заданный допуск и ƒ_k* – значение функции ƒ(x) при k=k_*. Определенное таким способом k_* является оптимальным количеством кластеров. Из заданного алгоритма следует, что для определения оптимального количества кластеров, начиная с достаточно малого числа q, задача (4) – (7) решается неоднократно, пока заданный критерий завершения не будет удовлетворен. По другому количество кластеров можно определить алгоритмом, предложенным в [42].

Заключение

В данной статье предложен новый подход кластеризации текстовых документов, который математически формулируется в виде задачи целочисленного программирования. Как известно, в многомерном пространстве решение таких задач требует больших вычислительных затрат, поэтому с целью обеспечения практичности описывается генетический алгоритм решения задачи целочисленного программирования. Поскольку решение задач оптимизации с ограничениями с помощью генетического алгоритма сталкивается с проблемой постоянной поддержки хромосом, которая снижает процесс сходимости, то с целью ускорения сходимости генетического алгоритма вводится штрафная функция, которая предотвращает появление недопустимых хромосом при ранжировании значений функции приспособленности. В статье также описан пошаговый алгоритм определения оптимального количества кластеров. Отметим, что предложенный подход и генетический алгоритм решения задачи могут быть использованы в других областях, в том числе в медицине, биологии, физике и т.д.

Литература

1. Chakrabarti S. Data mining for hypertext: a tutorial survey //ACM SIGKDD Explorations. – 2000. – Vol. 1, № 2. – P. 1-11.
2. Chakrabarti S. Mining the web: discovering knowledge from hypertext data. – San Francisco. Morgan Kaufman, 2002. – 352 p.
3. Han J., Kamber M. Data mining: concepts and techniques. – San Francisco: Morgan Kaufman, 2000. – 550 p.
4. Grabmeier J., Rudolph A. Techniques of cluster algorithms in data mining // Data Mining and Knowledge Discovery. – 2002. – Vol. 6, № 4. – P. 303-360.
5. Fayyad U.M., Piatetsky-Shapiro G., Smyth P., Uthurusamy R. Advances in Knowledge Discovery and Data Mining. – Cambridge: AAAI/MIT Press, 1996. – 625 р.
6. Au W-H., Keith C.C.C., Wong A.K.C., Wang Y. Attribute clustering for grouping, selection, and classification of gene expression data // IEEE/ACM Transactions on Computational Biology and Bioinformatics. – April-June 2005. – Vol. 2, № 2. – P. 83-101.
7. Neto J.L., Santos A.D., Kaestner C.A.A., Freitas A.A. Document clustering and text summarization // Proceedings of the 4th International Conference on Practical Applications of Knowledge Discovery and Data Mining (PADD-2000). – Manchester. (UK). – April 11-13. – 2000. – P. 41-55.
8. Desai M., Spink A. An algorithm to cluster documents based on relevance // Information Processing and Management. – 2005. – Vol. 41, № 5. – P. 1035-1049.
9. Steinbach M., Karypis G., Kumar V. A comparison of document clustering techniques // Technical Report TR 00-034. Department of Computer Science and Engineering. – USA. University of Minnesota, May 2000. – 20 р.
10. Hammouda K.M., Kamel M.S. Efficient phrase-based document indexing for web document clustering // IEEE Transactions on Knowledge and Data Engineering. – 2004. – Vol. 16, № 10. – P. 1279-1296.
11. Nahm U.Y., Mooney R.J. A mutually beneficial integration of data mining and information extraction // Proceedings of the 17th National Conference on Artificial Intelligence (AAAI-00). – Austin. (USA). – July 31-Avgust 2. – 2000. – P. 627-632.
12. Ko Y., Seo J. Automatic text categorization by unsupervised learning // Proceedings of the 18th International Conference on Computational Linguistics (COLING’2000). – Saarbrucken (Germany): Morgan Kaufmann. – July 31-August 4. – 2000. – Vol. 1. – P. 453-459.
13. Caropreso M.F., Matwin S., Sebastiani F. Statistical phrases in automated text categorization // Technical Report IEI-B4-07-2000. – Pisa (Italy). – 2000. – 18 p.
14. Ko Y., Park J., Seo J. Improving text categorization using the importance of sentences // Information Processing and Management. – 2004. – Vol. 40, № 1. – P. 65-79.
15. Honkela T., Kaski S., Lagus K., Kohonen T. WEBSOM-self-organizing maps of document collections // Proceedings of the Workshop Self-Organizing Maps (WSOM’97). – Helsinki (Finland). – June 4-6. – 1997. – P. 310-315.
16. Maulik U., Bandyopadhyay S. Genetic algorithm-based clustering technique // Pattern Recognition. – September 2000. – Vol. 33, № 9. – P. 1455-1465.
17. Lu Y., Lu S., Fotouhi F., Deng Y., Brown S. Fast genetic k -means algorithm and its application in gene expression data analysis // Technical Report TR-DB-06-2003 // http://www.cs.wayne.edu/~- luyi/publication/tr0603.pdf. 2003. – 18 p.
18. Pan H., Zhu J., Han D. Genetic algorithms applied to multi-class clustering for gene expression data // Genomics Proteomics Bioinformatics. – 2003. – Vol. 1, № 4. – P. 279-287.
19. Junker M., Sintek M., Rinck M. Learning for text categorization and information extraction with ILP // Proceedings of the First Workshop Learning Language in Logic. – Bled (Slovenia). – 30 June. – 1999. – P. 84-93.
20. Yang Y., Slattery S., Ghani R. A study of approaches to hypertext categorization // Journal of Intelligent Information Systems. – 2002. – Vol. 18, № 2. – Pages 219-241.
21. Soderland S. Learning information extraction rules for semi-structured and free text // Machine Learning. – 1999. – Vol. 34, № 1-3. – P. 233-272.
22. Sebastiani F. Machine learning in automated text categorization // ACM Computing Surveys. – 2002. – Vol. 34, № 1. – P. 1-47.
23. Jain A.K., Murty M.N., Flynn P.J. Data clustering: a review // ACM Computing Surveys. – 1999. – Vol. 31., № 3.
24. Halkidi M., Batistakis Y., Vazirgiannis M. On clustering validation techniques // Journal of Intelligent Systems. – 2001. – Vol. 17. – № 2-3.
25. Jiang D., Tang C., Zhang A. Cluster analysis for gene expression data: a survey // IEEE Transactions on Knowledge and Data Engineering. – 2004. – Vol. 16, № 11.
26. Estivill-Castro V., Yang J. Fast and robust general purpose clustering algorithms // Data Mining and Knowledge Discovery. – 2004. – Vol. 8, № 2. – P. 127-150.
27. Giurcaneanu C.D., Tabus I., Astola J., Ollila J., Vihinen M. Fast iterative gene clustering based on information theoretic criteria for selecting the cluster structure // Journal of Computational Biology. – 2004. – Vol. 11, № 4. – P. 660-682.
28. Kureichik V.M. Genetic algorithms: state of the art, problems and perspectives // Journal of Computer and Systems Sciences International. – 1999. – Vol. 38, № 1. – P. 137-152.
29. Курейчик В.М., Родзин С.И. Эволюционные алгоритмы: генетическое программирование // Известия РАН. Теория и Системы Управления. – 2002. – № 1. – С. 127-137.
30. Глибовец Н.Н., Медвидь С.А. Генетические алгоритмы и их использование для решения задачи составления расписания // Кибернетика и системный анализ. – 2003. – № 1. – С. 95-108.
31. Витковски Т., Эльзвай С., Антчак А. Проектирование основных операций генетических алгоритмов для планирования производства // Проблемы управления и информатики. – 2003. – № 6. – С. 129-138.
32. Алгулиев Р.М., Алыгулиев Р.М. Генетический подход к оптимальному назначению заданий в распределенной системе // Искусственный интеллект. – 2004. – № 4. – С. 79-88.
33. Olsen A.L. Penalty functions and the knapsack problem // Proceedings of the First IEEE Conference on Evolutionary Computation. – Orlando (USA). – June 27-29. – 1994. – Vol. 2. – P. 554-558.
34. Lee Z-J., Su S-F., Lee C-Y., Hung Y-S. A heuristic genetic algorithm for solving resource allocation problems // Knowledge and Information Systems. – 2003. – Vol. 5, № 4. – P. 503-511.
35. Kothari R., Pitts D. On finding the number of clusters // Pattern Recognition Letters. – 1999. – Vol. 20, № 4. – P. 405-416.
36. Dudoit S., Fridlyand J. A prediction-based resampling method for estimating the number of clusters in a dataset // Genome Biology. – June 2002. – Vol. 3, № 7. – P. 1-21.
37. Bagirov A.M., Ferguson B., Ivkovic S., Saunders G., Yearwood J. New algorithms for multi-class diagnosis using tumor gene expression signature // Bioinformatics. – 2003. – Vol. 19, № 14. – P. 1800-1807.
38. Handl J., Knowles J. Multiobjective clustering with automatic determination of the number of clusters // Technical Report TR-COMPSYSBIO-2004-02. UMIST. – Manchester (UK). – August 2004. – 29 p.
39. Kim D.-W., Lee K.H., Lee D. On cluster validity index for estimation of the optimal number of fuzzy clusters // Pattern Recognition. – 2004. – Vol. 37, № 10. – P. 2009-2025.
40. Sun H., Wang S., Jiang Q. FCM-based model selection algorithms for determining the number of clusters // Pattern Recognition. – 2004. – Vol. 37, № 10. – P. 2027-2037.
41. Salvador S., Chan P. Determining the number of clusters/segments in hierarchical clustering/segmentation algorithms // Proceedings of the 16th IEEE International Conference on Tools with Artificial Intelligence (ICTAI 2004). – Boca Raton (USA). – November 15-17. – 2004. – P. 576-584.
42. Алгулиев Р.М., Алыгулиев Р.М., Багиров А.М.. Глобальная оптимизация в резюмировании текстовых документов // Автоматика и вычислительная техника. – 2005. – № 5 (в печати).

Р.М. Алгулієв, Р.М. Алигулієв

Швидкий генетичний алгоритм розв’язання задачі кластерізації текстових документів

У даній роботі для кластерізації текстових документів пропонується підхід, суть якого виводиться в одночасній мінімізації діаметрів кластерів і максимізації відстані між кластерами. Пропонований підхід зводиться до задачі цілочислового програмування, яка розв’язується з допомогою генетичного алгоритму. З метою підвищення ефективності вводиться штрафна функція, що дозволяє прискорити процес збіжності генетичного алгоритму. В роботі пропонується критерій, що визначає оптимальну кількість кластерів.

R.M. Alguliev, R.M. Aliguliyev

Fast genetic algorithm of the solution of the clustering problem of text documents

In this work for clustering of text documents the approach is proposed, essence of which consists in the simultaneous minimization of the diameters of clusters, and the maximization of the distances between the clusters. The approach proposed is reduced to the integer programming problem, which is solved with the aid of the genetic algorithm. Penalty function is introduced for the purpose of an increase in the effectiveness, making it possible to accelerate the process of the convergence of genetic algorithm. In the work the criterion, determining of an optimum number of clusters is suggested.