Белой О.И., Струнилин В.Н. - МОДИФІКАЦІЯ ІТЕРАЦІЙНОГО АЛГОРИТМУ КОМПОНОВКИ

УДК 681.3

МОДИФІКАЦІЯ ІТЕРАЦІЙНОГО АЛГОРИТМУ КОМПОНОВКИ

НА БАЗІ ГІПЕРГРАФОВОЇ МОДЕЛІ ЕЛЕКТРИЧНОЇ СХЕМИ

Білой О.І., Струнілін В.М.

Донецький національний технічний університет

кафедра комп’ютерної інженерії

Анотація:

Білой О.І., Струнілін В.М. Модифікація ітераційного алгоритму компоновки на базі гіперграфової моделі електричної схеми. Розглянуті алгоритми компоновки електричних схем в конструктивні елементи різних рівнів. Запропоновано модифікований ітераційний алгоритм компоновки, який більш ефективно, ніж стандартний метод, дозволяє виконувати компоновку при завданні електричної схеми у виді гіперграфу.

Загальна постановка проблеми

Компоновка - одна з основних процедур, що виконуються при конструкторському проектуванні РЕА [1]. Це процес переходу від електричної схеми до конструктивного розподілу (розбиттю) всіх елементів на групи, у відповідності до конструктивів різних рівнів, тобто процес перетворення функціонального опису апаратури в конструктивне.

Завданням компоновки є розрізання великої схеми, якою може бути структурна, функціональна, логічна, електрична принципова, на частини.

Відомо декілька груп алгоритмів компоновки [1, 2]. Як правило, в алгоритмах компоновки математичною моделлю об'єкту є граф, вершини якого відповідають модулям, а ребра — між модульним з'єднанням.

У послідовних алгоритмах спочатку вибирається перша вершина графа і послідовним приєднанням до неї інших вершин з числа нерозподілених (за умови задоволення заданим критеріям) формується перший шматок графа. Потім набирається другий шматок графа і так далі до повного розрізання.

Завдання компоновки найчастіше вирішується змішаними алгоритмами в два етапи: початкова компоновка послідовними алгоритмами і поліпшення результатів початкової компоновки ітераційними процедурами до задоволення прийнятих критеріїв.

Також останнім часом популярності набули еволюційні алгоритми або алгоритми генетичного пошуку [1]. Вирішуючи оптимізаційні завдання за допомогою генетичних алгоритмів, розробники спираються на модель простого генетичного алгоритму, який далеко не завжди дає бажані результати.

Ітераційні алгоритми розрізання застосовуються для поліпшення початкової компоновки, отриманої в результаті виконання послідовних алгоритмів. У графі, розрізаному на підграфи проводиться парна перестановка елементів різних підграфів з перевіркою на кожному кроці приросту числа ребер, що сполучають куски. Мета ітерацій — мінімізація числа сполучних ребер.

В даному алгоритмі необхідно знайти пару вершин x і ∈ X 1 , x j ∈E\ X 1 , для яких прирощення числа зовнішній зв’язків (ланцюгів) буде більше за 0 та максимальне.

maxΔ S ij = S ij − S ji >0 ;

S ij =|Γ X 1 ∩ΓE\ X 1 | , S ji =|Γ X 1 \ X i ∪ X j ∩ΓE\ X 1 \ X j ∪ X i | ,

де: X 1 - кусок матриці Q,

E\ X 1 - матриця Q без куска X 1 ,

S ij – число зовнішніх зв’язків між двома кусками до перестановки вершин i та j,

S ji – число зовнішніх зв’язків між кусками після перестановки вершин i та j.

Δ S ij =|Г X 1 ∩ГE\ X 1 |−|Γ X 1 \ X i ∪ X j ∩ΓE\ X 1 \ X j ∪ X i | .

Таким чином, матриця Q розбивається на 2 підматриці X 1 та E\ X 1 і для кожної пари вершин X ij розраховується Δ S ij . Потім серед усіх Δ S ij шукаємо найбільше додатне число і міняємо місцями i-ту та j-ту строки матриці. Далі знову розраховуємо Δ S ij для усіх можливих пар вершин підматриць. Якщо найбільше Δ S ij дорівнює нулю або негативне та закінчуємо компоновку.

Цей алгоритм досить легко запрограмувати, але він має суттєвий недолік – у кожному циклі необхідно заново розраховувати Δ S ij для усіх пар вершин підматриць, бо після того, як ми міняємо місцями строки матриці змінюється число зовнішніх та внутрішніх зв`язків кожного вузла схеми.

Ітераційний алгоритм компоновки гіперграфа на основі 4-х правил (Алгоритм 1)

Цей алгоритм на багато складніше запрограмувати ніж попередній і він потребує більше пам`яті у процесі роботи, але має суттєвий плюс – у кожному циклі необхідно розраховувати Δ S ij тільки для тих пар вершин які пов`язані ребрами з переставленими на попередньому кроці.

Суть ітераційних алгоритмів полягає у виборі деякого початкового «розрізання» початкового гіперграфу схеми на куски з подальшою мінімізацією числа ланцюгів між кусками за допомогою парного обміну вершин різних кусків. При цьому для кожної ітерації здійснюється перестановка тих вершин, які забезпечують максимальне зменшення числа зв'язків (ланцюгів) між парою кусків.

У роботах [3, 4] сформульовані умови знаходження приросту числа зовнішніх зв'язків (ланцюгів) Δ S ij при перестановці вершин e i ∈ G n , e j ∈ G m .

Для ланцюгу V k , інцидентному вершині e i , можливі наступні випадки:

1) ланцюг V k буде видалений з розрізу при перестановці пари елементів e i , e j , якщо E k ( E k =Г V k ) не містить e j і жодній з вершин з множини E n \ e i , тобто

( E k \ e i )∩( E n ∪ e j )=Ο ; (1)

2) ланцюг V k з'явиться в розрізі при перестановці пари елементів e i , e j , якщо E k не містить жодної з вершин множини E м , тобто

E k ∩ E m =Ο . (2)

Аналогічно для ланцюга V l , інцидентній вершині e j ∈ E ′ k :

1) ланцюг V l піде з розрізу при перестановці e i , e j , якщо E l ( E l =Г V l ) не містить вершини e i і жодній з вершин E m \ e j , тобто

( E l \ e j )∩( E m ∪ e i )=Ο ; (3)

2) ланцюг V l з'явиться в розрізі при перестановці вершин e i , e j , якщо E l не містить жодної з вершин множини E l , тобто

E l ∩ E n =Ο . (4)

Якщо одночасно не виконуються умови (3) і (4), то ребро V l залишиться в розрізі після перестановки e i , e j . Очевидно, що якщо ребро залишиться в розрізі, то воно не впливає на приріст Δ S ij і його можна не враховувати.

Δ S ij =( S − i + S − j )−( S + i + S + j ) , (5)

де: S − i , S − j - кількість ребер, які будуть видалені з розрізу;

S + i , S + j - кількість ребер, які з'являться в розрізу при перестановці вершин e i , e j .

На кожній ітерації знаходимо таку пару вершин e i , e j ( e i ∈ G n & e j ∈ G m ) , для якої

maxΔ S ij >0 .

Після обміну пари e i , e j значення ΔS необхідно перерахувати для пар вершин, суміжних з елементами e i ∪ e j . Алгоритм закінчується, коли Δ S ij ≤0 .

Модифікований ітераційний алгоритм компоновки гіперграфа (Алгоритм 2)

Матриця Q спочатку розбивається на підматриці Q 0 , Q 1 ,⋯, Q k , що відповідає розбиттю гіперграфа на шматки G 0 , G 1 ,⋯, G k . У підматриці Q 0 включаємо елемент e 0 , який відповідає роз’єму схеми. Розгледимо дві підматриці Q n і Q m , які відповідають шматкам G n і G m гіперграфа G. Виходячи з (1) – (4) можна сформулювати наступні правила, стосовно матриці Q [5].

Правило 1. Ланцюг V k залишається в розрізі при перестановці вершин e i , e j ∈E[ e i ∈ E n & e j ∈ E m ] якщо:

а) у стовпці V k матриці Q є два одиничні елементи в рядках e i , e j . У стовпці V l матриці Q є два одиничні елементи в строках e i , e j .

б) у стовпці V k матриці Q знайдеться два одиничні елементи (за винятком рядка e i ), один з яких належить підматриці Q n , а другий — Q m . У стовпці V l матриці Q знайдеться два одиничні елементи (за винятком рядка e j ), один з яких належить підматриці Q m , а другий — Q n .

Правило 2. Ланцюг V k піде з розрізу при перестановці вершин e i , e j , якщо в стовпці V k матриці Q один одиничний елемент знаходиться в рядку e i підматриці Q n , а усі інші одиничні елементи знаходяться в підматриці Q m . Ланцюг V l піде з розрізу при перестановці вершин e i , e j якщо в стовпці V l матриці Q один одиничний елемент знаходиться в рядку e j підматриці Q m , а усі інші одиничні елементи знаходяться в підматриці Q n .

Правило 3. Ланцюг V k з'явиться в розрізі при перестановці вершин e i ∈ E n , e j ∈ E m , якщо всі одиничні елементи знаходяться в підматриці Q n . Ланцюг V l з'явиться в розрізі, якщо всі одиничні елементи знаходяться в підматриці Q m .

Слід зазначити, що при виконанні правил 1(б), 2 і 3 в стовпці V k ( V l ) є один одиничний елемент в рядку e i ( e j ) .

Відмітимо, що при перестановці вершин e i , e j приріст Δ S ij знаходиться лише для шматків G n та G m і, відповідно, для підматриці Q n та Q m .

Ясно, що перевірка ланцюгів по правилах 1-3 значно простіше, чим по формулах (1) – (4) і потребує менше часу на реалізацію значень Δ S ij .

Тестування алгоритмів

Тестування алгоритмів проводилось випадково згенерованим гіперграфом з кількістю ребер та вершин від 10 до 100. При цьому гіперграфи “розбивались” на 2 - 10, 15, 20, 30, 40 та 50 кусків з рівною кількістю вершин у кожному. Результати досліджень залежності часу обчислення декількох з алгоритмів від розміру матриці приведені у таблиці 1.

Таблиця 1 – Залежність часу обчислення алгоритмів від розміру матриці Q

№	Потужність вершин X	Потужність ребер Е	Число вузлів	Час рішення, сек.
№	Потужність вершин X	Потужність ребер Е	Число вузлів	Алгоритм 1	Алгоритм 2
1	20	20	2	0,165	0,055
2	40	40	2	0,934	0,22
3	80	80	2	4,286	0,495
4	100	100	2	10,165	0,989
5	100	100	3	48,297	5,275
6	100	100	4	51,978	5,934
7	100	100	5	91,319	12,365
8	100	100	10	110,275	20,275
9	100	100	20	39,725	8,846
10	100	100	50	16,648	4,066

По результатах досліджень, наведених у табл. 1 можна зробити висновок, що швидкодія алгоритму 1 відносно алгоритму 2 не лінійна і залежить від багатьох факторів. Гістограма швидкості обчислення наведена на рис.1. Графік залежності часу обчислення графу від кількості вузлів у схемі при розбитті на 7 підсхем приведений на рис.2.

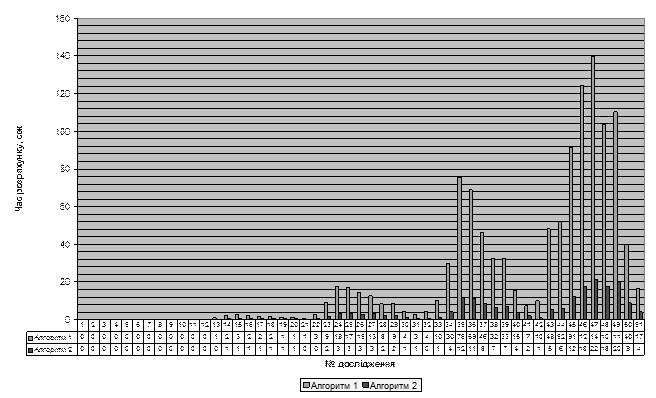
Рис.1. Гістограма швидкості обчислення алгоритмів, що досліджуються

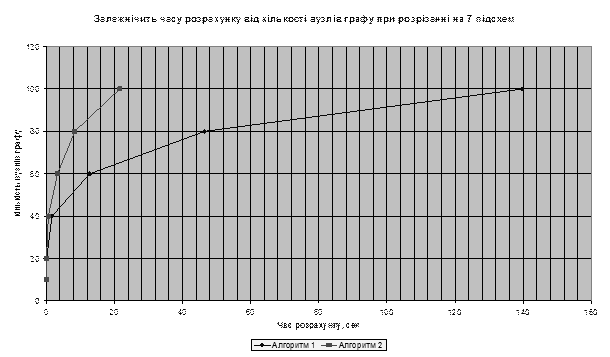
Рис. 2. Графік залежності часу розрахунку від розміру матриці при розрізанні

на 7 підсхем

Висновки

Гіперграфова модель є найбільш зручною формою представлення електричних схем у пам’яті комп’ютера. За допомогою цієї системи був досліджений пропонований алгоритм компоновки.

По результатах дослідження виявилось, що пропонований алгоритм дозволяє компонувати схеми в 2-20 разів швидше (чим більша кількість вершин у графі, тим більший коефіцієнт ефективності пропонованого алгоритму відносно стандартного) ніж стандартний ітераційний алгоритм компоновки. І це на схемах, які містять до 100 вузлів. На реальних схемах, число вузлів у котрих може сягати сотень тисяч або навіть мільйонів, цей показник може значно збільшитись. Запропонований алгоритм не потребує більше пам’яті у процесі роботи ніж стандартний, а також не поступається результативністю та надійністю.

Література

1. Курейчик, В. М. Математическое обеспечение конструкторского и технологического проектирования с применением САПР [Текст] / В. М. Курейчик. – М.: Радио и связь, 1990 . – 352 c.

2. Лебедев, Б. К. Методы поисковой адаптации в задачах автоматизированного проектирования СБИС: Монография / Б. К. Лебедев. – Таганрог: изд-во ТРТУ, 2000 . – 192 с.

3. Алексеев, О. В. Автоматизация проектирования радиоэлектронных средств: Учеб. пособие для радиотехн. спец. вузов [Текст] / Под ред. О.В. Алексеева. — М., 2000. — 479 с.

4. Мироненко, И. Г. Автоматизированное проектирование узлов и блоков РЭС средствами современных САПР: Учеб. пособие вузов / Под ред. И.Г. Мироненко. — М., 2002. — 391 с.

5. Саломатин, В.А. Итерационный алгоритм распределения конструктивных элементов при задании электрической схемы в виде гиперграфа [Текст] / В.А.Саломатин, В.Н.Струнилин // Наукові праці Донецького національного технічного університету. Серія «Інформатика, кібернетика і обчислювальна техніка» (ІКОТ-2008). Випуск 9 (132). — Донецьк: ДоНТУ. — 2008. — 316 с.