Тарутина Е.В., Мошкин Д.Г - ОЦЕНКА ЭФФЕКТИВНОСТИ АЛГОРИТМОВ КОМПОНОВКИ ПРИ ПРИНЯТИИ ПРОЕКТНОГО РЕШЕНИЯ

ОЦЕНКА ЭФФЕКТИВНОСТИ АЛГОРИТМОВ КОМПОНОВКИ ПРИ ПРИНЯТИИ ПРОЕКТНОГО РЕШЕНИЯ

Тарутина Е.В., Мошкин Д.Г. научный руководитель, доцент Носкова Е.Е.

Сибирский федеральный университет

Проведено исследование эффективности конструктивных и итерационных алгоритмов компоновки при принятии проектного решения в области конструирования электронных устройств. Выполнена оценка значений критериев оптимальности при компоновки коммутационных схем с различными параметрами. Построены графики зависимостей значений критериев оптимальности от параметров коммутационных схем. Проведен сравнительный анализ полученных данных на основе метода анализа иерархий и выявлены классы алгоритмов для расчета тех или иных типов коммутационных схем.

Источник: Сибирский федеральный университет

1. Введение. Для решения задач синтеза конструкций электронных устройств перспективными являются конструктивные и итерационные алгоритмы . Требование по ограничению площади, занимаемой коммутационными схемами на различных конструктивных уровнях, ведет к поиску новых конструкторских решений при их разработке. Высокая плотность размещения элементов в печатных узлах создает некоторые сложности при реализации соединений между ними. В ряде случаев определенным соединениям должно быть уделено особое внимание, поэтому при компоновке целесообразно локализовать некоторые цепи в пределах одного узла Оптимальная компоновка элементов обеспечивает повышение надежности печатн ых узлов, уменьшение размеров конструктивных единиц, минимизацию взаимны х наводок, уменьшение удельного тепловыделения и др.

Объектом автоматизации в данной работе является процесс конструирования электронных устройства при решении задачи компоновки. Объектом исследования является оценка показателей эффективности алгоритмов компоновки при изменении управляющих параметров для коммутационных схем заданного класса. Цель работы – оценка эффективности конструктивных и итерационных алгоритмов при решении задачи компоновки коммутационных схем электронных устройств.

2. Теоретическая часть. Компоновка - процесс перехода от электрической схемы к распределению (разбиению) всех элементов на функциональные узлы, соот-ветствующие конструктивам различных уровней. Основным для компоновки является критерий минимизации числа внешних соединений:

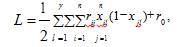(1)

Где r_ij- элементы матрицы соединений R, x_il-элементы матрицы переменных X, в которой x_il =1, если T_l ∈ e_i, x_il =0 в противном случае; n-число элементов коммутационной схемы; γ-число функциональных узлов; r₀ -внешние соединения

схемы.

Таким образом, задача компоновки заключается в минимизации функционала (1) при ограничениях на количество функциональных узлов и на количество элементов в узлах.

4. Описание эксперимента. К основным параметрам коммутационных схемам были отнесены: «процент маловыводных элементов» – характеризует количество выводов элемента;«процент средневыводных элементов» – характеризует количеств

выводов элемента;«процент многовыводных элементов» – характеризует количество выводов элемента; «процент малосвязных цепей» – характеризует количество выводов входящих в эту цепь;«процент среднесвязных цепей» – характеризует количество выводов входящих в эту цепь;«процент многосвязных цепей» – характеризует количество выводов входящих в эту цепь;

Для имеющейся выборки коммутационных схем была проведена их группировка в соответствии с вышеуказанными параметрами и выделено пять основных групп коммутационных схем:

· Малосвязные и малоэлементные;

· Среднесвязные и среднеэлементные;

· Многосвязные и среднеэлементные;

· Среднесвязные и многоэлементные;

· Многосвязные и многоэлементные.

Была проведена серия расчетов каждой группы схем алгоритмами компоновки : последовательный на основе разрезания графа; последовательный на основе матрицы цепей; итерационный на основе разрезания графа с заданной областью поиска; итерационный с минимизацией межузловых соединений; итерационный на основе разрезания графа с расширенной областью поиска. Алгоритмы разработаны на языке С++ в инструментальной среде Microsoft Visual Studio.

5. Результаты. Для выбора эффективного алгоритма компоновки с учетом основных параметров коммутационных схем была построена иерархия выбора алгоритма на основе матриц парного сравнения, приведенная на рисунке 1.

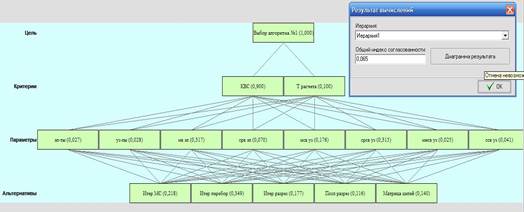
Рис.1 Иерархия выбора алгоритма

На основе построенной иерархии выполнен иерархический синтез в целях определения вектора приоритета альтернатив относительно факторов и фокуса иерархии.

6. Выводы. В результате проведѐнного исследования выделены параметров коммутационных схем, существенно влияющие на работу алгоритмов компоновки , определена количественная оценка работы каждого алгоритма для основных групп коммутационных схем. Эффективность последовательных алгоритмов компоновки доказана для многосвязных и многоэлементных схем, а итерационных алгоритмов - для малосвязных и малоэлементных схем заданного класса.