УДК 004.891
КОНЦЕПТУАЛЬНЫЕ «КАРКАСЫ» ОНТОЛОГИЙ В ПОДДЕРЖКЕ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
А.А. Кулинич
Институт проблем управления РАН, Москва
Исследуются вопросы поддержки построения онтологии плохо определенной предметной области по одному объекту из этой области. Предлагается метод, основанный на автоматическом построении концептуального «каркаса» предметной области и экспертном построении онтологии на основе этого «каркаса».
Введение
В настоящее время в системах поддержки принятия решений (СППР) все более широкое применение находят формальные модели экспертных знаний, представленные онтологиями разных уровней. Онтологический подход в СППР расширяет возможности поддержки принятия решений при решении множества классов задач, множеством различных методов.
Задачи поддержки принятия решений, решаемые в рамках онтологического подхода – это: поддержка выбора метода решения задач; классификация информации; интеграция разнородной информации; информационный поиск релевантной для поддержки принятия решения информации, интерпретация результатов решения задачи.
Узким местом при создании онтологической СППР в плохо изученной трудно формализуемой предметной области можно считать построение онтологий предметной области. Обычно онтологии строятся экспертом, но в последнее время появляются исследования автоматического построения онтологий на основе: анализа текстов, описывающих предметную область и на основе экспертно сформированном представительном множестве экземпляров предметной области.
В случае автоматического построения онтологии, на первом этапе построения осуществляется подбор текстов, отражающих основные закономерности предметной области. На следующем этапе применяют один из подходов лингвистического анализа выбранных текстов.
Качество подходов построения онтологии, опирающихся на автоматическую обработку текста, в значительной степени зависит от качества анализаторов текста. Известные теоретические трудности обработки естественного русского языка не позволяет говорить об их высоком качестве. Поэтому, онтологии предметных областей, получаемые автоматическим способом, основанные на лингвистическом анализе трудно верифицируемы, но могут быть использованы для поддержки работы экспертов при построении онтологии предметных областей.
Интерес также представляют работы по автоматизированному построению онтологий на основе экспертно сформированного представительного множества объектов предметной области. В работе [Baader, 2000] исследуются вопросы поддержки построения онтологии предметной области методом «Bottom-Top». Здесь выделяется представительное множество объектов предметной области, описанных на языке дескриптивной логики (ДЛ). Для выделенного множества объектов строится формальный контекст, а затем концептуальная решетка понятий – онтология - методами формального анализа понятий [Ganter, 1999].
К сожалению, в работе [Baader, 2000] не исследованы вопросы формирования представительного множества объектов для построения онтологии предметной области. Хотя, для построения онтологий плохо определенных предметных областей интересны методы их построения на основе небольшого количества объектов предметной области. В этой работе исследуется вопрос поддержки построения онтологии предметной области по информации об одном объекте из этой области. Предлагается формальными методами строить концептуальный «каркас» онтологии предметной области, который затем применяется в экспертной процедуре построения ее онтологии.
1. Концептуальный «каркас» онтологии предметной области
Обычный способ построения онтологии предметной области - экспертный. Эксперт, или группа экспертов определяют множество объектов, классов и понятий предметной области, их атрибуты, домены значений атрибутов, отношения между классами понятий, используя специальные программные среды разработки онтологий [Лапшин, 2010]. Если предметная область мало изучена экспертом, то и его знания, представленные в онтологии носят фрагментарный характер.
Рассмотрим одну из возможных моделей представления экспертных знаний о предметной области [Чечкин, 1991], которая может быть использована для описания знаний в условиях неопределенности. Здесь, все знания о предметной области представляется в виде некоторого множества сведений Х. Любые сведения об объекте этой предметной области (информация о свойствах объекта, значениях этих свойств) называется элементарным сведением об объекте и определяется тройкой: (p)di(x0)ÎХ, где (p)Î[1,0] – степень истинности наличия свойства di у объекта x0. Если сведение истинно (1), то его опускают при описании объекта, т.е. (1)di(x0)=di(x0)ÎХ.
Информация о том, что у объекта x0 нет свойства di, Ødi(x0) также считается сведением об объекте. Если у объекта x0 имеются два свойства d1(x0) и d2(x0), то конъюнкция и дизъюнкция этих свойств d1(x0)Ùd2(x0), d1(x0)Úd2(x0) также будут сведениями об объекте. Т.е., определены операции над элементарными сведениями di(x0) – (Ù, Ú, Ø), результаты которых также являются сведениями об объекте, d1(x0)Ùd2(x0)ÎХ, d1(x0)Úd2(x0)ÎХ. Утверждается, что все сведения об объекте образуют дистрибутивную решетку (L(x0), Ù, Ú), которая называется решеткой понятий. Информацией об объекте считается не просто множество элементарных сведений об объекте {di(x0)}, но и все возможные их обобщения, и сведения, полученные с помощью элементарных логических преобразований (Ù, Ú, Ø).
Основной вывод-утверждение, который следует из выше сказанного, заключается в том, что объект реального мира, определенный множеством элементарных сведений {di(x0)} порождает структуру сведений - решетку понятий (L(x0), Ù, Ú), которая несет информацию не только об объекте x0, но и информацию о предметной области и ее структурной организации. На этом утверждении основывается предлагаемый метод поддержки построения онтологии плохо определенной предметной области.
1.1. Необходимая структура онтологии предметной области
Среди многих определений онтологии выделим следующее: онтология предметной области – это кортеж: Оd=áC, A, R, Dñ , где C – множество классов (понятий) предметной области, A– множество атрибутов классов, R– отношение частичного порядка на множестве классов, RÍС´С, D – множество доменов (областей допустимых значений) атрибутов.
В онтологическом моделировании используют термины: класс (подкласс, надкласс), атрибуты класса, экземпляр класса. В дальнейшем мы будем использовать синонимичную терминологию, принятую в формальном анализе понятий: понятие, обобщенное понятие – это класс, надкласс; содержание понятия (признаки понятия) – это атрибуты класса; объем понятия – это множество экземпляров класса.
Определим понятие (класс) тройкой ádi,F(di),V(di)ñ, где di - имя понятия, F(di)={fij}- содержание понятия (множество признаков), V(di)={viq} - объем понятия, viq - объекты, имеющие признаки F(di).
Пусть B(F(di))={Æ, 2|F(d)|} - булеан содержания F(di) (множества признаков) некоторого понятия di, где 2|F(d)|, множество всех подмножеств содержания F(di). Известно, что элементы булеана образует частично упорядоченное множество по включении его элементов, т.е. решетку (B(F(di))£, Ù, Ú).
Любой элемент F(diH)ÎB(F(di)), HÎ[1,2|F(d)|], полученной решетки формально будем считать содержанием некоторого понятия diH обобщающего понятие di, если F(diH)ÍF(di). Кроме этого, отношение включения содержаний элементов решетки будем считать отношением «Класс-Подкласс» (Isa), при условии, что для объемов этих понятий выполняется достаточное условие V(di)ÍV(diH).
Решетку K(di)=(B(F(di))£, Ù, Ú) всех подмножеств содержания начального понятия di будем называть концептуальным «каркасом» онтологии плохо определенной предметной области. В концептуальном «каркасе» онтологии определены: абстрактные имена понятий diH (классов С); множество признаков понятия F(diH) (атрибутов классов А); отношения частичного порядка на множестве всех подмножеств содержания понятия F(di).
Концептуальный «каркас» считается необходимой структурой онтологии предметной области, к которой принадлежит начальное понятие di. Это означает, что атрибуты классов А={aj} онтологии предметной области Оd, построенной экспертом будут принадлежать концептуальному «каркасу» B(F(di)) объекта di этой предметной области, т.е. aj ÎB(F(di)), "j.
1.2. Достаточная структура онтологии предметной области
Для того чтобы концептуальный «каркас» K(di) превратить в онтологию предметной области Оd необходимо, чтобы формальному содержанию понятия F(diH) соответствовало бы множество реальных объектов предметной области – объем V(diH) ¹Æ, и было бы определено общепринятое имя обобщенного понятия diH.
В дескриптивной логике [Baader, 2004] понятие В
считается обобщением понятия А (В![]() А), если существуют экземпляры
обобщенного понятия, т.е. АIÍВI, ВI\АI ¹Æ, где АI ={aj} и ВI={bq} – интерпретации понятий А и В или иначе
множества их экземпляров aj и bq, j,q – индексы экземпляров, понятий А и В.
Если множество экземпляров обобщенного и необобщенного понятия совпадает ВI\АIºÆ, то имеем эквивалентность понятий АºВ, aj=bq," j,q.
А), если существуют экземпляры
обобщенного понятия, т.е. АIÍВI, ВI\АI ¹Æ, где АI ={aj} и ВI={bq} – интерпретации понятий А и В или иначе
множества их экземпляров aj и bq, j,q – индексы экземпляров, понятий А и В.
Если множество экземпляров обобщенного и необобщенного понятия совпадает ВI\АIºÆ, то имеем эквивалентность понятий АºВ, aj=bq," j,q.
В дальнейшем, достаточным условием существования (реальности) обобщенного понятия в концептуальном «каркасе» онтологии будем считать непустое множество разности объемов обобщенного и необобщенного понятия V(diH)\V(di) ¹Æ.
Виртуальным обобщенным понятием будем называть понятие, если разность объемов обобщенного и необобщенного понятия пустое множество, V(diH)\V(di) ºÆ.
2. Метод поддержки построения онтологии плохо определенной предметной области
В условиях неопределенности, когда число экземпляров предметной области невелико предлагается следующая экспертная процедура построения онтологии предметной области.
На первом этапе выделяется объект предметной области, для которого будет строиться концептуальный «каркас», с учетом следующих соображений. В дескриптивной логике (ДЛ) [Baader, 2004] на множестве экземпляров предметной области выделяются наиболее специфические объекты – msc (most specific concept). Эти объекты имеют более подробное описание их свойств (большее число признаков), записанных на языке ДЛ, по сравнению с остальными объектами.
Эксперт в качестве объекта предметной области, для которого будет строиться концептуальный «каркас» выбирает наиболее специфический объект vmsc, из множества наблюдаемых им объектов. Для такого объекта эксперт может определить большее число измеряемых признаков.
На втором этапе автоматически строится концептуальный «каркас» онтологии предметной области (B(F(dmsc)), Ù, Ú).
На третьем этапе экспертом определяется реальность обобщенных понятий diH (класс) по их содержанию F(diH) и имени необобщенного понятия dmsc (подкласс). Направление определения реальности понятий осуществляется по концептуальному «каркасу» снизу-вверх, от наиболее специфического понятия dmsc к его понятиям обобщения первого уровня, далее от обобщенных понятий первого уровня к обобщенным понятиям второго уровня и т.д.
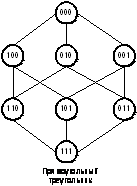
Пример результата экспертной процедуры построения онтологии геометрических фигур приводится в работе [Кулинич, 2006]. Здесь определен наиболее специфический объект - прямоугольный треугольник как: плоская геометрическая фигура; ограничена тремя сторонами; один угол прямой. Его содержание определено двоичным вектором, включающим три единицы (1,1,1). Все собственные подмножества множества признаков этого понятия также обозначаем двоичным вектором, в котором отсутствующие признаки обозначаются нулем. Например, двоичный вектор (1,0,1) определяет содержание понятия с двумя признаками: плоская геометрическая фигура и один угол прямой.
Концептуальный «каркас» прямоугольного треугольника приведен на рис.1. Онтология геометрических фигур, построенная на основе этого концептуального «каркаса» с использованием вышеописанных экспертных процедур приведена на рис.2.
|
Рисунок 1 - Концептуальный «каркас» прямоугольного треугольника |
Рисунок 2 - Онтология геометрических фигур |
3. Функциональные зависимости признаков понятий
Трудоемкость описанного выше метода построения достаточно высока. Избавить эксперта от определения виртуальных понятий можно, если учитывать закономерности строения наиболее специфического объекта предметной области. Эти закономерности выражаются функциональными зависимостями между признаками объекта.
В этом случае понятие определяем четверкой ádi,F(di),j(F(di)), V(di)ñ, где j(F(di)) – зависимость значений признаков понятия di .
Задание функциональной зависимости на множестве значений признаков означает, что множество всех подмножеств В(j(F(di))) содержания j(F(di)), будет подмножеством булеана В(F(di)), т.е. В(j(F(di)))ÍВ(F(di)). Из этого следует следующее утверждение: все подмножества содержания понятия с зависимостями его признаков В(j(F(di))) образуют частично упорядоченное множество по включению его элементов и следовательно, концептуальный «каркас» онтологии.
В качестве примера рассмотрим концептуальный «каркас» прямоугольного треугольника (Рис.1). Однако, второе свойство – геометрическая фигура «ограничена тремя сторонами» заменим другим определением – «ограничена тремя прямыми». Это определение позволяет сформулировать зависимость, выраженную правилом: j(F(di))=(Если Геометрическая фигура ограничена тремя прямыми, То она Плоская). Это правило порождает концептуальный «каркас», показанный на рис. 3 (отсутствуют узлы F(d3)=(011) и F(d5)=(010)).
|
Рисунок 3 - Концептуальный «каркас» |
4. Концептуальный «каркас» сложной предметной области
Рассмотрим сложные объекты предметных областей, которые могут быть декомпозированы на функциональные составные части.
Сложности моделирования отношений «Часть-Целое» в онтологиях связана с не транзитивностью некоторых видов этого отношения [Лукашевич, 2007]. Дело в том, что между свойствами частей и свойствами целого существуют функциональные зависимости, которые позволяют говорить об эмерджентности целого. Однако, сложные функциональные зависимости разнородных составных частей и целого, не могут быть описаны на ограниченном языке онтологий. Поэтому, обычно, при моделировании отношений «Часть-Целое» в онтологиях выбирают несложные функциональные зависимости, позволяющих осуществить вывод в онтологиях с отношением «Часть-Целое».
В этой работе рассматриваются вопросы построения концептуальных «каркасов» сложных объектов, свойства которых выражаются сложными функциональными зависимостями через свойства составных частей этого объекта.
Пусть субъект наблюдает сложный объект n некоторой предметной области X. Этот объект является элементом объема понятия, заданного тройкой: d, F(d), V(d) – соответственно, имя, содержание и объем понятия.
Пусть объект n может быть декомпозирован на составные части nQni, где Q - отношение «Часть-Целое», ni - функциональные составные части целого. Пусть определены, также, понятия di, F(di), V(di) – соответственно, имена, содержания и объемы понятий составных частей niÎV(di) и построены концептуальные «каркасы» понятия целого K(d) и всех его составных частей K(di), "i.
Задача
заключается в построении отображения всех n-ок
обобщенных понятий составных частей diH
в обобщенные понятия целого dH, т.е. Ф:![]() diH ® dH , где diH ÎK(di),"i, dH ÎK(d).
diH ® dH , где diH ÎK(di),"i, dH ÎK(d).
Все понятия концептуальных «каркасов» определены тройкой (имя, содержание, объем) и отображение Ф может быть построено при следующих допущениях:
1. Содержания всех обобщенных понятий целого могут быть выражены через содержания составных частей. Т.е. существует некоторая функция j такая, что F(dH)=j(F(diH));
2. В объем любого обобщенного понятия целого включаются объекты nHÎV(dH), составные части, которых есть объекты, включенные в объемы обобщенных понятий составных частей, т.е. niHÎV(diH). Это допущение означает, что обобщение составной части целого автоматически приводит к обобщению целого.
3.
Существуют имена обобщенных понятий целого dH , объем которого включает экземпляры, состоящие из
экземпляров, принадлежащих обобщенным понятиям составных частей. Т.е. $nHQ ![]() niH , где nHÎV(dH),
niHÎ
V(diH).
niH , где nHÎV(dH),
niHÎ
V(diH).
Первое и второе условия позволяют формальными методами по известным зависимостям свойств целого от свойств частей построить концептуальный «каркас» (необходимую структуру) и определить объемы всех обобщенных понятий целого, если известны объемы всех обобщенных понятий составных частей. Третье условие позволяет экспертным способом построить онтологию сложной предметной области на основе имеющегося «каркаса», при условии, что существует имя обобщенного понятий целого dH.
Например, рассмотрим сложный объект с признаками F(d)={g, h} и его двух составных частей d1 и d2 с признаками соответственно F(d1)={a,b,c} и F(d2)={d,e,f}. Пусть известно, что значения свойств целого g и h зависят от значений свойств составных частей следующим образом:
g=a Ù dÙ f ; h= c Ù e . (1)

Рис. 4 - Концептуальный «каркас» объекта
На рис. 4 показан концептуальный «каркас» этого объекта, включающий два типа отношений: отношение «Часть-Целое» (прерывистая линия); отношение «Класс-Подкласс» (сплошная линия). Отсутствующие в содержаниях обобщенных понятий признаки помечены двойным подчеркиванием.
С учетом зависимости признаков (1) содержания всех обобщенных понятий целого F(dH), выраженных содержанием обобщенных понятий составных частей F(diH), определится из следующих соотношений:
F(d)=gh=(F(d12)ÚF(d1))ÙF(d2); (2)
F(d1)=gh=(F(d12)ÚF(d11)ÚF(d14))Ù F(d22); (3)
F(d2)=gh=(F(d13)ÚF(d12)ÚF(d16))Ù (F(d22)Ú F(d23)Ú F(d25)); (4)
F(d3)=gh=(F(d15)ÚF(d17)ÚF(d14))Ù (F(d26)Ú F(d27)). (5)
При этом элементы объема nHÎV(dH)любого обобщенного понятия целого dH могут быть определены через элементы объема обобщенных понятий составных частей niHÎV(diH) с помощью следующих соотношений:
nQn12 Ùn2, где nÎ V(d), n12Î V(d1)ÚV(d12), n2Î V(d2); (6)
n1Qn14 Ùn22, где n1Î V(d1), n14Î V(d11) Ú V(d12), n22Î V(d22); (7)
n2Qn16 Ùn25, где n2Î V(d2), n16ÎV(d12)ÚV(d13), n25Î V(d25); (8)
n3Qn17 Ùn27, где n3Î V(d3), n17ÎV(d14)ÚV(d15), n27Î V(d26). (9)
Далее эксперт определяет имена обобщенных понятий целого dH, используя для этого не только его содержание F(dH), но и возможные составные части, определенные из соотношений (6-8).
Заключение
Предложенный метод поддержки деятельности эксперта при построении онтологии направлен активизацию его интеллектуальной деятельности и креативности на этапах построения онтологии плохо определенной предметной области.
Список литературы
[Baader, 2000] F. Baader and R. Molitor. Building and Structuring Description Logic Knowledge Bases Using Least Common Subsumers and Concept Analysis. In B. Ganter and G. W. Mineau, eds., Proceedings of the 8th International Conference on Conceptual Structures (ICCS 2000), volume 1867 of Lecture Notes in Computer Science, pp. 292-305. pringer-Verlag, 2000.
[Baader, 2004] Baader, F., Calvanese, D., McGuinness, D., Nardi, D., Patel-Schneider, P.F. The Description Logic Handbook: Theory, Implementation, and Applications.
[Ganter, 1999] Ganter, B. and Wille, R.: Formal Concept Analysis, Mathematical Foundations, Springer, 1999.
[Stumme, 2001] Stumme, G., Madche, A., 2001. FCA-Merge: Bottom-up merging of ontologies. In: 7th Intl. Conf. on Artificial Intelligence (IJCAI ’01). Seattle, WA, pp. 225–230.
[Лапшин, 2010] Лапшин В.А. Онтологии в компьютерных системах. – М.: Научный мир, 2010. – 224 с.
[Чечкин, 1991] Чечкин А.В. Математическая информатика. – М.: Наука. Гл. ред. Физ-мат. лит., 1991. – 416 с. – ISBN 5-02-014136-4.
[Кулинич, 2006] Кулинич А.А. Моделирование динамических процессов в понятийной системе субъекта для генерации креативных решений. Когнитивные исследования: Сборник научных трудов: Вып. 1/ Под редакцией В.Д. Соловьева. – 2006. с. 94-123.
[Лукашевич, 2007] Лукашевич Н.В. Моделирование отношения ЧАСТЬ-ЦЕЛОЕ в лингвистическом ресурсе для информационно-поисковых приложений. // Информационные технологии. - 2007. - N 12. Стр. 28 – 34.