УСТОЙЧИВОСТЬ АВТОМАТОВ К НЕИСПРАВНОСТЯМ ИХ ФУНКЦИИ ПЕРЕХОДОВ

Автор:О. М. Копытова
Источник: ISSN 1683–4720 Труды ИПММ НАН Украины. 2010. Том 21 УДК 519.71 с. 127–136.

Источник: УСТОЙЧИВОСТЬ АВТОМАТОВ К НЕИСПРАВНОСТЯМ ИХ ФУНКЦИИ ПЕРЕХОДОВ

Рассматривается задача сохранения поведения автомата при искажениях его структуры (графа переходов). Найдены условия, при которых искаженный автомат эквивалентен исходному по поведению.

Ключевые слова: автомат, поведение, переброска дуг, изоморфизм, идентификаторы.

Введение

1. Введение.Модель конечного автомата широко используется для описания систем и процессов преобразования информации. При этом формально различные модели таких систем могут обладать одним и тем же поведением. Такие различные модели могут возникать, например, в результате некоторых «неисправностей» систем, которые тем не менее, не искажают правильное функционирование автомата. Поэтому актуальной является задача анализа и сравнения поведения автоматов, соответствующих «неисправностям» системы–эталона. В рамках автоматной модели эта задача изучается в теории экспериментов с автоматами, технической диагностике, теории синтеза дискретных систем, где она является ключевой. В частности, эти вопросы становятся всё более актуальными в связи с широким внедрением различных микроэлектронных систем и компонент критического применения и повышенными требованиями к достижению необходимого уровня безопасности [1].

В теории абстрактных автоматов контрольные и распознающие эксперименты традиционно строятся для случая класса всех автоматов с n состояниями или его подклассов, где n – число состояний автомата–эталона. Многие такие классы можно описать как результат порождения класса автоматов из заданного автомата с помощью операции переброски дуг в его графе переходов. Например, класс локально порожденных автоматов [2], классы автоматов, порождаемых константными неисправностями в их схемной реализации, и ряд других можно описать указанным образом. Если при этом не меняются отметки дуг (пары вход–выходных символов), то такие переброски можно понимать как «неисправности» функции переходов автомата.

Однако в ряде случаев автоматы могут быть устойчивыми (по сохранению поведения) к искажениям структуры. В работе исследуется операция переброски дуг в графе переходов автомата Мили («неисправности» функции переходов) и ее влияние на изменение поведения автомата. Известно [3], что в результате переброски ровно одной дуги в приведенном автомате получается автомат, не изоморфный исходному, т.е. поведение «неисправного» автомата в этом случае всегда отличается от поведения исправного. Таким образом, всякий приведенный автомат оказывается неустойчивым к переброске ровно одной дуги. Для неприведенных атоматов это уже не так.

Представляет интерес задача изучения устойчивости приведенного автомата (в смысле сохранения поведения) при перебросках более, чем одной дуги. В работе изучается структура таких приведенных автоматов, которые устойчивы к неисправностям их функции переходов. Найдены необходимые условия в терминах поведенческих и структурных свойств графа переходов автомата, при которых переброска нескольких дуг в приведенном автомате приводит к автомату, эквивалентному исходному. Показано, что переброска с сохранением поведения допустима только для некоторых дуг, принадлежащих подграфам графа переходов, обладающих определенной симметрией.

Формальная постановка задачи.

Основные определения теории автоматов можно найти, например, в [4]. Под автоматом будем понимать автомат Мили A =(A,X, Y,δ, λ), где A,X, Y – алфавиты состояний, входов и выходов, соответственно, а δ, λ – функции переходов и выходов. Будем также рассматривать и частичные автоматы, у которых области определения функций переходов и выходов совпадают. Как обычно, будем обозначать автомат символом множества его состояний. Автомат A будем рассматривать также как множество дуг , где дуга – это четверка (s, x, y, t), если δ(s, x) = t,λ(s, x) = y. Функции δ и λ обычным образом распространяются на множество X∗ всех входных слов конечной длины.

Два состояния a и b одного и того же автомата A или двух разных автоматов, соответственно A и B, называются эквивалентными, если для всякого входного слова p ∈ X∗ выполняется λ(a, p) = λ′(b, p), где λ′ – функция выходов автомата A или B. С каждым состоянием a связывается автоматное отображение λ_a множества входных слов во множество выходных, определяемое равенством λ_a(p) = λ(a, p) для всех p ∈ X∗. Двойственным образом определяется множество μa всех вход–выходных слов автомата, оканчивающихся в состоянии a. Ограничение автоматного отображения на множество слов длины k обозначаем λ^k_a. Автомат называется приведенным, если все его состояния попарно неэквивалентны.

В дальнейшем будем рассматривать автоматы A и B, у которых входные и выходные алфавиты совпадают, то есть A = (A, X, Y, δ, λ) и B = (B, X, Y, δ, λ). В этом случае, как обычно, отображение φ: A → B будет называться гомоморфизмом автомата A в автомат B, если для любых a ∈ A и x ∈ X :

Пусть e = (a, x, y, b) – дуга автомата A и e′(φ(a),x,yφ(b)) — дуга автомата B, т.е. гомоморфизм φ индуцирует некоторое отображение множества дуг E_A во множество дуг E_B. Это отображение будем также обозначать φ и писать φ(e) = e′. Дуга e′ называется образом дуги e по гомоморфизму φ, а дуга e называется прообразом e′ по φ.

Гомоморфизм φ называется полным, если каждая дуга из B имеет прообразом некоторую дугу из A. Полный взаимно однозначный гомоморфизм A на B называется изоморфизмом, автоматы A и B называем изоморфными и обозначаем A = B. Взаимно однозначный гомоморфизм может быть не полным, в этом случае будем говорить об изоморфном вложении автомата A в B и писать A ⊆ B. Как обычно,изоморфизм A на себя называем автоморфизмом.

Пусть A = (A,X, Y, δ, λ) – приведенный автомат и e = (s, x′, y′, s1) – его дуга. Под переброской дуги e, например, в состояние s2 будем понимать замену этой дуги на дугу (s, x′, y′, s2). При s1 ≠ s2 переброску назовём нетривиальной. Далее, если не оговорено противное, рассматриваются нетривиальные переброски. Пусть автомат A′ получен из автомата A переброской некоторого множества дуг M ⊆ Ea, среди которых хотя бы одна переброска нетривиальная (такие множества перебросок также называем нетривиальными). Задача заключается в том, чтобы определить условия, при которых автомат A′ остается изоморфным исходному автомату A.

Пример сохранения поведения.

Легко привести примеры, когда результатом переброски в автомате двух дуг является новый автомат, не изоморфный исходному. Рассмотрим противоположный пример, когда переброска трёх дуг в приведенном автомате приводит к автомату, изоморфному заданному (см. рис.1).

Приведем пример, когда переброска трёх дуг в приведенном автомате также приводит к автомату, изоморфному заданному (см. рис.1). Автомат A′ является результатом переброски трёх дуг в автомате A: дуга (s, 0, 0, 11) перебрасывается в состояние 12, т.е. заменяется дугой (s, 0, 0, 12), дуга (t, 0, 0, 12) перебрасывается в состояние 13, т.е. заменяется дугой (t, 0, 0, 13), а дуга (u, 0, 0, 13) перебрасывается в состояние 11, т.е. заменяется дугой (u, 0, 0, 11). Легко видеть, что отображение φ: A→A′, такое, что: φ(1) = 1′; φ(2) = 3′; φ(3) = 4′; φ(4) = 2′; φ(5) = 6′; φ(6) = 7′; φ(7) = 5′; φ(8) = 9′; φ(9) = 10′; φ(10) = 8′; φ(s) = t′; φ(t) = u′; φ(u) = s′; φ(11) = 11′; φ(12) = 12′, φ(13) = 13′, реализует изоморфизм автомата A на автомат A′, т.е. автомат A′ также приведен и эквивалентен автомату A.

В [5] были сформулированы достаточные условия сохранения поведения авто- матом при переброске двух дуг, и было показано, что для любого натурального k > 1 существует приведенный автомат, в котором найдется подмножество из k дуг, одновременная переброска которых приводит к изоморфному автомату.

В настоящей работе основное внимание уделено получению необходимых условий, при которых возможна переброска дуг в общем случае. Более детально исследуются необходимые условия в случае переброски двух дуг.

Необходимые условия сохранения поведения.

В дальнейшем нам понадобятся понятия фрагмента автомата и идентификатора состояния, которые приведем, следуя [4]. Идентификатором состояния a автомата A (по поведению) называется такая пара множеств вход–выходных слов W_a = (V₁, V₂), что V₁ ⊆μ_a, V₂⊆ λ_a, и для любого другого состояния b ≠ a хотя бы одно из этих включений не выполняется.

Фрагментом автомата A называется всякий автомат R (в общем случае частичный), для которого существует гомоморфизм в A. Обозначим через R_u фрагмент автомата R с выделенным в этом фрагменте некоторым состоянием u. Используя понятие фрагмента, дадим более общее понятие идентификатора состояния автомата.

Фрагмент R_u называется идентификатором состояния a автомата A, если при любом гомоморфизме φ автомата R_u в автомат A выполняется равенство φ(u) = a.

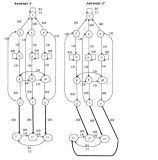
Рис. 1. Пример изоморфизма автоматов при переброске трёх дуг

В [4] показано, что каждому идентификатору состояния W_a по поведению (как паре множеств вход–выходных слов) можно поставить в соответствие фрагмент (частичный автомат), также являющийся идентификатором этого состояния. Такой идентификатор–фрагмент также будем называть идентификатором по поведению.

Можно привести пример, показывающий, что не каждый идентификатор–фрагмент является идентификатором по поведению. При исследовании отношения изоморфизма автоматов важными являются структурные свойства графа переходов автомата.

Назовём структурным идентификатором состояния a автомата A такой фрагмент R_u, изоморфно вкладываемый в A, что при любом изоморфном вложении R_u в A состояние u отображается в a. Множество всех идентификаторов (как структурных, так и по поведению), состояния a в автомате A обозначим I_u(A).

Пусть M – множество перебрасываемых дуг в A, M′ – множество переброшенных дуг в A′ и ˜M∪Mφ_-1(M′). Обозначим через Aм и A˜м частичные автоматы, полученные из A в результате удаления всех дуг из множеств A_M иA_˜м соответственно. Тогда справедливо

Утверждение 1. Если <→ изоморфизм A на A′, то → автоморфизм автомата A˜м.

Доказательство. Пусть → изоморфизм A на A′. Удалим из автомата A множество дуг φ(˜М)=φ(М)∪М′, а из A′ – множество образов этих дуг φ(˜М)=φ(М)∪М′. Получим соответственно автоматы А˜м и Аφ(˜м). В силу построения этих автоматов → является изоморфизмом А˜м на Аφ(˜м). Предположим, что X′′2d не является автоморфизмом. Тогда в А˜м существует дуга e = (a, x, y, b), образ которой в автомате Аφ(˜м) – дуга e′=(φ(a), x, y, φ(b)) отсутствует в А˜м. Но это значит, что дуга e′ есть результат переброски, а такие дуги были выброшены из A′. Полученное противоречие завершает доказательство утверждения 1.

Так как удаление дуг лишь сужает область определения функций δ и λ автомата A, то справедливо

Утверждение 2. Для любого состояния a из A справедливо I_s(A_M) ⊆ I_s(A).Примеры показывают, что для произвольного изоморфизма φ из A в A′ множества дуг M и φ_-1(М′) совпадают.

Далее предполагается, что М = φ_-1(М′). Тогда ˜М = М∪φ_-1(М′) и, значит, A_˜м = A_M.

Пусть φ — изоморфизм из утверждения 1 и для некоторых состояний s, t <∈ A, s≠t выполняется равенство φ(s) = t. Тогда справедлива

Лемма 1. Для любого фрагмента R_u такого, что существует гомоморфизм ψ фрагмента R_u в атомат A_M, при котором ψ(u) = s, найдётся такой гомоморфизм ψ′ фрагмента R_u в A_M, для которого ψ′(u) = t.

Действительно, так как ψ — гомоморфизм, а φ изоморфизм из утверждения 1, то ψ′=ψ°φ также гомоморфизм R_u в A_M, причём ψ′(u) = φ(ψ(u)) = t.

Из этой леммы следует, что R_u не является идентификатором ни состояния s, ни состояния t.

Следствие 1. Если φ — вышеуказанный изоморфизм, φ(s) = t и s≠t, то I_s(A_M) = I_t(A_M) = ∅.

По утверждению 1 φ — автоморфизм автомата A_M, а автоморфизм сохраняет идентификаторы. Поэтому I_s(A_M) = I_t(A_M), но ни один фрагмент Ru по лемме 1 не является идентификатором s в AM. Следовательно, I_s(A_M) = I_t(A_M) = ∅.

Наличие идентификаторов в автомате A_M позволяет определять те множества состояний автомата A, которые остаются неподвижными, т.е. переходят сами в себя, при любых изоморфизмах A в A′ (т.е. при всевозможных перебросках дуг из M, сохраняющих поведение A).

Множество M ⊆ E_A определяет автомат A_M и множество его автоморфизмов G_M. Множество G_M с операцией суперпозиции является группой, т.е. для любых φ,ψ∈G_M выполняется ψºφ ∈G_M и φ_-1∈G_M.

Теорема 1. Если автомат A′, полученный из A нетривиальной переброской дуг множества M, изоморфен A, то группа G_M нетривиальна.

Доказательство. Изоморфизм φ автомата A в A′ нетривиален в силу нетривиальности множества перебросок дуг из M, т.е. для некоторого состояния s φ(s) = s′, где s ≠ s′. По утверждению 1 φ – нетривиальный автоморфизм автомата Ам, и, значит, группа G_M также нетривиальна, так как содержит нетривиальную подгруппу, порождённую φ.

Заметим, что в группе G_M изоморфизмы автомата A в автоматы A′, получаемые всевозможными перебросками дуг из множестваM, определяют подмножество H_M⊆G_M автоморфизмов. Это множество Hм и порождает некоторую нетривиальную подгруппу группы G_M.

Укажем некоторые множества неподвижных точек, общие для всех автоморфизмов из группы G_M, а, значит, и для изоморфизмов автомата A во всевозможные автоматы A′.

Первое множество состояний определяется следствием 1. Во–первых, это множество A₁ тех состояний s∈A, для которых I_S(A_M)≠∅. Во–вторых, это множество всех состояний, которые достижимы из тех s ∈ A₁, для которых I_S(A_M)≠∅. Это следует из того, что при автоморфизме состояния, достижимые из неподвижных точек, также неподвижны относительно данного автоморфизма.

Второе множество составляют те состояния, для которых идентификаторами являются дуги из M.

При перебросках дуг для любого состояния s сохраняется множество λ^¹₁. Поэтому справедливо

Следствие 2. Если для любого s∈A выполняется λ^¹₁ ∈ I_S(A), то при любой переброске непустого множества дуг автоматы A и A′ не изоморфны.

Переброска двух дуг.

Пусть теперь автомат A′ является результатом переброски некоторых двух различных дуг в автомате A. Пусть, например, в автомате A′ дуга (s, x′, y′, s₁) заменена дугой (s, x′, y′, s₂), а дуга (t, x′′, y′′, t₁) заменена дугой (t, x′′, y′′, t₂).

Обозначим через ε отношение эквивалентности на множестве состояний A. Состояния a и b автомата A называются k-эквивалентными [4] , если для всякого входного слова p длины k выполняется равенство λ(a, p) = λ(b, p). Отношение k-эквивалентности обозначим через ε_k, а класс k-эквивалентности, содержащий некоторое состояние r, - через ε_k(r). Если k - минимальная длина такого слова p, для которого λ(a, p) ≠λ(b, p), то состояния a и b автомата A называются k-различимыми.

Состояния автомата A′ будем помечать штрихом, а обозначения для функций переходов и выходов оставим без изменения. Одноименные состояния вида (r, r′) автоматов A и A′, соответственно, назовем двойственными состояниями. Пусть A и A′ изоморфны, а n — множество состояний автомата A.

При доказательстве последующих утверждений будем пользоваться приёмом построения P_k – таблиц [3] для автомата B = A∪A′, полученного приписыванием автомата A′ к автомату A. Из правил построения P_k – таблиц следует, что с ростом k каждый класс в таблице P_k будет состоять из пар двойственных состояний до тех пор, пока не распадётся хотя бы одна из пар (s, s′) или (t, t′). Отсюда вытекает

Лемма 2. Если (s, s′) ∈∈ εi и (t, t′)∈εi для некоторого i > 1, то для любого состояния r ≠ s, t выполняется (r, r′)∈ε_i.

Доказательство. Предположим противное. Построим P_k – таблицы для автомата В=A ∪A′ и рассмотрим как с ростом k = 1, 2, ... распадаются классы ε₁(s) и ε₁(t). Заметим, что в силу изоморфизма автоматов A′ и A, каждый класс в P_k — таблицах автомата B должен содержать чётное число состояний — одинаковое число штрихованных и нештрихованных состояний.

Так как значения функций выходов автоматов A и A′ одинаковы, то в таблице P1 каждый класс эквивалентности состоит из пар двойственных состояний. Отсюда (s, s′)∈ ε₁, (t, t′) ∈ ε₁, но в силу исходного предположения, (s, t) ∉ ε₁. По лемме 2 (r, r′) ∈ ε₁ для любого r ≠ s, t. Пара (s, s′) по любому x ≠x′ переходит в пару двойственных состояний, и только для x′ это не так, поскольку δ(s, x′) = s₁, а δ(s′, x′) = s^′₂. Поэтому пара (s, s′) распадется сразу после того, как распадется пара (s₁, s^′₂). Аналогичные рассуждения справедливы и для пары (t, t′). Так как A приведен, то состояния (s₁, s2) являются i-различимыми, а состояния (t1, t2) j-различимы для некоторых i и j, где 1 ≤ i ≤ n-1, 1 ≤ j ≤ n-1. При этом, возможно, что i = j.

Выберем l = min(i, j). Пусть для определённости l = i. Тогда (s, s′) ∈ε_i, (t, t′)∈ε_i и по лемме 2 (r, r′)∈ε_i для любого r ∈ A, т.е. в таблице Pi все классы, по–прежнему, состоят из пар двойственных состояний. При этом (s₁, ε_i) ∈ε_i, (s2, s^′₂) ∈ε_i, но (s₁, s2) ∉ε_i и, значит, (s₁, s^′₂)∉s^′₂. Рассмотрим как распадается класс ε_i(s) на следующем (i + 1)–ом шаге. В таблице Pi этот класс состоит из пары (s, s′) и, возможно, других пар вида (r, r′). Заметим, что каждая такая пара (r, r′) по любому x переходит опять в пару двойственных, а, значит, i–эквивалентных состояний, откуда следует, что (r, r′)∈ ε′2. Поскольку δ(s, x′) = s₁, δ(s′, x′) =s^′₂ и (s₁, s^′₂) ∉εi, то (s, s′)∉ε_i+1. Из построения P_i+1 таблицы следует, что класс состояний ε_i+1(s) содержит само s и, возможно, пары вида (r, r′). Но тогда этот класс содержит нечётное число состояний, а это значит, что A и A′ не изоморфны. Случай l = j рассматривается аналогично. Полученное противоречие доказывает лемму.

Поскольку при n = 2 состояния s и t не являются 1–эквивалентными, то из леммы 3 вытекает

Следствие 3. В автомате с двумя состояниями невозможно перебросить две дуги таким образом, чтобы полученный автомат был изоморфен исходному.

Доказательство. При доказательстве леммы 3 было показано, что существует такое i, 1 ≤ i ≤ n−1, что (s, s′)∉εi+. Отсюда (s, s′)∉ε. Аналогично, (t, t′)∉ε.

Лемма 5. Существует минимальное k > 1 такое, что состояния s, s′, t, t′ являются (k > 1)-эквивавлентными, (s, t)∉ε_k, (s, t′)∈ε_k, (s′, t)∈ε_k и для всех состояний r ≠ s, t справедливо (r, r′)∈ε_k.

Доказательство. Из леммы 4 следует, что существует минимальное k₁ такое, что (s, s′)∉ε_k1 или (t, t′)∉ε_k1, или одновременно (s, s′)∉ε_k1 и (t, t′)∉ε_k1. Так как (s, s′)∈ε_k1-1 и (t, t′)∈ε_k1-1, то по лемме 2 (r, r′)∈ε_k1-1 для любого r ∈ A. При этом каждая пара (r, r′), за исключением пар (s, s′) и (t, t′), по любому x опять переходит в пару двойственных состояний. Поэтому из построения P_k1 следует, что для всех состояний r ≠ s, t, справедливо (r, r′)∈ε_k1. С другой стороны, в силу приведенности автомата A, существует минимальное k₂, при котором (s, t)∉ε_k2.Покажем, что k₁ = k₂.

Предположим, что k₁ ≠ k₂. Рассмотрим два случая: kk₂ < k₁ и k₁ < k₂.

1. k₂ < k₁. Тогда (s, s′)∈εk2 и (t, t′)∈εk2, но (s, t)∉εk2. По вышесказанному, хотя бы одна из пар (s, s′) или (t, t′) k1–различима, и при этом (r, r′)∈εk1 для всех r ≠ s, t. Пусть для определенности (s, s′)∉εk1. Тогда в таблице Pk1 класс εk1(s) состоит из состояния s и, возможно, пар вида (r, r′), т.е. содержит нечётное число состояний. Но тогда автоматы A и A′ не изоморфны. Случай (t, t′)∉εk1 рассматривается аналогично.

2. k1 < k2. Пусть для определённости (s, s′)∉εk1 (случай (t, t′)∉εk1 аналогичен данному). Возможны следующие два случая:

a) (t, t′)∉ε_k1. Так как (s, s′)∉ε_k1-1 и (t, t′)∉ε_k1-1, то по лемме 2 все классы (k1−1)–эквивалентности состоят из пар двойственных состояний. Поскольку все пары (r, r′), отличные от (s, s′) и (t, t′), по всем x переходят опять в пары двойственных состояний, получаем, что (r, r′)∈ε_k1. Кроме того, (t, t′)∈ε_k1. Таким образом, в таблице Pk1 все состояния, кроме s и s′, входят в классы k1–эквивалентности попарно с двойственными им. Но тогда класс ε_k1(s), равно как и класс ε_k1(s′), содержат нечётное число состояний, откуда следует, что A и A′ не изоморфны;

б) (t, t′)∉ε_k1. Поскольку k1 < k2, то (s, t)∈ε_k1. Рассуждая аналогично п.а), приходим к выводу, что в таблице Pk1все состояния, отличные от s и t, входят в классы k1–эквивалентности двойственными парами. При этом пары (s′, t′) и (s, t) принадлежат разным классам k1–эквивалентности. Отсюда следует, что класс ε_k1(s) содержит нештрихованных состояний больше, чем штрихованных. Следовательно, A и A′ не изоморфны.

Полученное противоречие доказывает, что k₁ = k₂. Другими словами, пары состояний (s, t), (s, s′) и (t, t′) являются k–различимыми, где k = k₁ = k₂. Нетрудно видеть, что единственный способ разбиения класса k1–эквивалентности, содержащего s, s′, t, t′, не нарушающий изоморфизма A и A′, следующий: (s, t′)∈ε_k и (s′, t)∈ε_k. Лемма доказана

Теорема 2. Справедливы следующие утверждения:

1)на перебрасываемых дугах отметки входных символов совпадают: x′ = x′′, причём x′ есть начальная буква кратчайшего слова, различающего s и t;

2)на перебрасываемых дугах отметки выходных символов совпадают: y′ = y′′;

3)состояния s и t, из которых перебрасываются дуги, различны.

Доказательство. Докажем утверждение 1). По лемме 5 существует минимальное k такое, что класс (k – 1)—эквивалентности, содержащий s, s′, t, t′, разбивается в таблице P_k на два класса, содержащих, соответственно, пары (s, t′) и (t, s′). Пусть p = x₁x₂…x_k — слово минимальной длины k, различающее s и t. Обозначим u = δ(s, x₁) и v = δ(t, x₁). Так как x₁ — начальная буква кратчайшего слова, различающего s и t, то (u, v)∉ε_k-1. Покажем, что x1 = x′ = x′′.

Предположим противное. Возможны два случая: 1) x1 ≠ x′, x′′ и 2) x1 = x′ ≠ x′′ либо x1 = x′′ ≠ x′. Рассмотрим каждый из них.

Пусть x1 ≠ x′, x′′. В силу леммы 5 для всех i < k в таблице Pi любой класс состоит из пар вида (r, r′). Поэтому (u, u′)∈ε_k-1, (v, v′)∈ε_k-1. Учитывая, что (u, v)∉ε_k-1, получаем, что (u, v′)∉ε_k-1. Но тогда (s, t′)∉εk, что противоречит лемме 5.

Пусть теперь x1 = x′≠ x′′ или x1 = x′′ ≠ x′. Предположим для определённости, что x1 = x′ ≠ x′′. Тогда u = δ(s, x1) = δ(s, x′) = s1. По лемме 5 (s, t)∈ε_k-1, но (s, t)∉εk. По вышесказанному (u, v)∉ε_k-1, т.е. (s1, v)∉ε_k-1. При этом (s1, v)∈εk−2, так как в противном случае состояния s и t были бы (k — 1)—различимы. В силу леммы 5 состояния s1, s1′, v, v′ (k — 2)— эквивалентны, причем (s1, s1′)∈ε_k-1 и (v, v′)∈ε_k-1. Следовательно, (s1, v′)∉ε_k-1. Но тогда (s, t′)∉εk, что противоречит лемме 5. Случай x1 = x′′ ≠ x′ рассматривается аналогично.

Итак, в обоих случаях пришли к противоречию. Следовательно, x1 = x′ = x′′.

Докажем утверждение 2). По лемме 3 λ(s, x) = λ(t, x) для любого x ∈ X. По доказанному утверждению 1) x′ = x′′. Отсюда y′ = λ(s, x′) = λ(t, x′) = y′′.

Докажем утверждение 3). Из утверждений 1) и 2) следует, что обе перебрасываемые дуги должны иметь одну и ту же вход-выходную отметку. Поскольку из одного и того же состояния нельзя перебросить две различные дуги с одинаковыми вход-выходными отметками, то утверждение 3) справедливо. Теорема доказана.

Заключение.

Полученные необходимые условия сохранения автоматом поведения при перебросках дуг совместно с достаточными условиями из [5] дают определённый инструментарий, позволяющий исследовать поведение такого рода автоматов.

Условия допустимой переброски для двух дуг могут быть расширены на переброску 2_k дуг в случае, когда множество M может быть разбито на двухэлементные классы дуг, для каждого из которых независимо выполняются найденные условия.

Найденные структуры (рис.1) показывают, что переброски осуществляются для дуг, исходящих из состояний, лежащих вне сильно связных подавтоматов исходного автомата. При этом структура графа переходов обладает своего рода частичной симметрией, которая проявляется при удалении перебрасываемых дуг и описывается группой автоморфизмов, указанной в теореме 1.