Работа посвящена решению автоматных уравнений. Приводятся примеры приложений, задачи в которых сводятся к решению автоматного уравнения.

Одной из фундаментальных задач теории дискретных систем является задача описания поведения компоненты, которая в композиции с заданной частью системы удовлетворяет спецификации. Проблема формализуется как решение уравнения A @ X∼S [1,2], где X – интересующая нас компонента, контекст A описывает поведение известной части системы, S – спецификация, @ – операция композиции элементов, ∼ – отношение, в котором должны находиться система и ее спецификация. Особый интерес представляет решение уравнений в рамках теории математических машин, таких как конечные автоматы.

Конечные автоматы суть специальные словарные функции, отображающие последовательности в одном (входном) в последовательности в другом (выходном) алфавите, которые используются для описания поведения различных систем управления, таких как цифровые схемы, протоколы вычислительных систем и т.п. В данной работе мы рассматриваем ряд приложений, в которых возникает задача решения автоматного уравнения, показываем, каким образом можно решить автоматное уравнение, и кратко обсуждаем частные решения автоматных уравнений, которые представляют практический и/или теоретический интерес.

Конечные автоматы и языки

Конечным автоматом, или просто автоматом, называется пятерка A=(S, I, O, T, r), где S – конечное множество состояний с выделенным начальным состоянием r, I – входной алфавит, O – выходной алфавит и T⊆I×S×S×O – отношение переходов. Четверка (i,p,n,o)∈T описывает переход в автомате из состояния p в состояние n под действием входного символа i c выходным символом o. В общем случае в текущем состоянии для данного входного символа может существовать более одного перехода. Если для каждой пары (i,p)∈I×S есть хотя бы один переход, то автомат называется полностью определенным. В противном случае автомат называется частично определенным, или частичным. В частичном автомате можно выделить наибольший полностью определенный подавтомат, последовательно удаляя состояния, в которых не определен хотя бы один переход. Мы далее рассматриваем полностью определенные автоматы, если только явно не утверждается обратное. Автомат называется детерминированным, если для любой пары (i,p)∈I×S существует не более одной пары (n,o)∈S×O такой, что (i,p,n,o)<∈T [3]. В противном случае автомат называется недетерминированным.

Отношение переходов обычным образом распространяется на последовательности в алфавитах I и O. Языком, или поведением, автомата A в состоянии s, обозначение: L_A(s), называется множество последовательностей входо-выходных пар в алфавите I×O, получаемых при последовательных переходах из состояния s. Формально язык L_A(s) есть подмножество (I×O)∗, и последовательность (i₁O₁)…(i_kO_k)∈L_A(s), если и только если &exists;n∈S(i₁…i_k,s,n,O₁…O_k)∈T. Язык L_A(r) автомата в начальном состоянии r называется языком автомата A и обозначается L_A.

Состояние q недетерминированного автомата B = (Q, I, O, T′, q₀) называется редукцией состояния s недетерминированного автомата A = (S, I, O, T, s₀) (обозначение q ≤ s), если и L_B(q) ⊆ L_A(s). Состояния q и s называются эквивалентными (обозначение q ≅ s), если q есть редукция s и s есть редукция q. В противном случае состояния q и s не являются эквивалентными.

Автомат B = (Q, I, O, T′, q₀) есть редукция автомата A = (S, I, O, T , s₀), если L_B(q)⊆L_A. Если L_B=L_A, то автоматы A и B называются эквивалентными. Для детерминированных полностью определенных автоматов отношения редукции и эквивалентности совпадают.

Автомат, который не имеет эквивалентных состояний, называется приведенным. Известно [4], что для каждого автомата A существует эквивалентный приведенный автомат, который называется приведенной формой автомата A. Более того, для каждого недетерминированного автомата также есть эквивалентный наблюдаемый автомат (S, I, O, T, r), в котором для любой тройки (i,p,o)∈I×S×O существует не более одного состояния n<∈S такого, что (i,p,n,o)∈T.

Синхронная композиция конечных автоматов

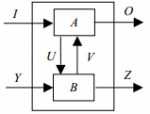
Рассмотрим композицию автоматов A и B на рис. 1. Автомат A имеет входной алфавит I×V и выходной алфавит U×O; автомат B имеет входной алфавит Y×U и выходной алфавит V×Z. Таким образом, язык автомата A есть LA⊆(I×V×U×O)∗, язык автомата B есть LB⊆((Y×U×V×Z)∗. Синхронная композиция или просто композиция A•B автоматов A и B имеет входной алфавит I×Y и выходной алфавит O×Z. Входо–выходной символ (iyoz)∈I×Y×O×Z принадлежит языку композиции, если и только если существует согласованная пара внутренних символов uv ∈ U×V таких, что (ivuo)∈L_A и (yuvz)∈L_B.

>

Рис. 1. Композиция автоматов

Синхронная композиция автоматов строится следующим образом. Сначала язык автомата A расширяется на множество Y×Z и язык автомата B расширяется на множество I×O посредством добавления на каждом переходе всех возможных пар из алфавита расширения. Полученные языки пересекаются, и строится проекция пересечения на алфавит композиции I×Y×O×Z. Приведенный наблюдаемый автомат с полученным языком и называется композицией A•B автоматов A и B. Все операции над языками осуществляются на основе соответствующих источников [5]. В зависимости от автоматов композиция может быть детерминированным или недетерминированным, полностью определенным или частичным автоматом.

Композиция A•B автоматов A и B считается полностью определенной, если в любом состоянии для любого входного символа существует соответствующие внутренние символы; в противном случае композиция – частичный автомат. Композиция автоматов является недетерминированной, если в некотором состоянии существует входной символ, которому соответствуют несколько внутренних символов. По определению, синхронная композиция детерминированных и полностью определенных автоматов может быть частичным и недетерминированным автоматом. Однако если в каждой обратной связи есть автомат Мура, т.е. автомат, выход которого на каждом переходе зависит только от текущего состояния, известно, что синхронная композиция полностью определенных детерминированных автоматов будет полностью определенным и детерминированным автоматом.

Теорема 1. Композиция полностью определенных детерминированных автоматов, в каждой цепи обратной связи которой есть автомат Мура, является полностью определенным и детерминированным автоматом.

Решение автоматных уравнений

Пусть автомат A имеет входной алфавит I×V и выходной алфавит U×O. Рассмотрим автомат C с входным алфавитом I×Y и выходным алфавитом O×Z и выражение A•X <≅C. Выражение A•X≅C называется автоматным уравнением. Неизвестный автомат X с входным алфавитом Y×U и выходным алфавитом V×Z описывает множество автоматов, которые в композиции с автоматом A эквивалентны автомату C. Автомат A иногда называют контекстом, а автомат C – спецификацией.

Автомат B c входным алфавитом YxU и выходным алфавитом VxZ называется решением автоматного уравнения A•X ≅C, если A•B≅C. Решение M автоматного уравнения называется наибольшим, если любое решение есть его редукция, другими словами, поведение любого автомата, который служит решением уравнения, содержится в наибольшем решении. В работах [3, 6] показано, что разрешимое автоматное уравнение имеет наибольшее решение, которое в общем случае является недетерминированным автоматом.

Решение автоматного уравнения сводится к решению уравнений в алгебре регулярных языков посредством соответствующих операций над источниками [5]. Язык автомата A расширяется на множество Y×Z, а дополнение языка автомата C расширяется на множество U×V. Полученные языки пересекаются, и строится дополнение проекции пересечения на алфавит композиции Y×U×V×Z. Приведенный наблюдаемый автомат, язык которого есть наибольшее префикс замкнутое подмножество полученного языка, обозначается M_L. Автомат M_L – наибольшее решение автоматного неравенства A • X≤C.

Справедлива следующая теорема:

Теорема 2. Уравнение A • X≅C разрешимо, если и только если A • M_L≅C. Если уравнение разрешимо, то всякое решение уравнения есть редукция автомата M_L. Однако не каждая даже полностью определенная редукция автомата M есть решение уравнения.

Частные решения автоматного уравнения

Практический интерес представляют не все решения автоматного уравнения. Например, особо интересны полностью определенные решения, поскольку поведение реальных систем обычно является полностью определенным. С другой стороны, решение должно быть таким, чтобы его композиция с автоматом A не имела тупиковых состояний и осцилляции, т.е. интерес представляют живые и безопасные решения.

Полностью определенные решения автоматных уравнений

Рассмотрим автоматное уравнение A•X≅C. Если наибольшее решение уравнения M_L – частичный автомат, то мы находим его наибольший полностью определенный подавтомат, последовательно удаляя состояния, в которых не определен хотя бы один переход. Если удаляется начальное состояние, то уравнение не имеет полностью определенного решения. Иначе мы получаем полностью определенный автомат, среди полностью определенных редукций которого содержатся все решения уравнения. Согласно теореме 2, в общем случае не все полностью определенные редукции служат решениями уравнения. Задача полной характеризации всех решений автоматного уравнения остается не решенной. Однако если редукция B автомата M_L – автомат Мура, то B есть решение уравнения.

Теорема 3. Если автомат M_L есть наибольшее решение уравнения A • X ≅ C, в котором A и C - полностью определенные и детерминированные автоматы и полностью определенная редукция B автомата M_L является автоматом Мура, то B есть решение уравнения.

Живые решения автоматных уравнений

Решение автоматного уравнения A • X≅C называется живым, если в композиции решения с автоматом A отсутствуют тупиковые состояния. Известно [6,7], что если уравнение имеет живое решение, то существует наибольшее живое решение уравнения.

Возможны два подхода [7] к получению наибольшего живого решения. Первый подход заключается в удалении из наибольшего решения всех последовательностей, ведущих к тупикам в композиции с автоматом A. Второй подход заключается в расщеплении состояний наибольшего решения. В этом случае расщепленные состояния автомата представляют только «хорошие» или только «плохие» последовательности. В этом случае набольшее живое решение служит подавтоматом автомата с расщепленными состояниями.

Применение автоматных уравнений в различных приложениях

Известен ряд задач синтеза и анализа дискретных систем, которые сводятся к решению автоматных уравнений.

Оптимизация цифровых схем. Исторически автоматное уравнение впервые было использовано для решения задачи оптимальной реализации компонент цифровых схем. В этом случае предполагается, что все компоненты цифровой схемы, кроме одной, реализованы оптимально. Совместное поведение не оптимизируемых компонент описывается контекстным автоматом A; спецификацией C является описание эталонного поведения всей схемы. Из множества решений уравнения A • X≅C выбирается оптимальное (в смысле реализации) решение. Процедура выполняется до тех пор, пока хотя бы одна компонента допускает оптимизацию. Известно [1], что подобный подход для оптимизации элементов цифровых схем оказался достаточно эффективным.

Синтез дискретных систем. Дискретные системы часто представляют в виде сети из взаимодействующих подсистем. При этом возникает вопрос: если часть дискретной системы уже синтезирована, то как найти неизвестную часть такую, чтобы поведение всей системы удовлетворяло заданной спецификации [1, 8]. Если поведение каждой компоненты системы описано конечным автоматом, то для синтеза неизвестной части системы можно использовать автоматное уравнение A • X≅C, где контекстный автомат A описывает поведение известной части системы и автомат-спецификация C описывает требуемое поведение всей системы. В общем случае автоматы A и C могут быть произвольными автоматами, в том числе частичными и недетерминированными [2]. С использованием данной технологии можно синтезировать конверторы для согласования протоколов в вычислительных сетях [9], конечно-автоматные компенсаторы [10] и контроллеры [1]. Конечно-автоматный компенсатор строится для устаревших устройств управления (УУ), требования к которым изменились, и является добавкой к старому УУ такой, чтобы их композиция удовлетворяла новым требованиям. Данная задача может быть решена посредством автоматного уравнения X •УУ≅C, где C описывает новые требования к устройству управления. В общем случае новые требования могут описываться недетерминированным автоматом.

Тестирование и диагностика дискретных систем. При тестировании многокомпонентных дискретных систем тесты обычно строятся для каждой компоненты системы. При синтезе тестов для заданной компоненты совместное поведение всех остальных компонент можно описать автоматом A. Тогда все неисправности компоненты, не обнаружимые на внешних полюсах системы, описываются редукциями наибольшего решения уравнения A•X≅C, где C описывает эталонное поведение всей системы. Таким образом, наибольшее решение автоматного уравнения показывает, с какой точностью возможно тестирование интересующей нас компоненты [11].

Автоматные криптосистемы. В автоматных криптосистемах композиция автоматов может быть использована для получения криптограммы [12]. В случае, когда часть компонент сети служит секретным ключом, задача криптоанализа сводится к решению соответствующего автоматного уравнения.

Формирование выигрышной стратегии в теории игр. В теории игр автоматные уравнения могут быть использованы для нахождения выигрышной стратегии. В этом случае выигрышная стратегия в логической игре (если существует) определяется как множество входо-выходных последовательностей наибольшего решения автоматного уравнения [13].

Во всех рассмотренных приложениях желательно иметь общее решение автоматного уравнения, из которого известным образом можно получить наилучшее в некотором смысле частное решение. Таким общим решением является наибольшее решение автоматного уравнения.

В данной работе кратко описана проблема решения автоматных уравнений. Изложены частные решения автоматного уравнения, которые могут быть интересны с практической точки зрения. Дальнейшие усилия направлены на исследование свойств таких решений для различных приложений.

Список использованной литературы

1. Kam T., Villa T., Brayton R., Sangiovanni–Vincentelli A. Synthesis of Finite State Machines: Functional Optimization. – Boston: Kluwer Academic Publishers, 1997.
   
2. Wonham W. M. Supervision of DES. – http://www.control.utoronto.ca/DES, 1999.
3. Евтушенко Н. Решение уравнений в логическом синтезе / Н.Евтушенко, Т.Вилла, А.Петренко, Р.Брайтон, А.Санджованни–Винцентелли. – Томск: Спектр, 1999. – С. 27.
4. Starke P.H. Abstract automata. – N.Y.: American Elsevier Publishing Company, 1972.
5. Агибалов Г.П. Лекции по теории конечных автоматов / Г.П.Агибалов, А.М.Оранов. – Томск: Изд–во Томск. ун–та, 1984.
6. Yevtushenko N., Villa. T., Brayton R.K., Petrenko A., Sangiovanni–Vincentelli A. Solution of synchronous language equations for logic synthesis // Вестник ТГУ (Приложение). – 2002. – №1(11). – С. 132–137.
7. Вилла Т. Характеризация живых решений синхронного автоматного уравнения / Т.Вилла, Н.Евтушенко, С.Жарикова // Вестник ТГУ. – Сентябрь 2003. – № 278. – С. 129–133.
8. Kim J. and Newborn M.M. The specification of sequential machines with input restrictions // IRE Trans. on Electronic Computers. – December, 1972. – P. 1440–1443.
9. Kumar R., Nelvagal S., Marcus S.I. A Discrete Event Systems Approach for Protocol Conversion // P. 1–23.
10. Ветрова М.В. Разработка алгоритмов синтеза и тестирования конечно–автоматных компенсаторов: Дис. – канд. техн. наук / М.В. Ветрова. – Томск: ТГУ, 2004.
11. Petrenko A., Yevtushenko N., Bochmann G.v. Fault models for testing in context // Proceedings of the IFIP Joint Intern Conf. FORTE/PSTV. –1996. – P. 163–178.
12. Саломаа А. Криптография с открытым ключом: Пер. с англ / А. Саломаа. – М.: Мир, 1995.
13. Жарикова С. Представление выигрышных стратегий в логических играх с помощью конечных автоматов / С.Жарикова, Е.Ярошевич, Н.Евтушенко // Доклады Третьей Всероссийской конференции с международным участием «Новые информационные технологии в исследовании дискретных структур». – Томск: Спектр, 2000. – С. 199–204.