О ПОСТРОЕНИИ МИНИМАЛЬНЫХ ДЕТЕРМИНИРОВАННЫХ КОНЕЧНЫХ АВТОМАТОВ, РАСПОЗНАЮЩИХ ПРЕФИКСНЫЙ КОД ЗАДАННОЙ МОЩНОСТИ
Автор:И.Р. Акишев, М. Э. Дворкин
Источник: УДК 519.713+519.766 ПРИКЛАДНАЯ ДИСКРЕТНАЯ МАТЕМАТИКА
Прикладная теория автоматов №2(8) 2010
Автор:И.Р. Акишев, М. Э. Дворкин
Источник: УДК 519.713+519.766 ПРИКЛАДНАЯ ДИСКРЕТНАЯ МАТЕМАТИКА
Прикладная теория автоматов №2(8) 2010
Санкт–Петербургский государственный университет информационных технологий, механики и оптики, г. Санкт–Петербург, Россия
Рассматривается задача о построенни минимального по числу состояний детерминированного конечного автомата, который принимает произвольный префиксный код заданной мощности над алфавитом {0, 1}. Доказывается, что данная задача является эквивалентной задаче о поиске кратчайшей аддитивной цепочки, заканчивающейся числом n.
Ключевые слова: префиксный код, детерминированный конечный автомат, автомат Мура, аддитивная цепочка.
В настоящее время префиксные коды находят широкое применение в различных областях информационных технологий, таких, как обработка и передача информации [1], сжатие данных [2] и многих других. В связи с этим изучение их свойств, а также способов эффективного построения и распознавания префиксных кодов представляет большой интерес.
Один из наиболее простых и естественных подходов к распознаванию префиксных кодов основан на применении конечных автоматов. Имеется ряд статей [3,4], посвященных исследованию задачи минимизации числа состояний автомата, распознающего некоторый заданный префиксный язык.
В настоящей работе представлен способ генерации минимального (по числу состояний) конечного автомата, распознающего произвольный префиксный код заданной мощности, а также изучается зависимость минимального возможного числа состояний автомата от мощности распознаваемого кода n.
Исследование этой зависимости представляет большую значимость, так как она характеризует нижнюю оценку размера автомата, распознающего любой префиксный код заданной мощности. Практический интерес представляет также изучение структуры самих префиксных кодов, которые соответствуют минимальным автоматам, так как такие коды являются в некотором смысле оптимальными с точки зрения их распознавания посредством конечных автоматов.
В работе будут рассматриваться детерминированные конечные автоматы (ДКА), так как они в большей степени приспособлены для применения на практике (в отличие от недетерминированных). Также будут рассмотрены минимальные автоматы Мура (с выходными символами), которые (в отличие от ДКА) можно применять не для принятия отдельных слов кода, а для декодирования непрерывной цепочки из последовательных кодовых слов.
Перед тем как сформулировать решаемую задачу, введем некоторые определения.
Определение 1. Алфавитом ∑ называют некоторое непустое конечное множество символов.
В настоящей работе рассматривается случай, когда ∑ = {0, 1}.
Определение 2. Словом называют некоторую конечную (возможно, пустую) последовательность символов алфавита: w = <∑σ1σ2…σl∈∑*. Количество символов в слове (число l) называют длиной слова. Пустое слово принято обозначать ".
Определение 3. Языком L называют множество слов {wi}⊆∑*. Язык конечной мощности C = {w1,w2, . . . ,wn} называют кодом, а n = |C|— мощностью кода.
Определение 4. Слово w =σ1σ2…σl является префиксом слова w′ =σ1′σ2′…σl′ , если l≤l′ и σi=σi′ для всех i ≤ l.
Определение 5. Язык (код) C называют префиксным, если для всех w,w′∈C слово w не является префиксом w′.
В последнем определении присутствует некоторая путаница, так как подобный язык (код), по мнению авторов, логичнее было бы называть беспрефиксным. Однако, в силу исторических причин, принято использовать именно указанное название.
Определение 6. Детерминированным конечным автоматом называется пятерка (Q, ∑, δ, s, Fi), где:
—Q – конечное множество состояний;
—∑ – алфавит;
—δ : Q ×∑→Q – функция переходов;
—s ∈ Q – начальное состояние;
—F ⊆ Q – множество терминальных состояний.
Обработка слова w = sigma;1σ2…σl ДКА A происходит следующим образом. Сначала автомат A находится в стартовом состоянии s. Затем на каждом шаге обработки автомат считывает очередной символ σi слова w и переходит из своего текущего состояния q в состояние δ(q, σi). К моменту, когда все символы входного слова w обработаны, автомат находится в некотором состоянии p. Говорят, что автомат A принимает слово w, если p ∈ F, и не принимает в обратном случае.
Определение 7. Множество слов, которое принимает ДКА A, обозначается L(A) и называется языком, принимаемым автоматом A.
Определение 8. Язык L называется регулярным, если существует некоторый ДКА A, такой, что L(A) = L.
После того как были введены базовые определения, можно более строго сформулировать исследуемую задачу.
Имеется некоторое натуральное число n. Необходимо построить ДКА, принимающий некоторый префиксный код C, такой, что |C| = n, и имеющий при этом наименьшее возможное число состояний (|Q| → min).
Известно [5], что для каждого языка, принимаемого некоторым ДКА, существует минимальный (по числу состояний) ДКА, принимающий этот язык. Более того, такой минимальный ДКА единственный (с точностью до изоморфизма состояний).
Очевидно, что в качестве решения рассматриваемой задачи может выступать только ДКА, являющийся минимальным для языка, который он принимает. В противном случае к данному ДКА можно было бы применить алгоритм минимизации [5], получив таким образом новый ДКА с меньшим числом состояний, принимающий тот же язык, что и исходный.
По этой причине при построении оптимального ДКА представляется возможным использование свойств минимальных автоматов, наиболее важное из которых (в рамках данной задачи) связано с правыми контекстами.
Определение 9. Правым контекстом состояния q автомата A (обозначается Rq) называется язык всех слов, которые переводят этот автомат из состояния q в какоелибо терминальное состояние.
В частности, язык L(A) есть не что иное, как Rs, где s — стартовое состояние автомата A.
Вернемся к минимальным автоматам.
Лемма 1. Детерминированный конечный автомат A является минимальным для языка L(A) тогда и только тогда, когда все состояния этого автомата достижимы из начального и имеют различные правые контексты [5].
Объяснение данного свойства заключается в том, что если в ДКА есть два состояния q и q′, такие, что Rq = Rq′, то они эквивалентны (также говорят: неразличимы), и их можно объединить в одно. Если же некоторое состояние q недостижимо из s, то его можно удалить из автомата, и это никак не повлияет на язык L(A).
Определение 10. Тупиковым состоянием ДКА называют состояние d, такое, что Rd = ∅. (Иногда такое состояние также называют дьявольским.)
Лемма 2. Пусть детерминированный конечный автомат A — минимальный автомат, принимающий некоторый непустой язык. Этот язык является префиксным тогда и только тогда, когда в автомате A ровно одно терминальное состояние, причем все переходы из него ведут в тупиковое состояние.
Доказательство. Так как язык L(A) не пуст и содержит хотя бы одно слово u, то этому слову должно соответствовать некоторое терминальное состояние автомата f∈F. Рассмотрим правый контекст Rf. В него входит пустое слово <ε, поскольку состояние терминальное. Если в него входит любое другое слово w, то, по определению, слово uw также принимается автоматом, а значит, принадлежит языку L(A), как и слово u. Таким образом, язык L(A) содержит два слова, одно из которых является префиксом другого. Следовательно, язык L(A) не префиксный, и имеет место противоречие.
Итак, правый контекст терминального состояния f состоит из единственного элемента – ε. Если в автомате A, помимо f, присутствует еще одно терминальное состояние f′, то для него также верно аналогичное рассуждение, а значит, Rf = Rf′ = {ε}. Таким образом, состояния f и f′ эквивалентны, а следовательно, автомат A не может быть минимальным, что противоречит условию теоремы. Это означает, что f – единственное терминальное состояние автомата A, а поскольку Rf = {ε}, то, находясь в состоянии f и считав любой очередной символ, автомат может перейти лишь в тупиковое состояние.
Докажем теперь обратное утверждение. Пусть минимальный ДКА A имеет ровно одно терминальное состояние f, а все переходы из него ведут в тупиковое состояние. Докажем, что язык L(A) является префиксным.
Предположим, что это не так – существуют некоторые неравные слова u и uw, принадлежащие L(A). Поскольку автомат принимает слово u, а терминальное состояние в автомате только одно, то по слову u из начального состояния автомат обязан переходить именно в состояние f.
Теперь рассмотрим поведение автомата в случае, когда он считывает слово uw, находясь в начальном состоянии. Обработав префикс u, автомат, как было показано выше, переходит в состояние f. Затем, считав первый символ непустого слова w, автомат перейдет в тупиковое состояние и навсегда останется там, считывая все оставшиеся символы слова w. Так как тупиковое состояние не является терминальным, то автомат A не примет слово uw. Получаем противоречие.
Итак, минимальный автомат, принимающий некоторый префиксный язык, имеет ровно одно терминальное состояние f. Более того, это состояние достижимо из любого другого состояния, кроме тупикового. Действительно, если существует состояние q, из которого не достижимо f, то Rq = ∅, а следовательно, q – тупиковое состояние.
Лемма 3. Пусть детерминированный конечный автомат A – минимальный автомат, принимающий конечный префиксный язык. Тогда в этом автомате нет циклов, кроме петель, ведущих из тупикового состояния в само себя.
Доказательство. Предположим, что в автомате A имеется цикл, проходящий через состояние q, отличное от тупикового. Рассмотрим символы, соответствующие переходам, образующим этот цикл. Эти символы образуют некоторое непустое слово v, которое переводит автомат из состояния q в него же.
Поскольку A минимальный, состояние q достижимо из начального по некоторому слову u (лемма 1). Кроме того, так как Rq ≠∅, то найдется некоторое слово w, переводящее автомат из q в терминальное состояние.
В таком случае языку L(A) принадлежат следующие слова: uw, uvw, uvvw и т. д. Получаем uv∗w⊆L(A). Следовательно, язык L(A) бесконечен, и имеет место противоречие.
Из леммы 3 следует, что искомый автомат A, после удаления из него тупикового состояния, будет представлять собой ациклический граф. Следовательно, его состояния можно отсортировать в порядке обратной топологической сортировки [6], то есть присвоить им такие последовательные номера, чтобы все переходы вели из состояния с большим номером в состояние с меньшим номером.
Пусть в ДКА A всего k состояний. Выпишем их все, кроме тупикового, в порядке присвоенных им номеров (использование нумерации с нуля будет оправданно далее):
q0, q1, q2, …, q(k−2).
Поскольку из любого состояния (кроме тупикового) достижимо терминальное, то оно будет находиться на первом месте в нашей последовательности (q0 = f). Аналогично, поскольку любое состояние достижимо из начального, то начальное состояние будет иметь наибольший номер (q(k−2) = s).
Рассмотрим теперь соответствующую последовательность мощностей правых контекстов для выписанных состояний:
a0, a1, a2, …, a(k−2),
где ai= |Rqi|. Из равенств Rq0 = Rf = {ε} следует, что a0 =1.
Рассмотрим некоторое нетерминальное состояние qi. Из него выходят два перехода, каждый из которых может вести либо в некоторое состояние с меньшим номером qj , либо в тупиковое состояние d.
Если оба перехода из qi ведут в d, то Rqi пуст, а следовательно qi – тоже тупиковое состояние, чего не может быть, так как рассматриваемый автомат A является минимальным.
Если один из переходов ведет в тупиковое состояние, а другой – в некоторое состояние qj (j < i), то мощность правого контекста qi равна мощности правого контекста qj (так как любому слову w ∈ Rqj взаимнооднозначно соответствует слово σw∈ Rqi , где σ — символ, которому соответствует переход из qi в qj).
Если оба перехода ведут в отличные от тупикового состояния qj и qk (j, k < i, возможно, j = k), то мощность правого контекста qi равна сумме мощностей правых контекстов состояний qj и qk.
Итак, рассматриваемая последовательность ai обладает следующими свойствами:
1) нулевой элемент последовательности равен единице;
2) каждый элемент, кроме нулевого, либо совпадает с некоторым предыдущим, либо является суммой двух (возможно, одинаковых) предыдущих элементов.
Определение 11. Будем называть последовательность чисел, обладающую данными свойствами, квазиаддитивной цепочкой. Длиной квазиаддитивной цепочки a0 = 1, a1, a2, …, ar будем называть число r.
Итак, длина полученной квазиаддитивной цепочки на два меньше числа состояний в искомом автомате (так ее элементы соответствуют всем состояниям, кроме тупикового). При этом мощность языка L(A), принимаемого автоматом, равна последнему элементу цепочки, соответствующему начальному состоянию.
Таким образом, мы доказали следующую лемму.
Лемма 4. Любому минимальному детерминированному конечному автомату A с k состояниями, принимающему префиксный код заданной мощности n, соответствует некоторая квазиаддитивная цепочка длины k−2, заканчивающаяся заданным числом n.
Докажем теперь обратное утверждение.
Лемма 5. Любой квазиаддитивной цепочке длины k, оканчивающейся заданным числом n, соответствует некоторый детерминированный конечный автомат A с k + 2 состояниями, принимающий префиксный язык мощности n.
Доказательство. Проведем обратное построение, аналогичное рассмотренному выше. В качестве множества состояний Q автомата A возьмем множество {d, q0, q1, …, qk} мощности k + 2. Состояние qk = s сделаем стартовым, q0 = t– единственным терминальным, а d–тупиковым. Функцию переходов <δ для состояний q1, …, qk определим следующим образом:
– если в квазиаддитивной последовательности ai получалось повторением aj (j < i), то переходы из вершины qi будут вести в вершины qj и d;
– если же ai получалось как сумма aj и ak (j, k < i), то переходы из вершины qi будут вести в qj и qk.
Соответствие символов и переходов из заданной вершины можно выбрать произвольным образом.
Все переходы из состояний t и d направим в состояние d.
Так как из каждого из состояний q1,…, qk в полученном автомате A как минимум один из переходов ведет в нетупиковое состояние с меньшим номером, то очевидно, что по таким переходам из стартового состояния достижимо терминальное. Следовательно, язык L(A) содержит хотя бы одно слово и не является пустым.
Построенный автомат A, возможно, является неминимальным. Тогда применим к нему процедуру минимизации [5], получив новый автомат A′. Так как в процессе минимизации автомата возможно лишь удаление некоторых состояний, но не появление новых, то автомат A′ будет по-прежнему содержать единственное терминальное состояние t′, все переходы из которого будут вести в тупиковое состояние d′. Следовательно, по лемме 2, язык L(A′) = L(A)′префиксный.
Нетрудно также убедиться (с помощью индукции, аналогичной примененной при доказательстве леммы 4), что в автомате A выполнено равенство |Rqi|=ai, а значит, |L(A)| = |Rs| = |Rqk | = ak = n.
Из лемм 4 и 5 следует эквивалентность задачи нахождения минимальной квазиаддитивной цепочки с заданным последним числом и минимального конечного автомата, принимающего префиксный код заданной мощности.
Заметим один важный факт: кратчайшая квазиаддитивная цепочка, заканчивающаяся заданным числом, не может содержать одно и то же число несколько раз. В противном случае мы можем удалить из нее все вхождения повторяющегося числа, кроме самого первого, уменьшив тем самым ее длину. (При этом, если удаляемые вхождения использовались для получения последующих элементов цепочки, мы сможем использовать вместо них первое вхождение, не нарушив тем самым структуру оставшейся цепочки.)
Следовательно, в кратчайшей квазиаддитивной цепочке всегда имеет смысл получать очередной элемент лишь как сумму двух предыдущих.
Определение 12. Квазиаддитивная цепочка, в которой каждый элемент равен сумме двух предыдущих, называется аддитивной цепочкой.
Итак, кратчайшая квазиаддитивная цепочка, заканчивающаяся заданным числом, всегда является аддитивной.
Из этого наблюдения следует еще одно свойство искомого минимального ДКА.
Лемма 6. В детерминированном конечном автомате, принимающем некоторый префиксный код заданной мощности n и имеющем минимальное число состояний, нет переходов в тупиковое состояние, кроме как из единственного терминального и из тупикового состояний.
Доказательство. Предположим, что в автомате A имеется переход в тупиковое состояние из вершины qi, не являющейся ни терминальной, ни тупиковой. Как было установлено ранее в процессе доказательства леммы 4, из qi может вести лишь один такой переход. Значит, в соответствующей квазиаддитивной цепочке число ai получено путем повторения предыдущего элемента (соответствующего состоянию, в которое ведет второй переход из qi). Но наличие повторений в цепочке означает, что она неминимальна (повторное число можно удалить), а следовательно, автомат A имеет неминимальное число состояний.
Из того факта, что любая кратчайшая квазиаддитивная цепочка является аддитивной, а также из лемм 4 и 5 вытекает следующая важная теорема.
Теорема 1. Задача нахождения детерминированного конечного автомата A с минимальным числом состояний, принимающего некоторый префиксный код заданноймощности n, эквивалентна задаче построения кратчайшей аддитивной цепочки, заканчивающейся заданным числом n.
В качестве примера на рис. 1 приведен минимальный ДКА, принимающий префиксный код мощности 15. Он соответствует кратчайшей аддитивной цепочке, заканчивающейся числом 15: (1, 2, 3, 6, 12, 15).
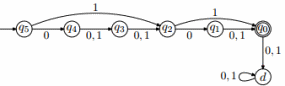
Рис. 1. Минимальный ДКА, принимающий префиксный код мощности 15
Подытожим изученные свойства искомого минимального ДКА. В автомате присутствует единственное терминальное состояние t, переходы из которого ведут в единственное тупиковое состояние d. Если удалить из автомата состояние d, то получится ациклический ориентированный граф, из каждой вершины которого (кроме t) выходитm ровно два ребра.
Задача о нахождении кратчайшей аддитивной цепочки является классической задачей дискретной математики [7]. Наиболее известным ее применением является задача об оптимальном алгоритме возведения произвольного числа в заданную степень, что немаловажно для криптографии [8].
Действительно, в процессе вычисления для данного числа x числа xn будут получены различные степени числа x, причем каждая следующая степень xk получается как произведение уже вычисленных степеней x=i и x=j , то есть x=k = x=i ·x=j = x=(i+j) . Поэтому показатели вычисляемых степеней составляют аддитивную цепочку, заканчивающуюся числом n. И минимизация длины такой аддитивной цепочки соответствует минимизации числа умножений при возведении в n-ю степень.
Классический бинарный метод возведения в степень [7] использует следующие соотношения:
Например, для возведения в 15-ю степень данный метод предлагает вычислить последовательность x^1, x^2, x^3, x^6, x7, x^14, x^15, что соответствует аддитивной цепочке (1, 2, 3, 6, 7, 14, 15).
Этот метод позволяет возводить в n-ю степень с помощью O(log n) операций умножения. Поскольку всякое число в аддитивной цепочке не превосходит максимального из предыдущих чисел, умноженного на два, аддитивная цепочка растет не быстрее, чем последовательность степеней двойки. Поэтому получить число n за o(log n) операций умножения невозможно, следовательно, бинарный метод возведения в степень является асимптотически оптимальным.
В то же время получаемая аддитивная цепочка не всегда является кратчайшей из возможных. Так, при n = 15 существует более короткая аддитивная цепочка (1, 2, 3, 6, 12, 15). (Здесь используется тот факт, что 15 = 3 · 5 - число 15 получается из тройки, которая, в свою очередь, получается из единицы.)
Если искать кратчайшую (не асимптотически, а абсолютно) аддитивную цепочку, заканчивающуюся числом n, сложность задачи возрастает коренным образом. Полиномиального решения этой задачи на данный момент неизвестно. Активно применяются методы поиска приближенного ответа, в том числе ведутся исследования по применению генетических алгоритмов [9] и "муравьиных алгоритмов" [10].
Длина кратчайшей аддитивной цепочки, заканчивающейся числом n, обозначается l(n). Из анализа метода бинарного возведения в степень вытекает неравенство l(n)<=[log n]+v(n)-1, где v(n) - это число единиц в двоичной записи числа n. Более точные асимптотические оценки для l(n) были доказаны в работе [11]:
log(n) + log(v(n)) - 2,13<=l(n)<= log(n)+((log(n)(1 + o(1)))/(log(log(n))))
Достаточно полный обзор имеющихся результатов о кратчайших цепочках можно найти на портале [12].
В работе [13] показано, что задача нахождения кратчайшей аддитивной цепочки, которая содержит в качестве подпоследовательности данную последовательность b1, b2, . . . , bk, является NP-полной [5]. То есть естественное обобщение рассматриваемой задачи не имеет полиномиального решения, если P ≠ NP.
Рассмотрим теперь следующую задачу: пусть имеется некоторый поток символов, который является последовательностью слов заданного префиксного кода, следующих подряд друг за другом. Необходимо по мере чтения этого потока разбивать его на отдельные кодовые слова для дальнейшей обработки.
Классический детерминированный конечный автомат, описанный выше, не подходит для данной задачи, так как он умеет лишь принимать или не принимать некоторые конечные слова языка.
В данной же ситуации требуется такой автомат, который смог бы получать бесконечный входной поток и уведомлять о том, когда прочитано очередное кодовое слово и начинается новое.
Для этой цели удобно использовать автомат Мура, который является частным случаем автомата с выходными символами.
Определение 13. Автоматом Мура называют шестерку (Q, ∑, δ, s, ∧, μ), где
—Q – конечное множество состояний;
— ∑ – входной алфавит;
— ∧ – выходной алфавит;
— δ : Q × ∑→Q – функция переходов;
— s – начальное состояние;
Как следует из этого определения, у автомата Мура, в отличие от обычного детерминированного конечного автомата, отсутствуют терминальные состояния. Вместо них появляются выходные символы, которые задаются в каждом состоянии функцией μ. Автомат Мура обрабатывает бесконечный входной поток и выдает последовательность соответствующих выходных символов.
Приментильно к исследуемой в данной работе задаче выходной алфавит автомата Мура ∧ будет состоять из трех символов ⊖, ⊕ и ⊖.
Символ ⊖ соответствует начатому, но неоконченному процессу чтения кодового слова.
Символ ⊕ соответствует случаю, когда из входного потока только что было считано очередное кодовое слово или же еще не было обработано ни одного входного символа, и следующим шагом начнется чтение нового кодового слова. В частности, μ(s) = ⊕.
Символ ⊖ соответствует случаю, когда в процессе обработки очередного входного символа была получена последовательность, которая не может являться началом ни одного слова из языка. Это означает, что входной поток содержит ошибку и не может быть распознан и разбит на слова. Как только автомат Мура сгенерировал выходной символ ⊖, дальнейшее распознавание входного потока становится невозможно, и вне зависимости от последующих входных символов автомат будет всегда продолжать выдавать выходной символ ⊖. Будем по аналогии с ДКА называть состояние d, для которого μ(d) = ⊖, тупиковым. Все переходы из тупикового состояния будут вести в него же. Очевидно, что в автомате Мура достаточно одного такого состояния.
Пример автомата Мура, распознающего префиксный код {00, 10, 11}, показан на рис. 2. Для входной последовательности 10100011011 этот автомат сгенерирует следующую последовательность выходных символов: ⊕ ⊕⊕ ⊕⊕ ⊕⊕ ⊕⊕ ⊕⊖⊖.
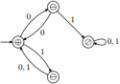
Рис. 2. Автомат Мура для кода {00, 10, 11}
Как и в случае с ДКА, поставленная задача – построить минимальный автомат Мура, принимающий некоторый префиксный код заданной мощности n.
Структуры минимального автомата Мура, распознающего поток слов некоторого префиксного кода (в описанном выше смысле), и минимального детерминированного конечного автомата, принимающего слова этого кода, взаимосвязаны – существует простой способ построить второй автомат на основе первого и наоборот.
Перед тем как описать такое построение, отметим следующее свойство минимального автомата Мура, распознающего префиксный код.
Лемма 7. В любом минимальном автомате Мура, распознающем некоторый префиксный код, существует ровно одно состояние q, такое, чтоμ(q) = ⊕, и это состояние – s.
Доказательство. Покажем, что такое состояние единственно. Пусть существует два различных состояния q и q′, таких, чтоμ(q) = μ(q′) = ⊕. Это означает, что находящийся в этих состояниях автомат только что принял очередное кодовое слово и готов начать считывать следующее. Однако начиная с каждого следующего кодового слова корректность цепочки входных символов никак не зависит от набора ранее принятых слов. Иными словами, для произвольной бесконечной цепочки символов w = σ1σ2…, подаваемой на вход автомату в состоянии q, всегда получится та же самая цепочка выходных символов, как и в случае, если бы на вход автомату подавалась цепочка w, когда тот находился в состоянии q′. Таким образом, эти состояния неразличимы автоматом, и, следовательно, можно удалить одно из них, например q′, перенаправив при этом все переходы, которые вели в него, в состояние q.
Однако так как μ(s) = ⊕, состояние s – это и есть искомое состояние.
Теорема 2. Пусть k – минимальное возможное число состояний для ДКА, принимающего префиксный код заданной мощности n. Тогда минимальное возможное число состояний автомата Мура, распознающего префиксный код мощности n, равно k–2, причем любому ДКА с k состояниями, принимающему некоторый префиксный код мощности n, взаимнооднозначно соответствует автомат Мура с k–2 состояниями, распознающий тот же самый код.
Доказательство. Рассмотрим минимальный ДКА, принимающий префиксный код мощности n и содержащий k состояний. Исключим из него тупиковое состояние d и единственное терминальное состояние t. Все переходы, которые раньше вели в t, направим в стартовое состояние s. Так как по лемме 6 в исходном ДКА в состояние d могли вести лишь переходы из удаленных состояний t и d, то все остальные переходы останутся корректно определены.
Назначим μ(s) = ⊕ и μ(q) = ⊖ для всех q≠s. Построенный таким образом автомат Мура будет содержать k–2 состояния. Нетрудно убедиться (по построению), что он будет распознавать тот же префиксный код, что и исходный ДКА.
Заметим, что в построенном таким образом автомате Мура будет отсутствовать тупиковое состояние.
Проведем теперь обратное построение. Рассмотрим некоторый минимальный автомат Мура, состоящий из k состояний (не считая тупикового, если оно в нем имеется) и распознающий слова префиксного кода заданной мощности n. По лемме 7 в нем есть всего одно состояние s, такое, что μ(s)= ⊕, и оно является стартовым. Введем новое состояние t, а также тупиковое состояние d, если оно отсутствовало в исходном автомате Мура. Все переходы, которые вели в состояние s, направим теперь в t, а все переходы из состояний t и d–в d.
Сделаем t единственным терминальным состоянием. Полученный ДКА будет иметь k+2 состояния и будет принимать тот же префиксный код, что и исходный.
Осталось показать, что при описанных выше построениях минимальному автомату будет ставиться в соответствие минимальный. Пусть имелся минимальный ДКА A, принимающий префиксный код длины n и содержащий k состояний. Применив описанное построение, получим автомат Мура B, состоящий из k–2 состояний. Предположим, что B не является минимальным. Тогда имеется некоторый автомат Мура B′, содержащий не более k–3 состояний и распознающий некоторый префиксный код длины n. Но из него можно построить ДКА A′, который будет содержать не более k–1 состояния. Следовательно, исходный автомат A не минимальный. Получаем противоречие.
Определение 14. Префиксный код C называется полным, если для любого слова v∈∑∗ существует слово w∈C, такое, что одно из них является префиксом другого.
Лемма 8. Префиксный код C заданной мощности, соответствующий автомату с минимальным числом состояний, является полным.
Доказательство. При доказательстве теоремы 2 было замечено, что у искомого
минимального автомата Мура отсутствует тупиковое состояние. Если подать на вход
автомату произвольное слово v∈∑∗, получится некоторая последовательность выходных символов, состоящая лишь из символов ⊕ и ⊖, причем начинается она с символа
На рис. 3 изображен минимальный автомат Мура, распознающий префиксный код длины 15, соответствующий ДКА, изображенному на рис. 1.
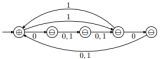
Рис. 3. Минимальный автомат Мура, принимающий префиксный код мощности 15
Выше была рассмотрена задача о построении минимального автомата, принимающего префиксный язык заданной конечной мощности.
Однако префиксные языки бывают как конечные, так и бесконечные. Если префиксный язык над конечным алфавитом бесконечен, то он представляет собой счетное множество. Для полноты исследования найдем минимальный по числу состояний ДКА, принимающий некоторый счетный префиксный язык.
Лемма 9. В детерминированном конечном автомате, принимающем счетный префиксный язык, не менее трех состояний.
Доказательство. Поскольку язык счетный и, следовательно, непустой, в ДКА должно быть хотя бы одно терминальное состояние, достижимое из начального. Назовем (любое) такое состояние t. Пусть оно достижимо из начального по слову u.
Рассмотрим Rt. В него входит пустое слово ε, поскольку t ∈F. Если в него входит еще хотя бы одно слово w, то языку L(A) принадлежат и слово u, и слово uw – язык L(A) не префиксный, имеем противоречие. Следовательно, правый контекст состояния t – это язык {ε}.
Следовательно, оба перехода из t должны вести в состояние с правым контекстом ∅, то есть в тупиковое состояние d, которое не совпадает с t.
Наконец, поскольку язык L(A) счетный, то правый контекст начального состояния не может равняться ни ∅, ни {ε}. Следовательно, начальное состояние не совпадает ни с t, ни с d, и доказано наличие в автомате A не менее трех состояний.
На рис. 4 приведен пример ДКА с тремя состояниями, принимающего счетный префиксный язык. Он принимает язык 0∗1–язык слов, состоящих из произвольного числа нулей и единицы в конце. Этот язык префиксный и имеет счетную мощность.
Рис. 4. ДКА, принимающий язык 0*1
Автомат Мура для этого языка имеет два состояния. Он приведен на рис. 5. Автомат Мура с одним состоянием не может принимать счетный язык: он будет либо
Рис. 5. Автомат Мура, принимающий язык 0*1
выдавать выходной символ ⊕ после каждого считанного символа, либо не будет выдавать его вовсе. В первом случае мощность языка равна двум, во втором–нулю.
Наконец, рассмотрим вырожденный случай – префиксный язык мощности ноль. Этот случай является особенным, поскольку в автомате, принимающем пустой язык, не требуется терминальное состояние. ДКА, принимающий (префиксный) язык мощности ноль, приведен на рис. 6. Автомат Мура для данного случая совпадает с ДКА; выходной символ в единственном его состоянии следует положить равным ⊗.
Рис. 6. ДКА, принимающий пустой язык
В данной работе рассмотрена задача о построении минимального автомата, принимающего произвольный префиксный код заданной мощности; доказана её эквивалентность задаче генерации кратчайшей аддитивной цепочки, заканчивающейся заданным числом.
Исследована также аналогичная задача для автоматов Мура.