Авторы: Jens Lienig
Название в оригинале: Physical Design of VLSI Circuits and the Application of Genetic Algorithms
Перевод: Фоменко Ф.С.
Источник (англ.):
Дрезденский технический университет Факультет электротехники и информационных технологий
Tanner Research, Inc. 2650 East Foothill Blvd. Pasadena, CA 91107
http://www.ifte.de/mitarbeiter/lienig/eabook.pdfЭлектронная автоматизация дизайна касается проектирования и производства систем VLSI. Один из важных шагов в создании кругооборота VLSI является своим физическим дизайном. Вход к физическому шагу дизайна является логическим представлением системы при дизайне. Продукция этого шага является расположением физического пакета, оптимально или почти оптимально понимающего логическое представление. Физические проблемы проектирования являются вообще комбинаторными в природе.
То, что делает электронные проблемы автоматизации дизайна особенно трудными по сравнению с традиционными комбинаторными проблемами оптимизации, то, что ряд элементов, который должен быть обработан, может быть довольно многочисленным - кругооборот может быть легко составлен из более чем одного миллиона ворот. Поэтому у практиков автоматизации дизайна есть устоявшаяся традиция быстрого рассмотрения и приспосабливания методов нового и альтернативного решения. Например, моделируемый отжиг является техникой оптимизации, подражающей отжигу кристаллов. Этот комбинаторный метод оптимизации был сначала предложен в литературе в 1983 и к следующему году, главные конференции по автоматизации дизайна имели многократные сессии на моделируемом отжиге для автоматизации дизайна [35]. Раннее принятие было снова повторено на нейронных сетях [36], которые моделируют принципы организации нервных систем.
Хотя автоматизация дизайна немедленно не добавляла генетические алгоритмы к своему основному ящику для инструментов, генетические алгоритмы последовательно использовались в области в течение прошлых десяти лет.
Цель этой статьи состоит в том, чтобы предоставить читателю актуальный краткий обзор генетических заявлений алгоритма на физический процесс проектирования VLSI. В Разделе 2, ниже, мы сначала кратко описываем физический процесс проектирования VLSI. Мы представляем систематический обзор генетических алгоритмов, успешно примененных к физическому процессу проектирования в Разделе 3. В Разделе 4 мы представляем параллельный генетический алгоритм для канала и проблемы направления распределительной коробки в кругооборотах VLSI. Мы завершаем с резюме в Разделе 5.
Главные шаги в типичном процессе проектирования VLSI показывают в рисунке 1. В частности подшаги физического дизайна даны.
Рис.1: процесс проектирования жареного картофеля VLSI
Физическая стадия проектирования является важной частью этого процесса. Его вход является вообще логическим описанием кругооборота, часто в форме netlist. Задача физического шага дизайна состоит в том, чтобы произвести расположение, назначение геометрических координат к компонентам кругооборота, или в самолете или в конкретном количестве плоских слоев. Расположение должно удовлетворить требования технологии фальсификации (достаточный интервал между компонентами кругооборота, и так далее) и должно минимизировать определенные критерии стоимости (длины взаимосвязей, и т.д.).
Из-за его сложности, физическая проблема расположения вообще разделена на подпроблемы, которые могут быть решены последовательно. Этими подпроблемами является все еще NP-hard, но они уменьшают практическую сложность до управляемого уровня. Физическая проблема проектирования обычно анализируется в следующие подпроблемы: разделение, размещение, направление и уплотнение.
Разделение является задачей деления кругооборота в меньшие части для сокращения проблемного размера. Кругооборот часто делится на части, осуществленные отдельно. Цель состоит в том, чтобы разделить кругооборот, таким образом, что размеры частей в пределах предписанных диапазонов и сложности взаимосвязи между этими частями минимизированы.
Размещение назначает клетки кругооборота к их геометрическим местоположениям на чипе. (Клетка может быть единственным транзистором, змеей или подкругооборотом, и т.д.), цель размещения зависит от стиля дизайна. В стандартном дизайне клетки (где все клетки имеют ту же самую ширину и помещены в ряды) и в макро-дизайне клетки (где клетки имеют различные размеры и помещены нерегулярно), цель состоит в том, чтобы минимизировать полную область расположения чипа. В матричном воротами дизайне (куда все клетки помещены в матричный образец) цель размещения состоит в том, чтобы гарантировать routability и минимизировать скопление взаимосвязей между клетками.
Направление следует за фазой размещения. Это определяет пути взаимосвязей между клетками, выложенными во время процедуры размещения. Цель состоит в том, чтобы соединить все булавки, принадлежащие той же самой сети согласно определенным качественным ограничениям (таким как уменьшение длин взаимосвязей, и так далее) и ограничения направления (взаимосвязи не должны срывать или пересекать друг друга, и т.д.).
Уплотнение часто является заключительным шагом в физическом дизайне расположения. Это преобразовывает символическое расположение (произведенный предыдущими шагами) в расположение маски, геометрические особенности маски на кремнии. Цель уплотнения состоит в том, чтобы минимизировать размер получающегося расположения кругооборота.
К нашему знанию первый основанный на развитии алгоритм для того, чтобы решить проблему разделения был издан в [37]. В отличие от предыдущих эвристических алгоритмов, обычно оптимизирующих только на одном ограничении, этот подход способен к обработке и много ограничений и много целей. Алгоритм, не включающий пересекающийся оператор, приводит к многоканальному разделению со справедливо уравновешенными размерами и небольшим количеством булавок для каждой части. Представленная стратегия имеет разумную скорость выполнения, которая подобна другим изданным эвристическим подходам.
В [21] и [22], различные кодирующие схемы проблемы разделения кругооборота исследованы для нахождения самого подходящего кодирования. Предложенный генетический алгоритм определенно скроен для разделения кругооборотов со сложными компонентами с разрядно-модульной структурой с помощью специального двухступенчатого кодирования разделения. Алгоритм состоит из перехода и оператора мутации и детерминированной стратегии улучшения.
Генетический алгоритм в [9] основан на структуре населения, вовлекающей поднаселение, имеющее их изолированное развитие, иногда прерываемое коммуникацией межнаселения. Хотя исследованные проблемы от фактических конструкторских разработок VLSI, сравнения с другими подходами и временем выполнения не представлены.
Гибридный генетический алгоритм для сокращенной отношением проблемы разделения представлен в [4]. Здесь проблема сформулирована с точки зрения гиперграфа. Генетическое кодирование является двойной последовательностью, где каждое подмножество компонентов кругооборота имеет соответствующее местоположение на последовательности. Прежде, чем генетический алгоритм выполнен, заказ этих генов определен глубиной, сначала ищут для улучшения исполнения генетического алгоритма. Традиционный переход и операторы мутации объединены с быстрым эвристическим разделением, относился к каждому потомку как к оператору улучшения. Исполнение алгоритма по сравнению с двумя другими подходами разделения, с помощью наборов исходных данных. Усредненный по всем точкам отсчета, представленный алгоритм достигает лучших результатов, чем другие подходы при наличии подобного количества времени выполнения для меньших графов и меньшего количества времени выполнения для самых больших графов.
Другой гибридный подход издан в [42]. Это объединяет моделируемый метод отжига с генетическим алгоритмом. Главное побуждение для этого подхода является parallelization моделируемой стратегии отжига путем замены ее единственного процесса поиска решения основанным на населении подходом с помощью генетического алгоритма. Два представленные эталонных результата не по сравнению с другими современными подходами.
Как упомянуто в Разделе 2, процедура размещения ответственна за назначение камер кругооборота к их местоположениям на чипе. Согласно изменению в размере и местоположении этих клеток, алгоритмы размещения могут быть разделены на алгоритмы для стандартного дизайна клетки, макро-дизайна клетки и матричного воротами дизайна.
После новаторской работы [6], дальнейших применений генетических алгоритмов [39],[40] и стратегии [24], [25] развития стандартного размещения клетки были представлены. Эти подходы производят высококачественные размещения реального мира - кругообороты VLSI, которые могут конкурировать со сложным моделируемым отжигом - базируемые стратегии размещения. Однако, изданное время выполнения не как конкурентоспособное (до 6 часов [24] и до 12 часов [40]).
В [33], время выполнения было уменьшено значительно при помощи параллельного внедрения генетического алгоритма, бегущего в распределенной сети автоматизированных рабочих мест. Общая численность населения расколота над различными процессорами, и механизм перемещения используется для обмена генетического материала между ними. В то время как результаты размещения подобны последовательному генетическому алгоритму, почти линейное ускорение может быть достигнуто с этим методом.
Мы затем обсуждаем три исследования, использующие генетические алгоритмы для макро-размещения клетки [5], [11], [12]. Подход в [5] основан на двумерном представлении битового массива макро-проблемы размещения клетки. Другая схема представления, двоичное дерево, применена в [11]. В [12], представлена комбинация генетического алгоритма с моделируемой основанной на отжиге стратегией оптимизации. Результаты эксперимента предполагают, что смешанная стратегия выступает лучше, чем чистый генетический алгоритм для макро-проблемы размещения клетки. Результаты лучше или сопоставимы с ранее изданными результатами точек отсчета размещения. Однако, время выполнения не так конкурентоспособно.
Применение генетического алгоритма для размещения матричного воротами дизайна было издано в [41]. Подход использует пакет Происхождения [19] в качестве основного генетического алгоритма. Этот пакет изменен со специальным алгоритмом для того, чтобы построить перестановки, который рассматривает только маленькое подмножество пространства решения. Результаты по сравнению с только одним ранее изданным алгоритмом. Время выполнения находится в заказе минут (до 1 часа).
<Направление является процессом соединения булавок, подвергающихся ряду ограничений направления. Направление VLSI обычно делится на глобальное направление (чтобы поручить сетям в определенные области направления) и детализированное направление (назначать сети на точные положения в области направления)./p>
Согласно положению булавок, детализированное направление может быть разделено на направление канала (булавки только расположены на двух параллельных сторонах области направления), и направление распределительной коробки (булавки помещены во все четыре стороны области направления).
Несколько работ были опубликованы, в котором генетические полученные из алгоритма стратегии применены к нерестриктивной проблеме направления канала [15],[17],[30],[32].
В [32], разрыв и перемаршрутизатор представлен, который основан на вероятностной отправке по неправильному адресу сетей одной структуры направления. Однако, направление сделано детерминированным алгоритмом Ли [27], и главные компоненты генетических алгоритмов, такие как переход различных людей, не применены. Результаты представлены только для одной точки отсчета направления канала. Никакое время выполнения для этого примера не дано.
Маршрутизатор в [15] объединения самый крутой метод спуска с особенностями генетических алгоритмов. Пересекающийся оператор ограничен обмену всеми сетями, и процедура мутации выполняет только создание новых людей. Представленные результаты ограничены простыми проблемами VLSI, и никакие замечания во время выполнения не сделаны.
Генетический алгоритм для направления канала, изданного в [30], основан на определенной для проблемы схеме представления, то есть люди закодированы в трехмерных хромосомах с представлением целого числа. Генетические операторы также определенно развиты для проблемы направления канала. Результаты или качественно подобны или лучше, чем лучшие изданные результаты для точек отсчета направления канала. Время выполнения алгоритма (в диапазоне 1... 50 минут), не так конкурентоспособно.
Алгоритмы в [15], [32] также применены к направлению распределительной коробки. В то время как маршрутизатор в [15] не годен к употреблению для больших точек отсчета направления распределительной коробки, алгоритм в [32] может конкурировать с другими алгоритмами направления распределительной коробки. Однако, время выполнения не дано.
Различный генетический алгоритм для направления распределительной коробки представлен в [31]. Подобный [30], генотип является по существу решеткой, соответствующей координационные пункты расположения. Переход и мутация выполнены с точки зрения сегментов взаимосвязи. Алгоритм предполагает, что распределительная коробка является растяжимой в обоих направлениях. Впоследствии, эти расширения уменьшены с целью достигнуть неподвижного размера распределительной коробки. В то время как более дорогостоящий во времени выполнения, на многочисленных эталонных примерах генетический алгоритм производит решения с равными или лучшими особенностями направления (netlength, число vias), чем ранее лучшие изданные результаты.
Как упомянуто в Разделе 2, уплотнение преобразовывает символическое расположение к расположению маски с целью уменьшения размера получающегося расположения кругооборота.
К лучшему из нашего знания единственное применение генетического алгоритма для уплотнения было продвинуто Fourman [14]. Он описывает два опытных образца генетических алгоритмов, выполняющих уплотнение символического расположения кругооборота. Хотя его результаты ограничены очень простыми структурами расположения, он действительно предлагает новое определенное для проблемы представление для дизайна расположения, включающего ограничения процесса уплотнения.
В следующем мы представляем параллельный генетический алгоритм для решения канала VLSI и проблем направления распределительной коробки с целью удовлетворяющих ограничений перекрестной связи для сетей. Этот подход является расширением [30], в котором последовательный генетический алгоритм был применен к проблемам направления канала. В [28] мы сначала ввели параллельный генетический подход и экстенсивно исследовали его главные параметры.
Как отмечалось ранее, направление взаимосвязи является одной из главных задач в физическом дизайне кругооборотов VLSI. Булавки, принадлежащие той же самой сети, связаны подвергающиеся ряду ограничений направления. Канал и направление распределительной коробки являются двумя наиболее распространенными проблемами направления в кругооборотах VLSI. Простые примеры проблемы направления канала и проблемы направления распределительной коробки показывают в рисунке 2.
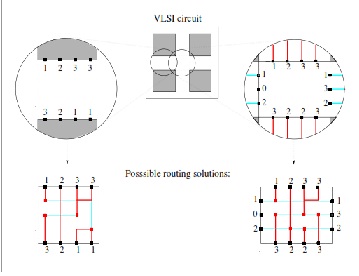
Рис. 2 – канал VLSI и распределительная коробка (право) проблема направления и возможные решения для направления.
Наши побуждения для того, чтобы развить параллельный генетический алгоритм для подробной проблемы направления были тройными. Во-первых, почти все ранее изданные подробные стратегии направления только рассматривают физические ограничения, такой как длина. Однако, с дальнейшей минимизацией в дизайне VLSI, новые электрические ограничения, такие как перекрестная связь, становятся доминирующими и должны быть обращены. Во-вторых, сегодняшняя типичная окружающая среда автоматизированного проектирования состоит из многих автоматизированных рабочих мест, связанных вместе быстродействующей местной сетью. Хотя много систем направления VLSI используют сеть для разделения файлов или баз данных дизайна, ни одна из известных программ направления (основанные на развитии или детерминированные алгоритмы) не использует этот распределенный компьютерный ресурс, чтобы найти что-либо подобное и ускорить их работу. В-третьих, все изданные генетические алгоритмы, рассматривающие проблему направления, являются последовательными подходами, то есть, одно население развивается посредством генетических операторов. Однако, недавние публикации (например [2], [26]) ясно указывают, что параллельные генетические алгоритмы с изолированным поднаселением развития (что обменные люди время от времени) выполняют заключающего пари, чем последовательные подходы.
Мы представляем параллельный генетический алгоритм для подробного направления, названного GAP (Генетический Алгоритм с Акцентированным равновесием), который бежит в распределенной сети автоматизированных рабочих мест. Наш подход считает качественные особенности направления таким как notlongth, число связей между слоями и важность перекрестной связи между соседними взаимосвязями. Из-за переменных факторов веса, эти цели направления могут быть легко приспособлены к требованиям данной технологии VLSI. Кроме того, на многих эталонных примерах, маршрутизатор приводит к результатам заключающего пари, чем лучший из ранее изданных.
Проблема направления VLSI определена следующим образом. Считайте прямоугольную область направления с булавками расположенной на двух параллельных границах (канал) или четырех границах (распределительная коробка) (см. рисунок 2). Булавки, принадлежащие той же самой чистой потребности, которая будет связана подвергающиеся определенным ограничениям и факторам качества. Взаимосвязи должны быть сделаны в границах области направления на символической области направления, состоящей из горизонтальных рядов и вертикальных колонок.
Мы определяем сегмент, чтобы быть непрерывной горизонтальной или вертикальной частью сети. (Таким образом любая связь между двумя булавками будет состоять из одного или более чистых сегментов.) Связь между двумя чистыми сегментами от различных слоев называют через. Полная продолжительность всех сегментов одной сети для соединения ее булавок определена как ее netlength.
В режимах подмикрона перекрестная связь происходит, главным образом, от двойной емкости между смежным (разбитая параллель) взаимосвязи. Чем короче длина этих параллель разбила сегменты, тем лучше исполнение кругооборота.
Таким образом следующие три фактора (которые должны быть минимизированы) используются в этой работе для оценки качества направления:
Различные пути существуют для нахождения что-либо подобное генетическому алгоритму [2]. Однако, большинство этих методов приводит только к ускорению алгоритма без качественных улучшений проблемных решений. Для получения лучших проблемных решений мы используем теорию акцентированного равновесия проектировать параллельный генетический алгоритм [7] , [10]. Генетический алгоритм с акцентированным равновесием является параллельным генетическим алгоритмом, в котором независимое поднаселение людей с их собственными функциями пригодности развивается в изоляции за исключением обмена людьми (перемещение), когда состояние равновесия всюду по всему поднаселению было достигнуто (см. рисунок 3). Предыдущее исследование показало генетические алгоритмы с таким акцентированным равновесием для имения превосходящей работы когда по сравнению с последовательными генетическими подходами [7], [9].
Различные пути существуют для нахождения что-либо подобное генетическому алгоритму [2]. Однако, большинство этих методов приводит только к ускорению алгоритма без качественных улучшений проблемных решений. Для получения лучших проблемных решений мы используем теорию акцентированного равновесия проектировать параллельный генетический алгоритм [7] , [10]. Генетический алгоритм с акцентированным равновесием является параллельным генетическим алгоритмом, в котором независимое поднаселение людей с их собственными функциями пригодности развивается в изоляции за исключением обмена людьми (перемещение), когда состояние равновесия всюду по всему поднаселению было достигнуто (см. рисунок 3). Предыдущее исследование показало генетические алгоритмы с таким акцентированным равновесием для имения превосходящей работы когда по сравнению с последовательными генетическими подходами [7], [9].
Генетический алгоритм, используемый каждым процессором и главным процессом, регулирующим параллельное выполнение, представлен в рисунке 5.
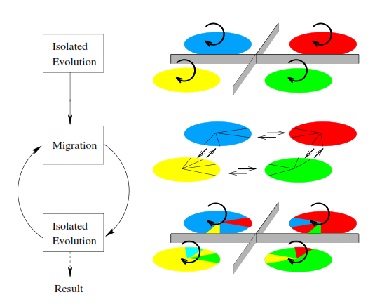
Рис. 3 – Акцентированная модель равновесия.
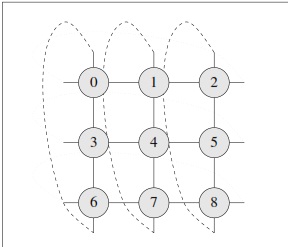
Рис. 4 – структура Соседства с девятью поднаселением.
Рис. 5 – краткий обзор Алгоритма.
Во-первых, главный процесс создает начальное поднаселение в каждом процессоре. Это начальное поднаселение состоит из беспорядочно построенного (то есть, не оптимизированный) решения для направления. Они разработаны случайной стратегией направления, соединяющей чистые пункты в произвольном заказе с беспорядочно помещенными взаимосвязями. (См. [30] для подробного описания нашей случайной стратегии направления.) Главный процесс состоит из данного числа эпох. Во время эпохи каждый процессор, disjointly и параллельно, выполняет последовательный генетический алгоритм на своем поднаселении для определенного числа поколений (длина эпохи). Впоследствии, каждый поднаселение обменивает определенное число людей (мигранты) с его четырьмя соседями. Процесс продолжает отдельное развитие каждого поднаселения во время следующей эпохи. В конце процесса существующий лучший человек составляет наше заключительное решение для направления.
Следующий раздел кратко описывает генетические операторы, используемые каждым процессором для развития его поднаселения.
Вычисление пригодности пригодность F (p) каждого € индивидуума p, Vc вычислен для оценки качества его взаимосвязей относительно остальной части поднаселения Vc-следующие факторы, принято во внимание (с различными весами) при определении F (p):
Выбор. Наша стратегия выбора, которая ответственна за выбор помощников для пересекающейся процедуры, является стохастическим осуществлением выборки с заменой [18] . Это означает любой индивидуальный ? пи, Vc отобран с вероятностью, пропорциональной ее ценности пригодности.
Переход. Во время перехода, два человека объединены для создания потомка. Наш пересекающийся оператор является пересекающимся оператором на 1 пункт [18], который дает высококачественные части направления помощников увеличенная вероятность того, чтобы быть переданным неповрежденный их потомку.
Переход выполнен с точки зрения проводных сегментов. Беспорядочно помещенная линия (crossline) перпендикуляр к краям области направления делит эту область на две секции, играя роль crosspoint. Эта линия может быть или горизонтально или вертикально помещена. Например, сегменты взаимосвязи исключительно на верхней стороне crossline унаследованы от первого родителя, и сегменты исключительно на более низкой стороне crossline унаследованы от второго родителя. Сегменты, пересекающие crossline, недавно созданы в пределах потомка посредством нашей случайной стратегии [30] направления.
Сокращение. Наша стратегия сокращения просто выбирает \VC\самых здоровых людей (Vc U Vnew) для выживания как Vc в следующее поколение.
Мутация оператор мутации выполняет случайные модификации на человеке (для преодоления местного optima) путем применения случайной стратегии [30] направления относительно беспорядочно отобранных взаимосвязей.
Мы представили систематический обзор генетических исследований алгоритма для физического процесса проектирования VLSI. Эти вклады вообще отличаются, чем стандартные генетические исследования алгоритма. Одно различие - то, что генетические операторы для физических алгоритмов дизайна являются как правило очень проблемой - определенный. Эта специфика происходит из-за чрезвычайной важности определения очень высококачественных решений - поэтому, компетентная информация о вероятной форме решений включена как можно больше. Комбинации генетических алгоритмов с другими стратегиями оптимизации больше не являются исключением. Как только “высококачественные области” идентифицированы генетическим алгоритмом, применение рутин локального поиска часто единственный способ гарантировать эффективное время выполнения. Другим различием является беспокойство о надежности. Там существует богатая коллекция точек отсчета автоматизации дизайна (например. [34]), и для метода решения, который будет принят, это должно быть продемонстрировано для работы последовательно хорошо над теми точками отсчета.
Мы также представили параллельный генетический алгоритм для канала и проблемы направления распределительной коробки. Наши результаты качественно подобны или лучше, чем самые известные следствия популярного канала и маршрутизаторов распределительной коробки. Кроме того, наш алгоритм в состоянии значительно уменьшить occurance перекрестной связи.
Генетические алгоритмы имеют очень большой потенциал в пределах физического дизайна кругооборотов VLSI. Проблемы, с которыми сталкиваются в этой области, чрезвычайно сложны, который является точно ситуацией, в которой исполнение генетического алгоритма сравнивается лучше всего с тем из других методов. Однако, генетический алгоритм базировался, подходы представляют практический интерес для сообщества VLSI, только если они конкурентоспособны с признанными существующими подходами относительно работы и времени выполнения. Эта глава дала обзор текущей ситуации в этой области с целью стимулировать и вести дальнейшие применения генетических алгоритмов.