Имитационная модель – распределенные алгоритмы Мерлина-Сигалла и Чанди-Мисры для вычисления таблиц маршрутизации
Автор: С.В. Грищенко, Савкова Д.Г.
Источник: Курсовой проект по распределенным системам, Донецк, ДонНТУ, 2013.
Автор: С.В. Грищенко, Савкова Д.Г.
Источник: Курсовой проект по распределенным системам, Донецк, ДонНТУ, 2013.
Грищенко С.В., Савкова Д.Г. Имитационная модель – распределенные алгоритмы Мерлина-Сигалла и Чанди-Мисры для вычисления таблиц маршрутизации. Выполнен анализ алгоритмов. Подготовлен программный аппарат тестирования, проведена сравнительная характеристика алгоритмов на крупной выборке синтетических тестов. Ключевые слова: таблица маршрутизации, граф, поиск маршрутов на графе, Мерлин-Сигалл, Чанди-Мисра.
Основной задачей данной системы является имитация построения таблицы маршрутизации для работы распределенной системы или компьютерной сети. Данная имитационная модель построена на основе MPI, что позволило произвести тестирование на эмуляторе кластера, т.е. на эмуляции максимально близкой к реальной задаче. Построение таблицы маршрутизации происходит по алгоритмам Мерлина-Сигалла и Чанди-Мисры.
Задача выполняется путем подробного логирования всех ключевых событий, которые происходят при поиске оптимальных маршрутов передачи информации.
Уравнение, определяющее значения d(u, v), которое можно использовать в алгоритмах поиска кратчайших путей
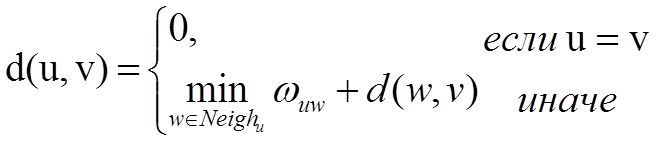
Рисунок 1 – Базовое уравнение алгоритмов
По этому уравнению можно определить кратчайшее расстояние между вершинами u и v.
Основные свойства уравнения, на которых основаны алгоритмы Мерлина-Сигалла и Чанди-Мисры:
Локальность данных означает, что для вычисления правой части уравнения нет необходимости в обмене данными между удаленными вершинами, т.к. в узле u требуется только локально-доступная информация или информация, которая имеется у соседей.
Независимость от вершин-адресатов предполагает, что для вычисления расстояния между любыми двумя вершинами требуется знать только расстояние между вершиной и ее соседями. Поэтому вычисление и анализ всех расстояний до заданной вершины-адресата можно проводить независимо от вычислений расстояний до других вершин сети.
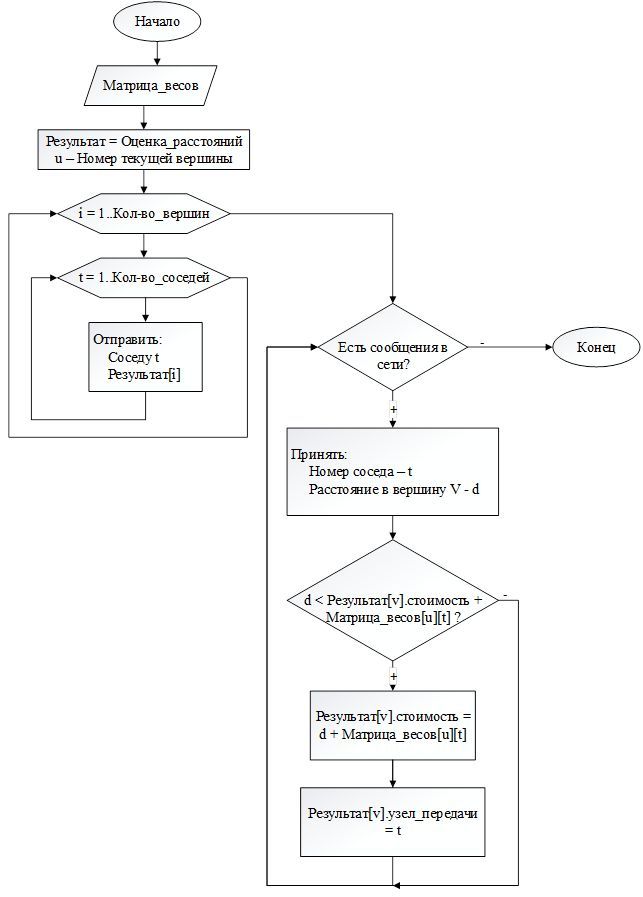
Рисунок 2 – Блок схема алгоритма Мерлина-Сигалла
Данный алгоритм вычисляет таблицы маршрутизации по отдельности для каждой вершины-адресата независимо друг от друга.
Для каждой вершины-адресата v алгоритм строит дерево с корнем в вершины v и проводит итеративное преобразование этого дерева, чтобы получить оптимальное входное дерево для вершины-адресата.
В каждую вершину u записывается оценка расстояния до вершины v и номер соседа, которому нужно передать пакет.
Каждый узел u отправляет свою оценку всем соседям, кроме того, через которого проходит маршрут.
Если узлом u получено сообщение от соседа с расстоянием d и обнаружено, что это расстояние в смме со стоимостью перехода к соседу меньше, чем текущая оценка, то значение текущей оценки полагается равным d плюс стоимость перехода к соседу, а значение вершины перехода - сосед, от которого было получено сооббщение.
Для вычисления всех кратчайших путей нужно совершить не более N-1 итераций. Кратчайшие пути ко всем вершинам-адресатам вычисляются за счет независимого применения предложенного алгоритма ко всем вершинам-адресатам.
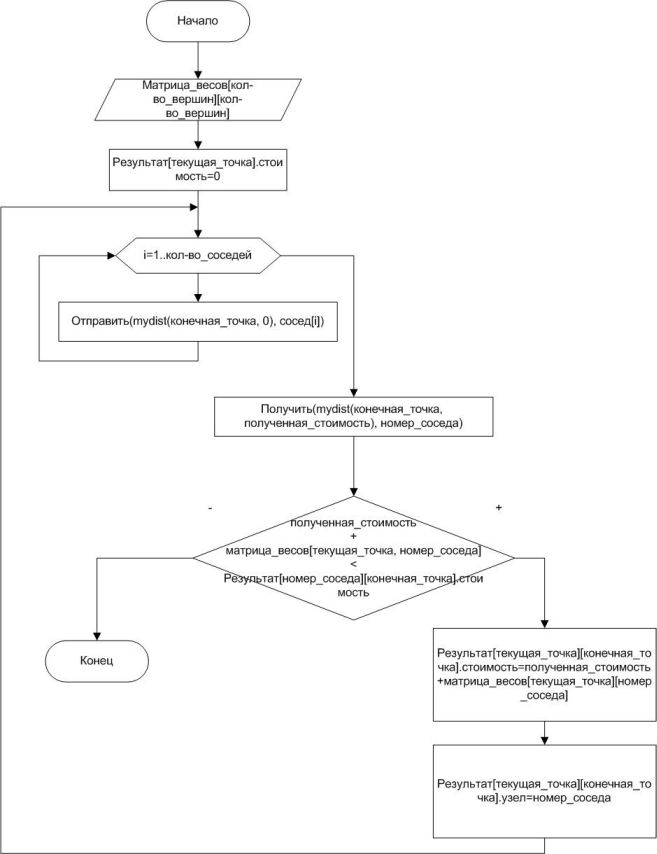
Рисунок 3 – Блок схема алгоритма Чанди-Мисры
Суть алгоритма заключается в том, что вычисление начинается в одной-единственной вершине-узле, другие узлы поочередно присоединяются к вычислению только после получения сообщения.
Для вычисления расстояния от каждой вершины до заданного узла v, каждый узел u устанавливает начальное значение оценки расстояния равным бесконечности. Узел v отправляет сообщение mydist(v,0) всем своим соседям. Вершина u, получив сообщение mydist(v,d) от соседа w проверяет - является ли d + стоимость перехода к соседу меньшей стоимость, чем теущая оценка перехода в вершине w, если да, то значением оценки становится полученная сумма и соседям отправляется mydist(v, d(u,v)).
Алгоритм Чанди-Мисры вычисляет таблицы маршрутизации по кратчайшим путям, совершая при этом обмен O(N*N) сообщениями и передавая O(N*N*W) битов информации по каждому каналу связи, имея, таким образом, коммуникационную сложность O(N*N*|E|) и битовую сложность O(N*N*|E|*W).
Программная система построена по принципу процедурного программирования. Использование ООП в программной системе не предполагается, т.к. библиотека MPI построена по процедурному принципу, а также в нашей работе важна скорость вычислений, затраты на которую увеличиваются при использовании объектно-ориентированного подхода.
Логически систему можно разбить на два основных модуля – модуль настройки системы и модуль имитационных вычислений.
Модуль настройки системы предполагает обработку ввода параметров работы системы, чтение входных данных, их рассылку всем процессам и установку системы в режим работы выбранного пользователем алгоритма. Данный модуль программы отвечает за взаимодействие с пользователем. Здесь присутствуют основные константы, определяющие режим работы программы, используемый алгоритм. Здесь также происходит проверка входных параметров и вывод информации об ошибках (если требуется).
Модуль имитационных вычислений в свою очередь разбит на два подмодуля, представляющих работу алгоритмов Мерлина-Сигалла и Чанди-Мисры. Данные алгоритмы предполагают выполнение некоторых однотипных задач, таких как подсчет количества соседей узла или вывод номера отработавшего процесса в лог. Решение подобных задач унифицировано при помощи отдельных функций. Данный модуль предоставляет прототип двух функций – для использования алгоритмов Мерлина-Сигалла и Чанди-Мисры соответственно. Эти прототипы являются интерфейсом взаимодействия данного модуля и модуля настройки системы, в котором в зависимости от выбранного пользователем алгоритма используется указатель на одну из функций модуля имитационных вычислений.
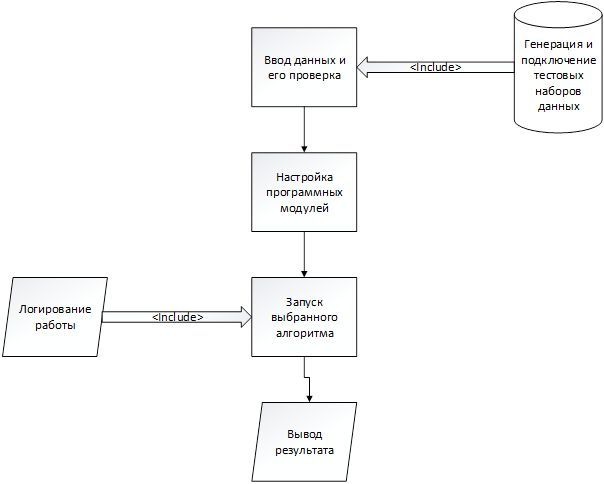
Рисунок 4 – Структура программной системы
На рисунке можно увидеть внешний модуль тестирования. Это отдельный программный комплекс, генерирующий тесты для имитационного анализа. Ему на вход подается количество узлов графа, количество связей между ними, а также максимально возможная стоимость перехода между вершинами. На выходе будет получен текстовый файл, описывающий структуру случайно сгенерированного графа, удовлетворяющего вышеуказанным входным данным. Таким образом для основной программной системы может быть сгенерировано достаточно обширное множество тестов.
Взаимодействие пользователя и программной системы происходит через командную строку.
Аргументами командной строки могут быть:
Для тестирования системы был разработан отдельный генератор графов.
На вход подается количество узлов графа, количество связей между ними, а также максимально возможная стоимость перехода между вершинами.
Цели экспериментов:
Посчитать производительность алгоритмов.
Показать графически зависимости между временем выполнения алгоритмов маршрутизации и размерности графа.
Определить лучший по производительности алгоритм.
Алгоритмы будут подвергаться экспериментам на графах от 1 до 50 точек.
На рисунке показан график зависимости времени выполнения алгоритмов от количества узлов для алгоритма Мерлина-Сигалла. Каждой линии на графике соответствует процессор. Процессоры завершали свою работу практически в одно и то же время. Причиной этому стало использование синхронных методов отправки/получения данных между процессорами.
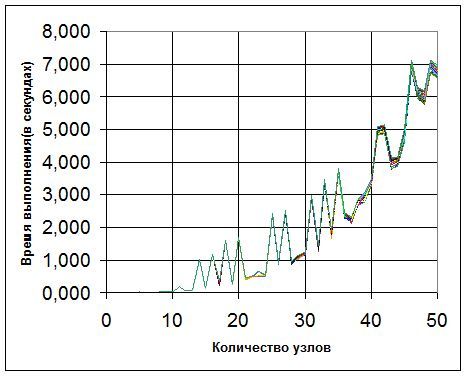
Рисунок 5 – Структура программной системы
На рисунке показан график зависимости времени выполнения алгоритмов от количества узлов для алгоритма Чанди-Мисры. Каждой линии на графике соответствует процессор. Как мы видим, между моментами окончания работы процессоров довольно большие промежутки времени. Это объясняется тем, что в реализации алгоритма использовались только асинхронные методы отправки и получения данных. Поэтому некоторым процессорам удается завершить свою работу намного раньше других и наоборот.
По графику наблюдается экспоненциальная зависимость между количеством узлов в графе и времени выполнения программы.
Резкие подъемы и спады на графике связаны с зависимостью времени выполнения работы от положения ребер на графе. Например, если в графе есть точки, у которых нет соседей, то они завершат свою работу сразу же, потому что им некому будет отправлять сообщения и не от кого получать. Т.к. графы в данном проекте генерировались случайным образом, отследить связность графа не представляется возможным на данном этапе разработки.
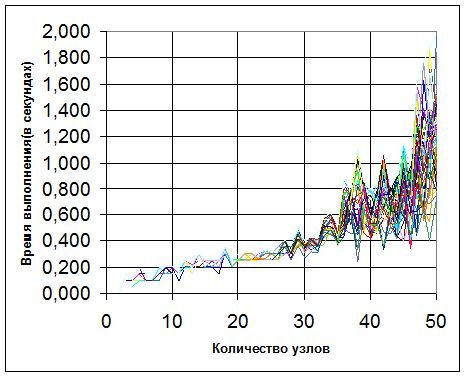
Рисунок 6 – Структура программной системы
На следующем графике показаны отличия в производительности алгоритмов Чанди-Мисры и Мерлина-Сигалла (рисунок 4.2). В качестве значений на оси Y выступало максимальное время работы процессоров.
Нельзя строго судить производительность по этим данным. Этому есть ряд причин:
1. Олифер В.Г. Олифер Н.А. Компьютерные сети. Принципы, технологии, протоколы: Учебник для вузов. 2-е изд. – Спб.: Питер, 2004. – 864с
2. Тель Ж. Введение в распределенные алгоритмы. – М.: МЦМНО, 2009. – 616с
3. В.П. Гергель. Теория и практика параллельных вычислений М:2007.