Герасимов И. Г., Привалов М. В. Моделирование процесса
прикрепления нейтрофилов крови in vitro с применением методов цифровой
обработки изображений
Оригинал: http://www.masters.donntu.ru/2008/kita/grinchenko/library/5.htm
Введение. В современной цитологии для решения диагностических и
лечебных задач необходима оценка комплекса параметров клеток. Однако в
настоящее время автоматизированные системы для выполнения такой оценки
фактически отсутствуют. В то же время получение оцифрованных изображений
проекций клеток и расчет их геометрических параметров не представляет
технических трудностей. К сожалению, работы начатые в этом направлении [1, 2,
3, 4] не получили развития в последнее десятилетие.
Постановка задачи. Одним из вопросов, ответ на который может позволить
повысить эффективность диагностики и лечения, является прогнозирование
процесса прикрепления, в частности, нейтрофилов, без чего они не в состоянии
выполнять свойственные им функции. Задачами данного прогнозирования являются
определение степени завершенности процесса и времени, необходимого для него.
Решение задач. На примере прикрепления нейтрофилов крови человека in
vitro предпринята попытка построения кинетической модели процесса, основанной
на расчете величин геометрических параметров клеток. Исследовали нейтрофилы
капиллярной крови человека в процессе их прикрепления к предметному стеклу при
комнатной температуре в течение времени (t) 60 мин. Путем микроскопирования и
оцифровки получены изображения нейтрофилов. На изображениях выделяли контур
нейтрофила, который представляли вектором точек с координатами (xi,
yi) и рассчитывали геометрические характеристики объекта: периметр
(P), площадь (S), компактность (C = P2/S), набор моментов первого (F1),
второго (F2) и третьего (F3) порядков, разность F3
- F1, а также интеграл множества нормированных дескрипторов Фурье
(FF) по [6]. Для повышения достоверности исследовали 10 контуров для каждого
изображения и рассчитывали среднее значение.
Получены зависимости каждого параметра от времени. Значения параметров,
использованные для построения зависимостей, приведены в табл. 1. Как видно из
таблицы, все параметры увеличиваются во времени, за исключением C и FF, которые
в пределах погрешности их расчета остаются постоянными.
Таблица 1. Геометрические параметры нейтрофила крови человека в процессе
прикрепления
Таблица 1.
Геометрические параметры нейтрофила крови человека в процессе прикрепления

Вид
зависимостей P и S от t (рисунок) позволил предположить, что полу-ченные кривые
могут быть описаны кинетическим уравнением первого порядка:
![]()
где c – P
или S в момент времени t;
b – P0 или S0 – соответственно P или S при t = 0;
a – (P∞ - P0) или (S∞ - S0) - P∞,
S∞ - соответственно P, S при t = ∞ ;
k – константа скорости процесса, c-1.
Получены параметры уравнения (1) для S и P (табл. 2). Величины коэф-фициентов
корреляции (r) указывает на то, что изменения P и S в процессе прикрепления
нейтрофилов действительно подчиняются кинетическому урав-нению первого порядка
(кривая на рисунке).
Таблица 2. Значения параметров уравнения

Как видно из
табл. 1 и, как можно было предположить, P и S изменяются с одинаковой скоростью
(ср. значения k для P и S). Поскольку скорость измене-ния P и S постоянна на
протяжении всего процесса, C также остается постоян-ной (табл. 1).
На основании значений k и погрешностей измерения P и S, задавая (P∞
- P0) < 2,5 пикселей и (S∞ - S0) <
100 пикселей, нашли t∞ - t, при котором процесс прикрепления
можно считать практически завершенным. Получили для P значение t∞
= 65 мин и для S - t∞ = 70 мин, что хорошо согласуется с
найденными значениями k (табл. 2). При этом P∞/P0 =
340/270 = 1,26, S∞/S0 = 7430/4600 = 1,62, что
хорошо согласуется с литературными данными.
Таким образом, полученная модель позволяет оценивать степень завер-шенности
процесса прикрепления нейтрофилов ограничиваясь временем ис-следования 20 – 25%
от t∞, то есть примерно 15 мин. и рассчитывая значения
интересующих параметров в любой момент времени.
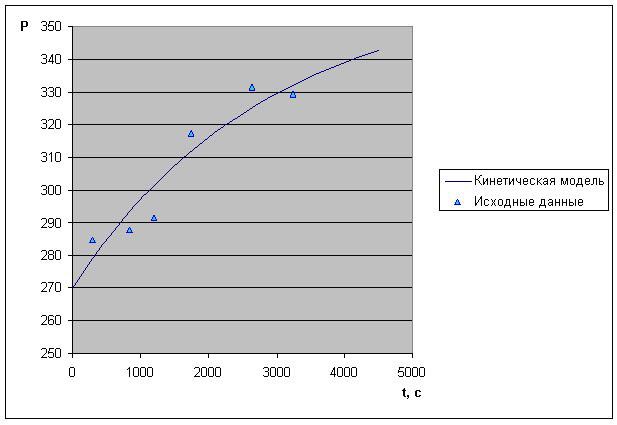
Рис. 1. Кинетическая модель изменения периметра нейтрофила в процессе
прикрепления.
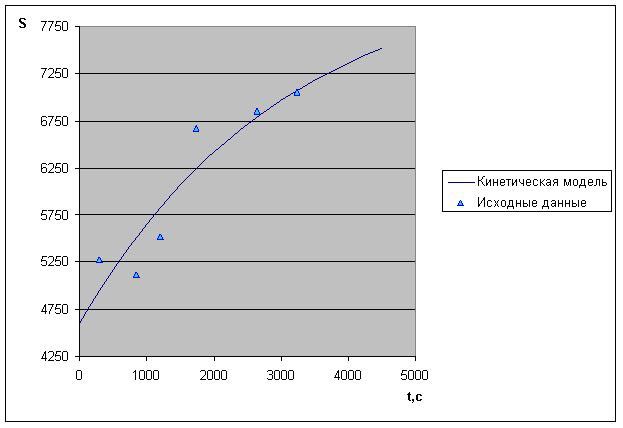
Рис. 1. Кинетическая модель изменения площади нейтрофила в процессе
прикрепления.
Выводы. На основании обработки изображений проекций клеток и
рас-чете их геометрических параметров получена модель процесса прикрепления
нейтрофилов крови человека in vitro, которая описана кинетическим уравнением
первого порядка. Найдены кинетические параметры уравнения и рассчитано время
завершения процесса прикрепления. Полученная модель по-зволяет существенно
уменьшить ввремя исследования для степени завершен-ности процесса прикрепления
нейтрофилов.
Для периметра и площади нейтрофила определены значения параметров модели и
обоснована ее адекватность реальному процессу прикрепления. По-строенная модель
позволяет определить стадию процесса прикрепления, а так-же момент времени его
завершения. Направлениями дальнейших исследований является построение моделей
для других геометрических параметров и уточне-ние моделей в их совокупности.
Библиографические
ссылки.
1. Медовый В.С., Балабуткин В.А., Верденская
Н.В., и др. Автоматизированные цитофотометрические тесты мазков крови для общей
клиники и скрининговых обследований населения. // Клин. лаб. диагн.. – 1997.
(10) – С6 - 8.
2. Погорелов В.М., Медовый В.С., Хазем Г.М., Козинец Г.И. Анализ клеточно-го
изображения. // Клин. лаб. диагн. – 1995. (3) – С 40 - 43.
3. Погорелов В.М., Медовый В.С., Балабуткин В.А., и др. 1997. Методы
ком-пьютерной цитологии в гематлогических исследованиях. // Клин. лаб. диагн. –
1997. (11)
– С 40 - 42.
4. Grenander U. 1997. Geometrics of knowledge. Proc. Natl. Acad. Sci. USA. –
1994. (3) – P 783 - 789.
5. Герасимов И. Г., Калуцкая О. А. Динамика некоторых параметров клеток
буккального эпителия в течение менструального цикла у женщин. // Цитология. –
1996. 38
(11) – С 1152 - 1157.
6. Shen L., Rangayyan R. M., Desautels J. E. L. Application of shape analysis
to mammographic calcifications // IFEE Transact. Med. Imag.- 1994.- V. 13, N 2.- P. 263- 274.
7. Попандопуло А. Г., Игнатов Д. Ю., Слипченко И. О., Васильев Р. Г., Меркулова
Е. Г., Герасимов И. Г. Влияние факторов культивирования на жизнеспособность
фетальных фибробластов человека in vitro // Вестн. неотложной и
восстановительной мед.- 2003.- Т. 4, N 2.- С. 323 - 325.