И.Ю. Василевский, И.Г. Сидоркина - Повышение точности функционирования элементов физических движков

Ключевые слова

Движок, визуальная реалистичность, аппроксимация, столкновение тел

Аннотация

В данной статье предложено описание метода расчета параметров столкновения тел, повышающего точность функционирования элементов физических движков. Представлена математическая модель реализации метода на примере двух шаров.

Введение

Физические движки условно делятся на два типа: игровые и научные. В первом случае движок должен работать в режиме реального времени, то есть воспроизводить физические процессы в игре с той же скоростью, с которой они проходят в реальном мире. Вместе с тем от игрового физического движка не требуется точности вычислений. Главное требование — визуальная реалистичность, - и для ее достижения не обязательно проводить точную симуляцию. Поэтому в играх используются «очень сильные» аппроксимации, приближенные модели и другие программные «трюки».

На основе анализа особенностей и возможностей различных физических движков, таких как: ODE, Tokamak, Newton, Karma, PhysX, Bullet и Havok, выделены следующие: кроссплатформенность, большое количество типов тел, большое разнообразие типов соединений, точность просчета физики [1]. Получено, что параметры точность просчета физики, количество типов соединений, количество типов тел, участвующих в столкновениях, могут быть оптимизированы.

Целью работы является разработка математического метода увеличения точности вычислений параметров столкновения тел, реализуемых движком.

Задачи, направленные на достижение цели:

1. Разработка метода расчета параметров столкновения тел, повышающего точность вычислений.

2. Моделирование метода на примере столкновения двух шаров.

Математическое моделирование. Основное отличие предложенного алгоритма физического движка от известных алгоритмов заключается в том, что определение потенциального столкновения в данном временном шаге происходит до того, как тела столкнутся, а не после столкновения, как это обычно бывает. Основной принцип - нахождение ближайшего по времени столкновения в течение данного временного шага, пока столкновения не закончатся или количество столкновений в данном временном шаге не превысит допустимое количество, устанавливаемое пользователем. Благодаря такому методу тела никогда не проникнут друг в друга, благодаря чему повышается точность и адекватность симуляции физики.

Ближайшее по времени столкновение определяется перебором всех тел со всеми, и выбором ближайшего по времени из всех. Если n - это количество тел, то получится n(n)/2 переборов всех тел.

На входе модели присутствуют тела t{t1,t2,…,tn}, их описание (масса m, геометрия g, коэффициенты трения kt и упругости ku), позиции тел P, силы, приложенные к этим телам F{F1,F2,…,Fn}, скорости V и ускорения A тел, и силы G{G1,G2,…,Gn}, приложенные к общему пространству и время T, прошедшее с последнего цикла моделирования. На выходе должны быть адекватно измененные входные параметры F, V, A, P исходя из законов физики в зависимости от времени T.

Так как присутствуют силы и ускорения, значит, изменение скорости тел во времени будет квадратичным:

V = V0 + AT, (1)

где V0 - первоначальное значение скорости. А изменение координат тел во времени:

P = P0 + V0 * T + AT ^ 2 / 2 (2)

где P0 - начальные координаты тела.

Причем V, A, P - могут быть векторами. Так как пространство является трехмерным, значит V, A, P, F,G - будут трехмерными векторами.

Основным элементом программного моделирования в физическом движке является: нахождение параметров столкновения тел.

Возьмем в качестве примера столкновения тел - столкновение двух шаров (Рис.1). На входе имеются массы M1 и M2, радиусы шаров R1 и R2 и векторы скоростей шаров V01 и V02, координаты их центров S01 и S02, векторы сил, приложенные к центрам шаров F1 и F2, и коэффициенты упругости шаров ku1 и ku2.

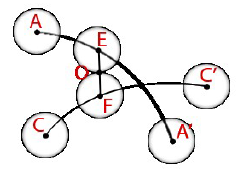
Рисунок 1 - Пересечение траекторий шаров.

Ускорения a1 и a2 можно вычислить по второму закону Ньютона.

Система уравнений пересечения кривых траекторий центров шаров примет вид:

S = S01 + V01 * t + a1 * t2 / 2

S = S02 + V02 * t + a1 * t2 / 2 (3)

- где S - искомая точка пересечения, S01 и S02 - начальные положения центров шаров, V01 и V02 - начальные скорости шаров, a1 и a2 - ускорения шаров, t - время пересечения центров шаров.

Решение этой системы будет иметь вид:

t = ( sqrt ( V01 - V02 ) + 2 * ( a1 - a2 ) * ( S01 - S02 ) - ( V01 - V02 ) ) / ( a1 - a2 ),

S = S01 + V01 * t + ( a1 * t1 ^ 2 ) / 2 (4)

Решением системы уравнений будут: точка пересечения траекторий центров шаров и время столкновения. Ситуация, когда траектории центров шаров пересекаются, практически невозможна, поэтому в систему нужно включить уравнение, учитывающее радиусы шаров (Рис.2).

После этого система уравнений для двухмерного пространства будет иметь вид:

S1 = S01 + V01 * t + a1 * t2 / 2

S2 = S02 + V02 * t + a2 * t2 / 2

S2 - S1 = R1 + R2 (5)

Для трехмерного пространства получается уравнение четвертой степени, и расчет столкновений всех сфер будет занимать много процессорного времени.

Поэтому примем допущение:

- в промежутке времени T одного цикла траектории движения тел будут прямолинейными и равноускоренными. При малом T допущение никак не будет сказываться на точности вычислений.

Рисунок 2 - Пересечение траекторий шаров с учётом их радиусов.

Первой задающей точкой каждой прямой будет начальное положение центра шара. Второй точкой будет являться положение центра шара в момент времени T, вычисленное по формуле (2). Известно, что AE / CF = EB / FD = AB / CD, EO = R1 (радиус первой сферы), OF = R2 (радиус второй сферы).

После подстановок и сокращений полученной системы уравнений имеем уравнение и его решение:

n * t2 + 2 * m * t + p = 0, где

n = (ABx – CDx)^2 + (ABy – CDy)^2 + (ABz – Cdz)^2,

m = (Ax – Cx) * (ABx – CDx) + (Ay - Cy) * (ABy - CDy) + (Az – Cz) * (ABz – CDz) +,

p = (Ax - Cx)2 + (Ay - Cy)2 + (Az - Cz)2 – (R1+ R2)2, (6)

Варианты решения уравнения:

1. Если дискриминант D = m*m - np < 0, то столкновения нет

Если n = 0 , то шары двигаются параллельно

Если t < 0 , то столкновение было в прошлом цикле

Если t > 1, то столкновение будет в следующем цикле

Если 0 < t1 <=1 и 0 < t2 <=1, то следует выбрать наименьший t.

Возможен случай, когда один из шаров не двигается. Центр такого шара будет в точке F. Тогда вышеизложенное решение будет верным, CD = 0, C = F.

Вывод

Сложность разработки движка заключается в необходимости оптимизации алгоритмов, его реализующих, таким образом, чтобы максимально повысить его быстродействие, чтобы при этом не ухудшить точность симуляции. В работе показано, что точность просчета физики может быть увеличена за счет точных алгоритмов определения столкновений, за счет определения потенциального столкновения тел до момента столкновения и адекватного ответа на это столкновение, что полностью исключает проваливание тел друг в друга.

Физические движки, программы, моделирующие физические законы с той или иной степенью точности, очень актуальны в настоящее время. Их востребованность обусловлена необходимостью обучения пилотов самолетов и вертолетов, как гражданских, так и военных, использованием для обучения правилам дорожного движения водителей машин и тяжелой техники, имитации боевых действий и научных экспериментов (научные физические движки), имитации потока воздуха в аэрокамере, и просто обучения физики для школьников или студентов. Физический движок является мощным инструментом моделирования физики в руках обычного пользователя.

Библиографический список

1. “Повышение точности игрового физического движка”, “Информационные технологии в профессиональной деятельности и научной работе”, Василевский И.Ю.
2. Tokamak physics engine - http://dic.academic.ru/dic.nsf/ruwiki/388798
3. Open Dynamics Engine - http://dic.academic.ru/dic.nsf/ruwiki/158171
4. Newton Game Dynamics - http://dic.academic.ru/dic.nsf/ruwiki/536259
5. Karma (физический движок) - http://dic.academic.ru/dic.nsf/ruwiki/606245
6. PhysX SDK (движок) - http://dic.academic.ru/dic.nsf/ruwiki/608439
7. Bullet Physics Library - http://dic.academic.ru/dic.nsf/ruwiki/602887
8. Havok - http://dic.academic.ru/dic.nsf/ruwiki/476945