Авторы: Luigi Cardamone, Georgios N. Yannakakis, Julian Togelius, Pier Luca Lanzi
Перевод: Илькун В.П.
Источник: Politecnico Di Milano, Piazza L. da Vinci, 32 - 20133 Milano, Italy IT University of Copenhagen, Rued Langgaards Vej 7, 2300 Copenhagen, Denmark. Evolving Interesting Maps for a First Person Shooter
Мы обращаемся к проблеме автоматического конструирования карты для игры шутер от первого лица (FPS).Эффективное решение этой проблемы процедурной генерации контента (PCG) позволит создавать FPS игры с более низкой стоимостью разработки с почти бесконечным воспроизведением и возможностью адаптироваться к навыкам и предпочтениям отдельных игроков. Мы предлагаем решение, где карты оптимизируются благодаря функции-соответствия, основанной на среднем времени боя игроков. Для достижения этой цели, четыре различных представления карт тестируются и сравниваются. Полученные результаты демонстрируют явное преимущество некоторых представлений в создании интересных FPS карт и демонстририруют новый подход для автоматической генерации уровней в играх этого жанра.
Процедурная генерация контента, поиск-ориентированность, эволюционные алгоритмы, шутеры от первого лица, опыт игрока, игры
Шутеры от первого лица (FPS) – это видеоигры, где игрок видит игровой мир с точки зрения персонажа, которого он контролирует, и где геймплей включает в себя навигацию в сложной трехмерной окружающей среде и вступление в бой с использованием различных типов оружия. FPS игры в настоящее время являются одним из самых популярных жанров в мире видеоигр, без признаков об уменьшении популярности. Call of Duty, Halo, Battlefield и другие игры серий продают миллионы копий каждый год. Тем не менее, разработчики страдают от роста расходов на разработку контента для таких игр, что приводит к коротким играм и тревогам о креативности и тематическому расхождению от мейнстрима. Типичная современная FPS имеет менее десяти часов однопользовательской кампании и несколько мультиплеерных карт, несмотря на стоимость в десятки миллионов долларов на разработку.
Процедурная генерация контента относится к автоматическому созданию игрового контента, где "контент" широко интерпретируется: уровни, персонажи, звук, предметы, растительность и местность, все рассматривается как контент в процессе разработки. В то время как процедурная генерация содержания в различных формах была вокруг в течение более чем двух десятилетий, она в основном применяется для периферийных элементов игры, и как правило, только в виде случайной генерации в конкретных границах. В противоположность этому, генерация "ядра" контента, такого как карты и уровней, и генерация контента оптимизирующего отдельные аспекты геймплея или оптимизирующего возможности для отдельных игроков, является важной темой исследования, результаты которой до сих пор считаются слишком незрелыми для коммерческих игр. В последнее время, поиск-ориентированный подход к PCG [11], называемый опыт-управляемая PCG получил распространение [13]. При таком подходе эволюционные и другие алгоритмы стохастического поиска используются для поиска контента с помощью некоторой функцией соответствия и предназначены для захвата соответствующих аспектов опыта игрока. Оба представления игрового контента, и разработка функции пригодности представляют интересные задачи исследования. Некоторые попытки для решения этих задач можно увидеть в недавней работе на развивающихся треках для гоночных игр [9], правил для настольных игр [1], оружиях для космических стрелялок [4], уровни для платформы игры [8] и картами для стратегий в режиме реального времени [10]. Вычислительные методы разведки были применены к FPS играм, но в основном для создания поведения NPC различных видов. Некоторые примеры экспериментоируют в оптимизации параметров стандартных сценариев ботов [2], имитирующий стиль игры человеческих игроков [3]. FPS карты были предметом анализа игровой разработки, существует несколько идей по дизайну метрик, которые могут быть полезны для PCG [7], но должны наши лучшие знания не были синтезированы раньше.
Исследования, описанные в этой статье, являются новыми, в основном ориентированными на методики поиска, и используются для создания контента для FPS игр впервые. Статья структурирована следующим образом: в следующем разделе мы представляем Cube 2 игровой движок который будет использоваться для экспериментов, затем мы представим наш общий подход к эволюционной FPS карте, в том числе функции пригодности, далее следуют описания различных представлений карт и экспериментов, мы сравниваем их пригодность для эволюционных играемых карт. В заключительном разделе обсуждаются шаги, которые следует предпринять для того, чтобы усовершенствовать эту технику.
Cube 2 [12] является свободная FPS с открытым исходным кодом, которая поддерживает как одно- так и многопользовательские игры. Cube 2 поставляется с несколькими графическими моделями персонажей, наборами оружия и большим количеством карт. Движок, лежащий в основе Cube 2 быстрый и сложный, что позволяет делать хороший рендеринг с высокополигональным окружением, приближаясь к визуализации в коммерческих играх (см. рисунок 1). Технически, игровой движок основан на 6 направленниях полях высот в структуре мирового октодерева, которая также поддерживает карты освещения с точными тени, динамические шейдеры, частицы и объемные взрывы. Cube 2 также поддерживает простую, но полную конфигурацию / язык сценариев, который позволяет настраивать все меню и большинство других аспектов игры, а также легко добавлять «моды» в игру.
Рисунок 1 - Скриншоты из Cube 2
Одна из выдающихся возможностей движка заключается в возможности доступа к редактированию игровой геометрии, а также многопользовательскому кооперативному редактированию. Интегрированная карта Редактор очень мощный: он позволяет пользователю создавать и редактировать новые объекты, добавлять текстуры, добавлять объекты из различных материалов (таких как вода, лавы и стекло), а также источники света, и ряд других действий. С тех пор как Cube 2 стал с открытым исходным кодом, редактор карт сам по себе может быть изменен и расширен любым способом, который необходи. Эта функция имеет решающее значение для наших целей, так как нам нужно создать эволюционирующие карты в игру, и это является одной из главных причин почему мы решили использовать Cube 2, а не другие известные коммерческие FPS игры. Другой основной причиной является то, что движок игры позволяет запускать игры в «безголовом» режиме, т.е. без визуализации, где они могут быть ускорены настолько быстро, насколько разрешает процессор.
В этой работе мы применяем эволюционные алгоритмы для эволюционных карт для многопользовательской FPS игры. Многопользовательская FPS – это игра, где несколько игроков (людей и / или ботов) вступают в бой на той же карте. Несколько режимов игры возможны с некоторыми различиями в правилах, а в основном режиме, "Матч смерти", правила просты: когда персонаж будет убит, он появится в другой точке карты после нескольких секунд. Игра заканчивается по истечении определенного количества времени, и игрок с наибольшим количеством фрагов (то есть количеством противников, которых он убил) выигрывает игру.
FPS карты обычно состоят из серии комнат и коридоров, а также некоторых точек респауна и ресурсов (либо оружия или бонусов). Карты могут иметь несколько различных уровней с этажами над и под друг другом, и такие функции как лестницы, пандусы и лифты для перемещения вертикально между этажами. В этой работе мы сосредоточимся на картах только с одним полом.
Целью данной работы является создание карт с потенциалом для интересного геймплея. Принято считать, что некоторые FPS карты являются более интересным и глубокими по геймплею, чем другие, например, вознаграждая умелое использование комплекса тактик, и заставляя игроков изменять свою тактику, так что они не могут использовать один и тот же приём все время, чтобы победить. Принято считать, что такие карты лучшего качества, чем другие. Действительно, большая работа проделана в балансировке из тех карт, которые доступны в виде платных загрузок для популярных игр FPS, и вы убедитесь, что нет такой стратегии, которая будет доминировать на карте. Для краткости мы будем называть карты с потенициально интересным геймплеем перспективными картами.
Естественно, что трудно разработать точные оценки перспективных карт, так как это потребует прогнозирования предпочтений большого количества игроков (например, как и в [8]). В будущем мы планируем разработать более сложные функции пригодности, основанные на управляющих данных о возможностях и предпочтениях игрока. На данный момент, мы будем остановимся на простой теории функции пригодности.
Будем считать, что перспективная карта напрямую связана с временем боя игрока, который определяется как продолжительность от момента, в котором игрок начинает бороться с противником, до момента, когда игрок будет убит. Так как во время всего матча игрок умрет и воскреснет несколько раз, мы можем вычислить среднее значение времени боя каждого игрока, Tf. А малое значение Tf означает, что игрок погибает очень быстро после начала боя с противником. Если значение Tf является большим, это означает, что после того, как игрок впервые получает повреждения в бою, он выживает и может продолжить бой, потому что карта дает возможности убежать, спрятаться, получить бонусы здоровья и лучшее оружие. С тех пор как FPS карты предоставляют функции, которые, со стратегической точки зрения, могут быть использованы для участия игрока в более длинных и интересных боях, Tf является хорошим показателем перспективных карт.
Лучший способ оценить значение Tf карты будет игра в несколько матчей с пользователями на этой карте и сбор статистики, уступая интерактивным функциям пригодности в соответствии с классификацией в [11]. К сожалению, ипользование пользователей в наших экспериментах не практично, потому что это потребует от них играть тысячи матчей (в будущем, это может быть использовано в массивных многопользовательских играх, это похоже на подход, принятый в [4]). Вместо этого мы моделировали матчи по 10 минут между 4 ботов и измеряли среднее Tf у всех ботов (вектор TF).
Полная функция пригодности имеет другой компонент в дополнение к Tf: свободное место на карте, S. Мы хотим, чтобы наша пригодность содействовала генерации больших карт, так как маленькие карты не оставляют достаточно места для размещения оружия и точек респауна, что приводит к нереальным значениям Тf. Стоит отметить, что максимальный размер карты ограничен и что в лучшем случае карты генерируется (см. раздел 5) с атрибутом S, который менее чем 20% от общей функции пригодности. Учитывая вышеизложенное, полную функцию пригодности карты запишем следующим образом:
f = TF + S (1)
Где TF измеряется в миллисекундах, и это целое число, большее 0, S означает количество свободных клеток на карте и ограничено между 0 и 4096.
Для оценки карт с использованием моделируемых матчей мы должны были решить два основных вопроса: генерация точек пути и ускорение игры. В то время как для последнего решение было столь же просто, как и отключение графического рендеринга (позволяет моделирование матча в 10 минут уменьшить до 10 секунд с помощью компьютера 3,00 ГГц Intel Core 2 Duo Processor), в первом случае мы должны были реализовать алгоритм размещения точек. Боты, доступные в Cube 2, как и во многих коммерческих играх, зависит от списка точек пути для навигации в данной карте. Исходя из этого, точки представлены в виде графика, на котором боты применяют обычный А* алгоритм для перемещения между бонусами, оружием и врагами. Поэтому была необходима для генерация точек пути на лету для каждой новой карты. К сожалению, игра не дает никакой поддержки для автоматической генерации точек пути, поскольку они обычно создаются дизайнером карты вручную. Для решения этой проблемы мы реализовали алгоритм генерации точек путей, которая состоит из следующих этапов: (I) вычисления свободных клеток карты; (II) размещения точек путей на каждую свободную клетку; (III) подключение каждой точки пути с четырьмя соседями (вверху, внизу, слева, справа), и если нет никаких препятствий между ними; (IV) присоединить каждый ресурс на карте к сетке из точек пути.
После функции пригодности, другой важный выбор при создании в поисковых системах PCG состоит в том, как представить контент. Представление должно позволять широко представить весь спектр контента, но также позволять производить быстрый поиск для нахождения в контенте с высоким значением пригодности. В этой статье мы предлагаем для сравнения четыре различных представления FPS карт.
Во-первых, мы должны различать генотип и фенотип этих карт. Фенотип – это изоморфные карты в игре. Для всех представлений карт, структура фенотипа такая же: матрица 64 х 64 клетки. Каждая клетка представляет собой небольшой кусок карты, содержащий, например, персонажа игрока. Каждая ячейка может быть либо свободным пространством или стеной (с фиксированной высотой). Каждое свободное пространство может быть пустым или содержать точку респауна или предмет (оружие или бонус здоровья). Фенотип сохранен в текстовом файле и загружается в игру с помощью специального загрузчика, который мы реализовали в Cube 2.
Структура генотипа, с другой стороны, является различным для каждого пред- ления. Генотип – это то, что выделяется при генетическом алгоритме. Каждое представление поставляется с процедурой построения фенотипа с генотипом. Когда генотип оценивается, происходит следующее:
1. Генотип используется для построения фенотипа;
2. Затем фенотип дает определенную карту для Cube 2 и моделируемый матч начинается на этой карте;
3. Статистические данные, собранные во время матча, используемые для расчета пригодности.
Четыре представления описаны ниже в порядке убывания непосредственности.
Самое непосредственное представление называется «сетки» и предполагает, что начальная конфигурация карты представляет собой сетку из стен. В частности 9 на 9 сетка используется для разделения карты на 81 квадрат. Каждый квадрат из сегмента стены может быть удален, чтобы создавать комнаты и коридоры. Геном представляет собой какой из этих сегментов стены активен (ON), а какой нет (OFF). В соответствии с представлением в виде сетки схема каждого гена кодирует состояние двух сегментов ячейки стены: один на вверху и один справа. Таким образом, каждый ген может принимать четыре значения: 0, если оба сегменты стены не горят, 1, если только верхний сегмент находится на стене, 2, если только правый сегмент находится на стене, и 3, если оба ON.
Второй, менее непосредственное представление называется Всё-Белое. Оно предполагает, что
начальная карта пуста (со стенами только на границах) и добавляет элементы стены на пустое пространство.
Геном кодирует количество блоков стен, Nw (Nw составляет 30 в данной работе), каждый из которых представлен тремя значениями,
Третье представление называется Всё-Черное и является, в некотором смысле, точной
противоположностью представлению Всё-Белое. Это представление начинается с
карты полной блоков стен, и постепенно добавляет свободное пространство.
Геном кодирует количество пустых мест двух типов: арен и
коридоров. Арен квадратными ячейками определяется триплет
Наиболее необычное представление называется Случайное-Копание и как Всё-Чёрное представление,
оно строит карты из начальной конфигурации, которая полностью состоит из блоков стен.
Геном кодирует поведение очень простого агента, который
движется вокруг и освобождает пространство в каждой клетке, которую он посетил, таким образом, напоминающее
черепаший график. Полученная карта является следом пути агента следующим
фиксированное число шагов. Агент стартует в центре карты и ее
поведение представлено четырьмя вероятностными значениями:
Первые три представления могут генерировать карты с частями, которые являются недоступными из других частей карты. Существуют два основных подхода для преодоления этой проблемы. Первый подход пытается восстановить карту так, чтобы он становилась полностью доступной. Это решение имеет несколько недостатков: это сложно в реализации, это требует вычислительных ресурсов и может сильно изменить исходную форму карті. Второй подход ориентирован на простое удаление недоступных частей из окончательного карты. В данной работе мы будем использовать второй подход путем выявления всех ячеек, из которых можно добраться до центральной точки карты, а затем удалять все клетки, которые не доступны.
Перед окончанием создания Cube 2 карты из фенотипа, мы должны добавить точки респауна, оружие и бонусы здоровья. Мы делаем это с помощью простой равномерно-распределенной эвристики следующим образом: (I) матрицы фенотипа делится на квадратные блоки; (II), для каждого блока вычисляет количество свободных клеток; (II) если это число больше, чем заданное пороговое для двух точек респауна или одного предмета (оружия или бонуса здоровья), то размещаем это внутри блока.
Для развития карт, мы применили простой генетический алгоритм со стандартными операторами: отборочный турнир с размером 2, одна точка пересечения, частоту мутаций 1 / n (где n – длина генома), мутация в диапазоне от 0.2 (в соответствии с равномерным распределением) и кроссовер с вероятностью 0.2. Параметры генетического алгоритма были установлены эмпирически. Мы применили генетические алгоритмы с численностью населения 50 человек, и дали ему работать в течение 50 поколений. Каждый эволюционный запуск занимал примерно 6 часов до завершения и эксперимент повторяли 10 раз для каждого представления.
На рисунках 2, 3, 4 и 5 выведены на экран четыре самые высокопроизводительные эволюционные карты каждого представления. 2D изображение каждой карты иллюстрирует как черные стены сегментов, синими точками – точки респауна, и предметы (оружие и бонусы здоровья) в качестве зеленых точек. Рисунок 6 иллюстрирует, как развивалась одна из лучших карт в 3D, когда они загружаются в Сube-2. Для проверки значения, мы запускали t-тест по 10 раз для всех представлений. По результатам: (I) Всё-белое генерирует карты, которые являются статистически лучше, чем Всё-чёрные и Случайно-Вскопанные (величина р < 0,001 в обоих сравнениях); (II) Всё-белые развивалась лучше, чем карты-сетки, но разница не является статистически значимой (р-значение = 0.141), (??III) карты-сетки являются статистически лучше, чем Всё-черное и Случайно-Вскопанные карты (величина р < 0,001 в обоих сравнениях) и (IV) карты, составленные Всё-Чёрное статистически лучше, чем Случайно-Вскопанные (величина р <0,001). Кроме того, были проведены эксперименты для проверки чувствительности значения пригодности, оценивая карту несколько раз. Даже несмотря на то, что дисперсия пригодности может быть достаточно большой и зависит от структуры карты, первичное размещение ботов, оружие и поведение ботов упорядочено среди четырех представлений и сохраняет статистический эффект.
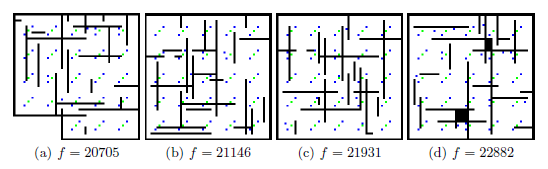
Рисунок 2 - Лучшие эволюционные карты использующие представление Всё-белое
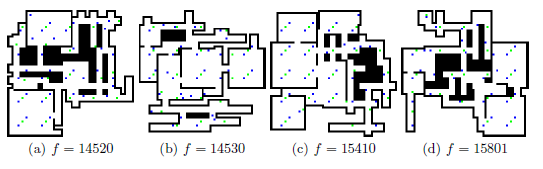
Рисунок 3 - Лучшие эволюционные карты использующие представление Всё-черное
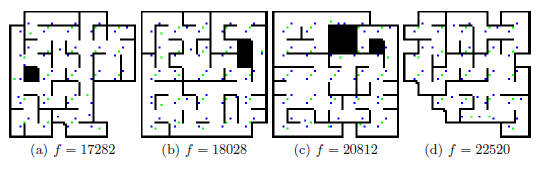
Рисунок 4 - Лучшие эволюционные карты использующие представление Сетка
Рисунок 5 - Лучшие эволюционные карты использующие представление Случайное-вскапывание
Рисунок 6 - Одна из лучших эволюционных карт (f = 21931) загруженных в Cube 2
Как видно из полученных результатов, все четыре представления могут быть использованы для получения эволюционных карт. Каждое представление создаёт некоторые своеобразные черты, характеризующие сильно эволюционировавшие карты. Случайное-вскопанное представление порождает много карт с длинными коридорами и несколькими небольшими аренами. Всё-чёрное представление генерирует несколько больших арен, в то время как коридоры, как правило, короче и могут заканчиваться тупиками. Сетка-представление создает очень интересные карты с высокой степенью симметрии. Наконец, Всё-белое представление порождает лучшие карты в соответствии с функцией пригодности. Высокие значения пригодности Всё-белых карт оправданы соединением многих узких проходов с большими аренами, которые генерируются большинством небольших пространств для игрока, помогающими скрываться и ловить своего оппонента или найти бонусы здоровья после драки.
Мы разработали четыре различных представления для карт шутеров от первого лица, и функцию пригодности для вычисления их потенциала интересного геймплея. Мы также выполнили ряд экспериментов, чтобы убедиться, что мы можем эволюционировать FPS карты, используя эти представления и функцию пригодности. Кроме того, мы использовали функцию пригодности для сравнения перспектив эволюционных карт с каждым из представлений. Из полученных результатов можно сделать вывод, что Всё-белое и сетка-представление имеют явные преимущества.
Несколько законных возражений могут быть выдвинуты против нашей функции пригодности, и каждое из них предлагают возможности для будущей работы. Одно из возражений, что это зависит от логики управления ботами в Cube 2. Это логика управления не была, представлена в работе, и в самом деле не совсем прозрачна. Использование специально разработанных ботов позволит нам настроить функцию пригодности более подробно, а также изучить новые функции, такие как производительность численно или тактически превосходящей команды против слабой. Настройка поведения ботов, чтобы соответствовать человеческому стилю игры может также улучшить функцию пригодности; ключи к тому как это сделать могут быть взяты из соревнования 2k BotPrize [5]. Другое возражение заключается в что мы еще не подтвердили эффективность нашей функции пригодности, и поэтому не можем утверждать, что наша мера интересного геймплея соответствует ожиданиям игроков. Исследования пользователя в настоящее время наш главный приоритет, и наши предварительные результаты показывают, что игроки предпочитают карты с более высокой пригодностью. Следуя принципам представленным в [13, 8] мы также планируем изучить влияние на создание карт нескольких эмоциональных состояний игроков, и синтезировать модель игрового опыта поведения игрока и создание FPS карты. Эти модели могут быть использованы для построения адаптивной игры FPS, которая создаёт карты в соответствии с навыками и предпочтениями для отдельных игроков (или группы игроков), чтобы создать оптимальную привлекательный геймплей.
1. Browne, C.: Automatic generation and evaluation of recombination games. Ph.D.
thesis, Queensland University of Technology (2008)
2. Cole, N., Louis, S.J., Miles, C.: Using a genetic algorithm to tune first-person
shooter bots. In: Proceedings of the IEEE Congress on Evolutionary Computation.
pp. 139–145 (2004)
3. Gorman, B., Thurau, C., Bauckhage, C., Humphrys, M.: Believability testing and
bayesian imitation in interactive computer games. In: Proceedings of the Conference
on Simulation of Adaptive Behavior (SAB) (2006)
4. Hastings, E.J., Guha, R.K., Stanley, K.O.: Evolving content in the galactic arms
race video game. In: Computational Intelligence and Games, 2009. CIG 2009. IEEE
Symposium on. pp. 241–248 (Sept 2009)
5. Hingston, P.: A new design for a turing test for bots. In: Proceedings of the IEEE
Conference on Computational Intelligence and Games (CIG) (2010)
6. van Hoorn, N., Togelius, J., Schmidhuber, J.: Hierarchical controller learning in a
first-person shooter. In: Proceedings of the Symposium on Computational Intelligence
and Games (CIG) (2009)
7. Hullett, K., Whitehead, J.: Design patterns in fps levels. In: FDG ’10: Proceedings
of the Fifth International Conference on the Foundations of Digital Games. pp.
78–85. ACM, New York, NY, USA (2010)
8. Pedersen, C., Togelius, J., Yannakakis, G.N.: Modeling Player Experience for Content
Creation. IEEE Transactions on Computational Intelligence and AI in Games
2(1), 54–67 (2010)
9. Togelius, J., De Nardi, R., Lucas, S.M.: Towards automatic personalised content
creation in racing games. In: Proceedings of the IEEE Symposium on Computational
Intelligence and Games (CIG) (2007)
10. Togelius, J., Preuss, M., Beume, N., Wessing, S., Hagelb?ack, J., Yannakakis, G.N.:
Multiobjective exploration of the starcraft map space. In: Proceedings of the IEEE
Conference on Computational Intelligence and Games (CIG). pp. 265–272 (2010)
11. Togelius, J., Yannakakis, G.N., Stanley, K.O., Browne, C.: Search-based procedural
content generation. In: Proceedings of EvoApplications. vol. 6024. Springer LNCS
(2010)
12. V/A: Cube 2: Sauerbraten. http://sauerbraten.org/
13. Yannakakis, G.N., Togelius, J.: Experience-driven Procedural Content Generation.
IEEE Transactions on Affective Computing (2011)