В конце 2006 г. очередного масштабного успеха в части атак на алгоритм MD5 и его приложения добились Стивенс, Ленстра и де Вегер. В ряде своих работ, вышедших в 2006-2007 гг. (в частности, в работах [1-3]), они предложили методику поиска коллизий для сообщений, префиксы которых имеют различающиеся хэш-значения (коллизия с выбранным префиксом – chosen-prefix collision). В качестве практического примера применения данной методики ее авторы разработали способ конструирования пар сертификатов X.509, принадлежащих различным пользователям и имеющих различающиеся значения открытых ключей, но при этом дающих коллизию.

Во второй и третьей частях статьи мы рассматривали различные варианты «расширения» коллизии MD5, включая предложенный в 2005 г. Ленстрой, Ванг и де Вегером метод конструирования пары сертификатов с различными значениями модулей открытых ключей, но с эквивалентными хэш-значениями. Все эти методы основывались на абстрактной коллизии, например, «двухстороннее расширение»:

MD5(t || x’ || q) = MD5(t || y’ || q),

в основе которого лежала двухблочная коллизия x’ и y’.

Двухблочная коллизия возникала при использовании нестандартного вектора инициализации – MD5(t). Тем не менее, префикс сообщения t был эквивалентен для обоих сообщений, что существенно сужало возможности по практическому использованию коллизий.

Принципиальное отличие коллизий с выбранным префиксом состоит в том, что начальные блоки дающих коллизию сообщений (префиксы) могут быть полностью различными: методика поиска коллизий с выбранным префиксом позволяет для любых сообщений x и y найти такие последовательности q₁ и q₂, что [1] (см. рис. 1):

MD5(x || q₁) = MD5(y || q₂.).

Такая коллизия существенно более универсальна и обладает несравнимо большими возможностями по применению на практике.

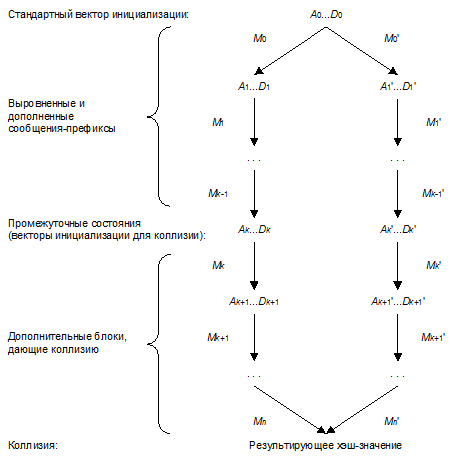
В [2] методика конструирования коллизии с выбранным префиксом описана подробно; ее основные этапы состоят в следующем (см. рис. 2):

1. Выбираются сообщения, для которых будет формироваться коллизия, т. е. сообщения-префиксы x и y. Размер сообщений-префиксов должен быть сравним с 416 по модулю 512; при необходимости, сообщения дополняются любыми данными до требуемого размера.
2. Сообщения-префиксы дополняются 96-битовыми строками, которые в результате их обработки функцией сжатия алгоритма MD5 формируют между промежуточными состояниями A_k…D_k и A_ksub>’…D_k’ разность специального формата.
3. Результирующие сообщения дополняются несколькими (в основном варианте атаки – восемью) 512-битовыми блоками данных, каждая пара которых дает near-коллизию с меньшим количеством различающихся битов, чем предыдущая; в результате обработки последнего из этих блоков формируется коллизия.

Таким образом, значения q₁ и q₂ состоят из 96-битовых дополнений и восьми пар блоков, т. е. полный размер каждого из дополнений составляет 4192 битов. Трудоемкость поиска последовательностей q₁ и q₂ определяется, в основном, трудоемкостью поиска 96-битовых дополнений и составляет 2⁵⁰-2⁵² операций. Авторы атаки предложили также ее вариант с эквивалентной трудоемкостью, в котором не требуется наличие 96-битовых дополнений, но количество пар дополнительных блоков увеличено до 14, что сужает возможности практического применения атаки [2].

Стивенс, Ленстра и де Вегер применили данную методику для создания пары сертификатов X.509 (которая будет рассмотрена далее), для чего ими были применены распределенные вычисления с использованием до 1200 компьютеров в течение 6 месяцев. При этом, в [2] сказано, что этот поиск шел не по оптимальному пути и, с использованием накопленного опыта, аналогичную атаку можно выполнить примерно за 2 месяца при наличии эквивалентных ресурсов.

Рис. 1 Коллизия с выбранным префиксом

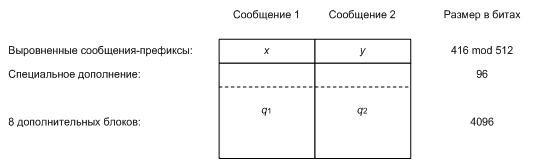
Рис. 2 Структура пары сообщений

Рассмотрим способ конструирования пары сертификатов с эквивалентными и верными электронными подписями, но с различными уникальными именами пользователей, основанный на коллизии с выбранным префиксом и подробно описанный в [2] и [3]. Последовательность создания пары сертификатов состоит из следующих шагов (см. рис. 3):

1. Формируется шаблон сертификата. Как и в более ранних работах Ленстры, Ванг и де Вегера (при создании пары сертификатов с эквивалентными именами пользователей – подробно см. в [4]), предполагается, что сертификаты должны предназначаться для использования в алгоритмах RSA, соответствовать формату X.509 и кодироваться методом ASN1.DER. Кроме того, для успешного формирования коллизии с выбранным префиксом поля каждого из сертификатов, находящиеся до поля «Модуль открытого ключа», должны иметь совокупный размер на 96 битов меньше кратного 64 байтам (512 битам).
2. Данные поля сертификатов заполняются необходимой атакующим информацией, которая эквивалентна во всех полях, кроме следующих:
   • полей серийных номеров сертификатов, которые являются уникальными для различных сертификатов;
   • полей уникальных имен пользователей.

Отметим, что последнее поле является композитным и, помимо собственно имени пользователя, может содержать дополнительную информацию, в частности, об организации, в которой работает пользователь. Авторы атаки при создании первой пары сертификатов по своей методике присвоили им имена «Arjen K. Lenstra» и «Marc Stevens», после чего для обеспечения выравнивания согласно изложенному выше требованию использовали поле организации, записав в него, соответственно, значения «Collisionairs» и «Collision Factory».

Заполненные поля двух сертификатов (до поля «Модуль открытого ключа») представляют собой сообщения-префиксы x и y.

3. Сообщения-префиксы (без предусмотренного алгоритмом MD5 дополнения) прогоняются через алгоритм хэширования MD5; в результате получаются два значения вектора инициализации, для которых будет осуществляться поиск коллизии.
4. Коллизия формируется с помощью значений модуля открытого ключа n₁ (для первого сертификата) и n₂ (для второго сертификата), которые имеют следующую структуру:

n₁ = Sa || Sb || B;

n₂ = Sa’ || Sb’ || B,

где:

• Sa и Sa’ – это 96-битовые дополнения, приводящие к разности специального формата между промежуточными состояниями;
• Sb и Sb’ – это 8-блочные дополнения, приводящие к коллизии в результате обработки алгоритмом MD5;
• B – 4000-битовая последовательность, эквивалентная для обоих модулей (см. далее).

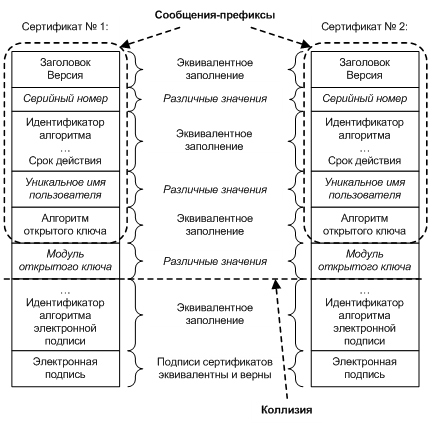
Рис. 3 Пара сертификатов с различными уникальными именами пользователей

Структура модулей n₁ и n₂ приведена на рис. 4.

Коллизия достигается с помощью вычисления пар значений (Sa, Sa’) и (Sb, Sb’), которые согласно описанной выше схеме поиска коллизии с выбранным префиксом представляют собой 4192-битовые последовательности q₁ и q₂:

q₁ = Sa || Sb;

q₂ = Sa’ || Sb’.

После данных значений сертификаты могут быть дополнены только эквивалентными последовательностями. Однако, необходимо сформировать корректные значения модулей n₁ и n₂, для чего выполняется (аналогично описанному в [4] поиску значений b, но с увеличенной размерностью) поиск такого 4000-битового значенияB, которое давало бы в результате два корректных (разлагаемых на произведение больших простых чисел) модуля размером 8192 битов каждый:

n₁ = (Sa *2⁴⁰⁹⁶ + Sb) * 2⁴⁰⁰⁰ + B;

n₂ = (Sa’ *2⁴⁰⁹⁶ + Sb’) * 2⁴⁰⁰⁰ + B.

Рис. 4 Структура модулей открытого ключа

После этого формирование пары сертификатов завершено. Любой из сертификатов может быть обработан алгоритмом хэширования MD5 и подписан; вычисленная для любого из пары сертификатов электронная подпись будет верна и для второго сертификата. При этом сертификаты будут принадлежать различным пользователям, что существенно усилит результативность атаки и позволит, в частности, подделывать подпись владельца парного сертификата. Авторы атаки, однако, отмечали в [2], что им не удалось найти доказуемый эффективный сценарий атаки с использованием такой пары сертификатов, поскольку для ее реализации злоумышленнику требуется контроль над сертификационным центром.

Отметим, что методика является достаточно гибкой и позволяет создавать другие варианты пар сертификатов, например, поля срока действия сертификатов также могут быть заполнены различной информацией – т. е. созданные сертификаты будут обладать различным сроком действия [2].

Наиболее эффектным применение коллизий с выбранным префиксом выглядит именно в части создания пар сертификатов, что не исключает любые другие из описанных ранее возможностей (например, описанные в [5] варианты использования коллизии в качестве переключателя функционала или содержимого программы или документа). Некоторые дополнительные сценарии атак с использованием коллизий с выбранным префиксом описаны, в частности, в [6].

Литература

1. Stevens M., Lenstra A. K., de Weger B. Colliding X.509 Certificates for Different Identities. // http://www.win.tue.nl – October 23, 2006 – Last Updated January 1, 2009.
2. Stevens M., Lenstra A., de Weger B. Chosen-prefix Collisions for MD5 and Colliding X.509 Certificates for Different Identities. // http://www.iacr.org – 2007.
3. Stevens M., Lenstra A., de Weger B. Target Collisions for MD5 and Colliding X.509 Certificates for Different Identities. // http://eprint.iacr.org – Version 1.1 – 4th November 2006.
4. Панасенко С. Обзор атак на приложения и протоколы, использующие алгоритм MD5, часть 3. // Sec.ru. – http://daily.sec.ru/publication.cfm?pid=40095 – 10.04.2013 г.
5. Gebhardt M., Illies G., Schindler W. A Note of the Practical Value of Single Hash Collisions for Special File Formats. // http://csrc.nist.gov – 31 October 2005 – BSI, Bonn, Germany.
6. Stevens M. M. J. On Collisions for MD5. Master’s Thesis. // http://www.win.tue.nl – Eindhoven University of Technology – June 2007.