Задача выполнимости булевых формул (SAT) — важная для теории вычислительной сложности алгоритмическая задача.
Экземпляром задачи SAT является булева формула, состоящая только из имен переменных, скобок и операций И, ИЛИ и HE. Задача заключается в следующем: можно ли назначить всем переменным, встречающимся в формуле, значения ложь и истина так, чтобы формула стала истинной.
Известно, что задача SAT является NP-полной, а значит, в общем случае ее решение является трудно вычислимым. Однако на практике иногда приходится пользоваться такими «методами грубой силы».
Естественно решать такую сложную задачу на распределенных системах с большой вычислительной мощностью.
Написать программу, решающую задачу выполнимости для функции, заданной в файле в формате DIMACS CNF.
Программа должна использовать интерфейс MPI для эффективной работы на системах с распределенной памятью.
Определения.
Булевой называется переменная, принимающая значения - 0 (false) или 1 (true).
Литералом (literal) называется булева переменная или ее отрицание.
Клозом (clause) называется дизъюнкция конечного множества литералов, не содержащая одновременно переменную и ее отрицание.
Единичный клоз (unit clause) – клоз, содержащий ровно один литерал.
Чистый литерал (pure literal) – литерал, отрицание которого не входит в формулу.
Для решения задачи был выбран классический, высокоэффективный алгоритм DPLL, на котором основана реализация некоторых современных SAT-солверов.
Описание алгоритма.
Наиболее простой вариант алгоритма можно описать следующим псевдокодом:
function DPLL(Φ)
if Φ is identically true
then return true;
if Φ is identically false
then return false;
for every unit clause l in Φ
Φ=true-literal-assign(l, Φ);
for every literal l that occurs pure in Φ
Φ=true-literal-assign(l, Φ);
l := choose-literal(Φ);
return DPLL(Φ AND l) OR DPLL(Φ AND NOT(l));
В этой записи использованы следующие обозначения:
true-literal-assign(l, Φ) – возвращает КНФ, полученную из Φ присвоением литералу l значения true.
choose-literal(Φ) – возвращает некоторый литерал, входящий в Φ.
Реализации алгоритма DPLL отличаются дополнительными методами, используемыми при упрощении КНФ, а так же способом выбора литерала, по которому производится расщепление (функцией choose-literal).
Из описания алгоритма видно, что поиск решения производится в некотором дереве, в вершинах которого находятся частично решенные КНФ.
В представленной реализации главный процесс делает несколько первых итераций алгоритма. После вычисления достаточного количества вершин – листья дерева передаются различным узлам, которые параллельно проводят вычисления до конца.
Ниже представлен код, формирующий список КНФ, которые будут решаться параллельно.
К задаче выполнимости может быть достаточно просто сведено большое количество задач дискретной математики.
Для тестирования была взята задача об N ферзях.
Постановка задачи: на шахматной доске размером NxN требуется разместить N ферзей таким образом, чтобы ни один из них не находился под атакой.
Рассмотрим одно из ее возможных сведений к задаче выполнимости.
1. В каждой строке должна быть хотя бы одна 1
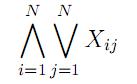
2. В каждой строке должно быть не более одной 1
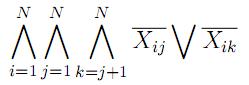
3. В каждом столбце должно быть не более одной 1
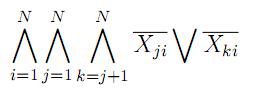
4. На главных диагоналях должно быть не более одной 1
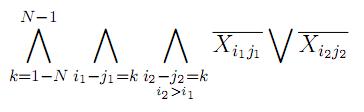
5. На побочных диагоналях должно быть не более одной 1
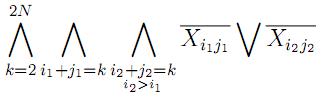
Время работы алгоритма DPLL зависит от правил, применяемых для упрощения КНФ, а также правила выбора расщепляющего литерала. Однако, как и практически все алгоритмы решения задачи выполнимости, в гораздо более существенной мере оно зависит от свойств решаемой задачи.
Получение приемлемо точной теоретической оценки даже для конкретной КНФ является нетривиальной задачей.
Оценим теоретическое время решения КНФ задачи об N ферзях методом полного перебора.
Количество переменных в КНФ : n = N*N
Тогда, для того что бы найти решение нужно осуществить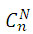 
проверок
Теперь приведем оценку для количества клозов в задаче об N ферзях:
Если p процессов , то число элементарных операций, которое потребуется для каждого процесса составит:
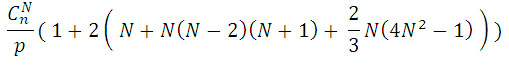
Коммуникационная сложность параллельного алгоритма определяется из соотношения:
Общая оценка трудоемкости параллельного алгоритма:
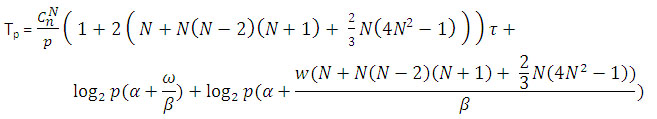
Вычислительные эксперименты для оценки эффективности параллельного алгоритма Прима проводились при следующих условиях и оборудовании:
Tp* - практическое время выполнения алгоритма DPLL
Tp - теоретическое время выполнения алгоритма полного перебора
Работу выполнили студенты группы 84-09 факультета ВМК Носов Сергей Николаевич и Шагин Дмитрий Николаевич.