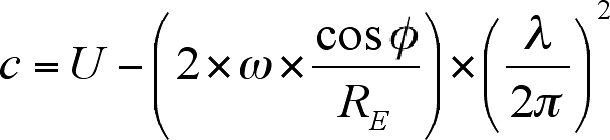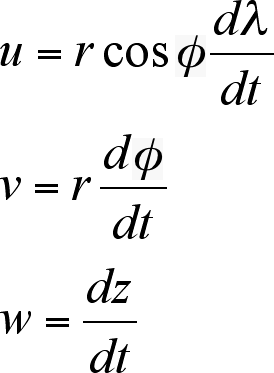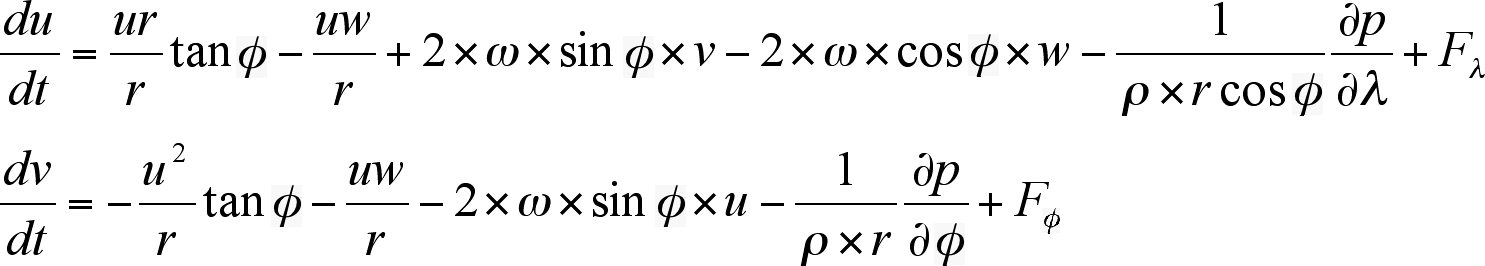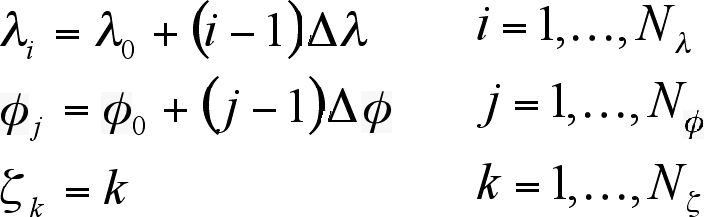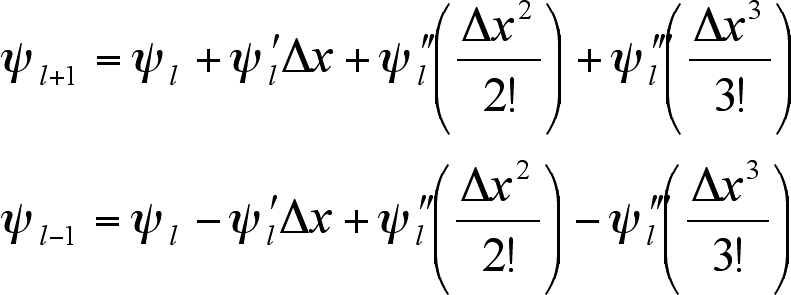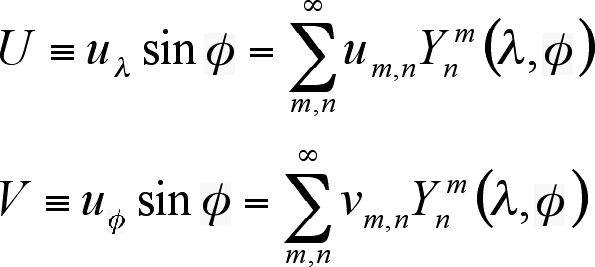History topic:
The History of Weather Forecasting
CONTENTS
1
Introduction
2
Early Forecasting
2.1
First Attempts
2.2
Establishing Weather Services
3
Numerical Weather Prediction
3.1
Finding the Maths
3.2
Computers and Chaos
3.3
Primitive Equations
4
Forecasting Models Used Today
4.1
The Finite Difference Method
4.2
The Spectral Method
4.3
The Finite Element Method
4.4
Current Research
5
Conclusion
1) Introduction
It is one of the most
common topics of conversation, it has influenced people's lives for thousands
of years, and predicting it requires the most powerful computers on the planet:
the weather. Most ancient cultures include weather gods, and weather catastrophes
have an important role in creation myths of many cultures, for example the
Deluge described in the Bible [48]. Observing the skies and drawing the correct
conclusions from these observations was crucial to people's survival [26].
Nowadays, we are more independent of weather conditions due to central heating,
air conditioners, greenhouses and so forth, but weather forecasts are more
accurate than they ever were [21]. Forecasts, both for the next couple of hours
and for the next couple of days, are issued daily. Apart from helping people
decide when they should invite their neighbours for a barbecue, weather
forecasts provide vital information for a wide range of occupational categories
such as farmers, pilots, sailors and soldiers. Furthermore, thanks to
forecasts, people are less likely to be surprised by severe weather; and people
suffering from hay fever for example can time their outdoor activities
according to pollen flight forecasts. The great success of the weather channel
in U.S. television and the fact that weather reports often have a higher
audience rate than the preceding news broadcasts, illustrate that forecasting
has become a highly competitive business [21].
But how are weather forecasts created? And why has forecast accuracy improved
so dramatically over the last couple of decades? In this article, I will
examine the history of weather forecasting, and especially the historical
development of the use of mathematics in forecasting, before describing the
basic principles of the mathematical methods used in current forecasting
models. I will also present some of the current research projects in weather
forecasting.
Chapter 2 of the article
provides an overview of early forecasting attempts, from the first observations
made by ancient cultures to the development of government-supported weather
services.
Chapter 3 reviews the use
of mathematics in weather forecasting, starting with the fathers of numerical
weather prediction, Vilhelm Bjerknes and Lewis Fry Richardson. Then, the
seminal work of Carl-Gustaf Rossby is treated briefly, before the use of
computers in weather forecasting, pioneered by Jule Charney (and others), and
the application of chaos theory to meteorology by Edward Lorenz are discussed.
Moreover, the primitive equations describing atmospheric processes, which are
used in forecasting models, are presented and explained as well.
Chapter 4 presents the two
most important mathematical methods used in forecasting today, namely the
finite difference method and the spectral method, along with the corresponding
grid models applied to the atmosphere. The finite element method, which is
another method for numerically solving partial differential equations, is
described briefly. An overview of some of the current research projects and research
areas in weather forecasting is also given.
This article should be
understood by undergraduate maths or physics students who have taken 2000-level
maths courses offered by the university. The reader does not need to have much
background in applied mathematics or physics, but is expected to know basic
physical principles, for instance gravity, centrifugal force, friction and
waves. Furthermore, I have assumed that the reader is familiar with
differential equations, differentiation of functions of several variables,
Fourier series and Gaussian elimination. Explaining these concepts would have
gone beyond the scope of this article. For similar reasons I have chosen not to
explain less familiar methods, for instance the Galerkin, the least-square and
the Runge-Kutta methods. The reader is kindly asked to look up these methods
(and any other unfamiliar mathematical concepts) in appropriate textbooks.
However, as the article should provide only an overview of the mathematical
methods used in current forecasting models, I have chosen to include only
simple equations and explain some mathematical symbols in order to make
understanding the methods easier. Also, a number of mathematical concepts are
explained in words rather than with equations. While I have assumed that the
reader has a good grounding in general knowledge, I explain several
meteorological terms.
The aim of the article is
to give the reader a summary of the historical development of both weather
forecasting in general as well as the application and the importance of
mathematics in forecasting in particular. In addition, it should give an
impression of how sophisticated mathematical models have to be in order to
accurately simulate and predict the state of the atmosphere and hence the
weather.
2) Early Forecasting
Weather has always played an
important role in people's lives, and attempts to predict weather changes were
made early on. For a very long time, forecasts were based on observations of
the skies both during the day and at night. From the 17th century onwards,
scientists were able to measure factors related to weather such as pressure and
temperature. This helped them understand the atmosphere and its processes
better, and they began to collect weather observation data systematically. By
the end of the nineteenth century, several European countries and the United
States had established the first weather services.
2.1)
First Attempts
It is not known when people
first started to observe the skies, but at around 650 BC, the Babylonians
produced the first short-range weather forecasts, based on their observations
of the stars and clouds. The Chinese also recognised weather patterns, and by
300 BC astronomers had developed a calendar which divided the year into 24
festivals, each associated with a different weather phenomenon. Generally,
weather was attributed to the vagaries of the gods, as the wide range of
weather gods in various cultures, for example the Egyptian sun god Ra and Thor,
the Norse god of thunder and lightning, proves. Many ancient civilisations
developed rites such as rain dances and animal sacrifices in order to
propitiate the weather gods.
The ancient Greeks were the
first to develop a more scientific approach to explaining the weather. The work
of the philosopher and scientist Aristotle (384-322 BC) is especially noteworthy,
as it dominated people's views on and their knowledge of the weather for the
next 2000 years. In 340 BC, Aristotle wrote his book Meteorologica,
where he tried to explain the formation of rain, clouds, wind and storms. In
addition, he also described celestial phenomena such as comets and haloes. Many
of his observations were -- in retrospect -- surprisingly accurate. For
example, he believed that heat could cause water to evaporate [47]. But he also
jumped to quite a few wrong conclusions, such as that winds form "as
the Earth exhales" [21], which were rectified from the Renaissance
onwards.
Throughout the Middle Ages
and beyond, the Church was the only official institution that was allowed to
explain the causes of weather, and Aristotle's Meteorologica was established as
Christian dogma [1, p. 7]. Besides, weather observations were passed on in the
form of rhymes, which are now known as weather lore. Many of these proverbs are
based on very good observations and are accurate, as contemporary meteorologists
have discovered [26].
By the end of the
Renaissance, scientists realised that it would be much easier to observe
weather changes if they had instruments to measure fundamental quantities in
the atmosphere such as temperature, pressure and moisture. Until then, the only
tools available were vanes, to determine the wind direction, and early versions
of rain gauges. In 1592, Galileo Galilei (1564-1642) developed the world's
first thermometer. His student Evangelista Torricelli (1608-1647) invented the
barometer in 1643, which allowed people to measure atmospheric pressure. Five
years later, Blaise Pascal (1623-1662) proved that pressure decreases with
altitude. This discovery was verified by Edmond Halley (1656-1742) in 1686;
Halley also was the first one to map trade winds. The discoveries of unknown
continents and, by extension, of unknown climates and weather phenomena also
played a part in the development of modern meteorology [48].
Gradually, scientists began
to understand that weather is influenced by large-scale atmospheric processes
and that wind and storms for example follow certain patterns. One of the first
to study storms was the scientist and politician Benjamin Franklin (1706-1790).
His most famous scientific achievement is his work on electricity and lightning
in particular, but in fact he was very interested in weather and studied it
throughout most of his life. For example, Franklin discovered that storms
generally travel from west to east. Many of Franklin's observations paved the way
to a better understanding of climate and the atmosphere, but
... Franklin was still a natural philosopher at heart, and he was not inclined to clutter his conjectures with a lot of data or mathematics [1, p. 10].
Predicting the weather was
still pigeonholed as a pipe dream and any serious scientist would engage in
studying weather phenomena only in their spare time, if at all. All conjectures
and theories on weather were based solely on observations and it was not until
the early 20th century that mathematics and physics became part of meteorology.
However, by the mid-eighteenth century, governments in various European
countries and in the United States realised that accurate weather forecasts can
considerably help to save money and even lives. Consequently, the first weather
services were established.
2.2)
Establishing Weather Services
One of the first weather
observation networks, which operated from 1654 to 1670, was established by the
Tuscan nobleman Ferdinand II [48]. More than 100 years later, the Palatine
meteorological society (Societas Meteorologica Palatina) installed a first
global weather archive. For fifteen years (1780-1795), 39 weather stations,
spread across Northern America, Europe and Russia, collected meteorological
data three times per day, using standardised equipment [48]. The society did
not produce any forecasts; one of the main obstacles for this was that the data
had to be sent to the society's main office by boat and post coaches, which
took weeks.
The invention of the electrical
telegraph in 1837 by Samuel Morse facilitated the production of weather
forecasts, as data and any other weather observations now could easily and
swiftly be transmitted to another country and even to another continent.
Observation wards began to appear all over Europe and Northern America, but it
was not until the Crimean War (1853-1856) that people realised the benefits of
weather forecasts. The fleet of the Ottoman Empire was surprised by a
low-pressure system and, as a result, lost several ships. The French Emperor
Napoleon III later ordered that the weather for that day should be analysed; he
learned that the storm could have been predicted and that warnings could have
been transmitted by telegraph [12]. Hence, the loss of the ships could have been
prevented.
Meteorologists had begun to
map data from various observation stations, such as temperature and humidity,
onto weather charts (see figure 1). These weather maps enabled the scientists
to detect and study storm systems and wind patterns as well as comparing the
current meteorological situation to past ones, which ultimately led to the
production of forecasts. This method, based on the analysis and comparison of
many standardised observations taken simultaneously, is called synoptic weather
forecasting.
It is still used today
by weather services both as a starting point for and as an addition to
numerical models. Several European governments and later also the US government
realised that timely storm warnings could prevent ship losses. Consequently,
storm-warning systems were installed. The British Meteorological Department
issued regular gale warnings from 1861 onwards; the first US storm-warning
system began to operate ten years later, dwarfing the European services with
its size and funds [33]. These institutions went on to produce general weather
forecasts.
In the 1920s, weather maps
became much more detailed due to the invention of the radiosonde: a small
lightweight box containing measurement equipment and a radio transmitter. It is
attached to a hydrogen-filled weather balloon that can ascend to up to 30 km
before bursting. The radiosonde transmits humidity, pressure, temperature, and
wind speed measurements to a ground station. Of course, radiosondes and weather
balloons have been improved substantially over the last 80 years, but even the
early models allowed meteorologists to observe weather conditions in high
altitudes.
Modern weather services depend on observations transmitted both by radiosondes
and by satellites. The first weather satellite, TIROS 1 (Television and
Infrared Observation Satellite) was launched in 1960. Satellites collect data,
similarly to radiosondes, but they have the great advantage that they can cover
areas difficult to access such as oceans and deserts. Today, both polar
orbiting satellites (at an altitude of 800-900 km; they revolve around the
Earth following the degrees of longitude, passing over both poles) and
geostationary satellites (at an altitude of 35,800 km [48] directly above the
equator; they travel in time with the Earth's rotation, thus constantly
observing the same area) are used.
Still, what improved weather forecasting much more than new observation tools,
was implementing a new forecasting method called numerical weather prediction.
3)
Numerical Weather Prediction
Both the financial
significance of weather forecasts and the necessity of knowing more about
atmospheric processes were understood fairly soon after the first gale warnings
were published, but very few people realised that mathematics could be used to
describe these processes and produce more accurate forecasts than synoptic
meteorology ever could. In the early 20th century, scientists, in particular
Vilhelm Bjerknes and Lewis Fry Richardson, pioneered numerical weather
forecasting, which is based on applying physical laws to the atmosphere and solving
mathematical equations associated to these laws. The discovery of chaos theory
and not least the development of computers greatly improved the quality of
forecasts. Today, meteorologists constantly refine the various forecasting
models designed by the world's leading weather services.
3.1) Finding the Maths
The first mathematician who thought of applying mathematics to weather
forecasting was the Norwegian Vilhelm Bjerknes (1862-1951). Already at a young
age, Bjerknes engaged in mathematics as he assisted his father with his
research in hydrodynamics. He then studied mathematics and physics at the
University of Christiania (nowadays Oslo). In 1898 he formulated his
circulation theorem: in a nutshell, it explains the evolution and the subsequent
decay of circulations in fluids. Possibly even more importantly, the theorem
also marks "the move of Vilhelm Bjerknes into meteorology"
[11, p. 479]. Combining his circulation theorem with hydrodynamics and
thermodynamics, Bjerknes discovered that, given initial atmospheric conditions,
it is possible to compute the future state of the atmosphere using mathematical
formulae. As he put it himself [1, p. 152]:
We must apply the equations of theoretical physics not to ideal cases only, but to the actual existing atmospheric conditions as they are revealed by modern observations. ...From [these] conditions ... we must learn to compute those that will follow.
During a visit to the
United States in 1905, he presented his theories. The Carnegie Foundation was
so impressed by his ideas that it funded Bjerknes's research for the next 36
years. Bjerknes founded the Bergen Geophysical Institute, also known as the
Bergen School, which would make several important contributions to modern
meteorology. Together with his son Jacob, who became a famous meteorologist
himself, and meteorologists Tor Bergeron and Halvor Solberg, he discovered that
weather patterns are closely associated with so-called fronts, i.e. transition
zones between warm and cold air masses, and described the life cycle of
mid-latitude cyclones. Most of Bjerknes's important results were published in On
the Dynamics of the Circular Vortex with Applications to the Atmosphere and to
Atmospheric Vortex Wave Motion in 1921.
Bjerknes' equations were
very complicated and not very practical for predicting the weather as they
required immense computational power, a fact of which he was aware himself.
Nevertheless, he firmly believed that one day, meteorology would be a proper
science and weather forecasts based on solving mathematical equations would be
feasible:
It could take years to drill a tunnel through a mountain. Many a worker will not live to witness the breakthrough. Nonetheless, this will not bar others from later riding through the tunnel at express train speed. [27]
The first attempt to use
mathematics in order to predict the weather was made by the British
mathematician Lewis Fry Richardson (1881-1953), who simplified Bjerknes'
equations so that solving them became more feasible. Richardson, who had studied
a number of sciences at both Newcastle University and the University of
Cambridge, worked in the British Meteorological Office from 1913 until 1916. In
1919, he resumed his former job there, but resigned only a year later when the
Meteorological Office became part of the Air Ministry. Richardson would have
needed to join the army, which was incompatible with his pacifist Quaker
conviction.
He also worked for the
National Peat Industries for some time, and in order to solve differential
equations modelling the flow of water in peat, he invented his method for
finite differences, which produces highly accurate results. Basically, this
method allows finding approximate solutions to differential equations. A
differential equation with a smooth variable is converted into a function (or
an approximation thereof) that relates the changes of the variable and given
steps in time and/or space, meaning that the changes are calculated at discrete
points rather than at infinitely many points. Then the derivatives in the
differential equation are replaced by finite difference approximations (this
method will be explained in more detail in section 4.1). So in the place of the
differential equation you get many equations which can be solved using
arithmetic.
Finite difference methods
are widely used nowadays, but in Richardson's days, other mathematicians
considered the method to be "approximate mathematics" [8, p.
xvi]. Nevertheless, when Richardson came across problems of the dynamics of the
atmosphere at his work at the Meteorological Office, he decided to solve them
using his method. He remodelled the fundamental equations describing
atmospheric processes such that it was possible to solve them numerically.
By dividing the surface of the Earth into thousands of grid squares, and the
atmosphere into several horizontal layers, he obtained a large number of grid
boxes, connected to one another by mathematical equations. Fundamentally,
Richardson applied Bjerknes' vision of calculating the future state of the
atmosphere using observations of its current state to the grid and added to it
the idea that there is a connection between the grid boxes.
Richardson imagined a "forecast
factory" where thousands of human computers would be seated on galleries
along the walls of a huge hall. Each computer would be responsible for
calculating the changes in the atmosphere for discrete points in one grid box.
In the centre of the room, there was to be a pulpit with a
"conductor" who would make sure that the computers all worked at
uniform speed, in time with each other. The calculations would be collected as
soon as they were finished in order to be transmitted to a radio station. Richardson
also included a research department in charge of refining the models [10; 1,
pp. 157-158].
This forecast factory is
"remarkably similar to descriptions of modern multiple-processor
supercomputers used in weather forecasting today" [10]. In Richardson's
days, however, all the computations had to be done manually, and he estimated
that his factory would need 64,000 human computers to master the mammoth task
of calculating the weather in time with the weather actually happening. But he
believed that:
Perhaps some day in the dim future it will be possible to advance the computations faster than the weather advances and at a cost less than the saving to mankind due to the information gained. But that is a dream. [1, p. 161]
In 1916, Richardson decided
to join the Friends Ambulance Unit (that had been formed for conscientious
objectors) and serve in the First World War, out of curiosity. He took his
research with him, and when he was not transporting wounded to military
hospitals, he tested his model. For this he used data collected on 20th May
1910, which had been an international balloon day where European observatories
had taken measurements in the upper air, and that were provided by Vilhelm
Bjerknes. It took Richardson weeks to produce a six-hour forecast, and when he
compared his results to the actual measurements, he discovered that his results
were not only highly inaccurate, but also absolutely unrealistic. Nonetheless,
he decided to include his calculations in his seminal book Weather
Prediction by Numerical Process, which was published in 1922. For him, this
first failed attempt to put his model into practice was only a minor detail
compared to the fact that he had developed his method in the first place. [1,
p. 160]
Very few understood the importance
and the novelty of Richardson's work at the time, as, as he wrote himself,
"the scheme is complicated because the atmosphere is complicated"
[1, p. 161]. This lack of recognition and the affiliation of the Meteorological
Office to the Air Ministry led Richardson to abandon meteorology. He spent a
considerable amount of the rest of his life studying the mathematics of war.
Richardson's theories were
not put into practice again until the mid-1940s, when a team of scientists at
the Institute for Advanced Study in Princeton developed the world's first
computers. Meanwhile, the groundbreaking research of meteorologists such as
Jacob Bjerknes (1897-1975) and Carl-Gustaf Rossby (1898-1957) furthered
scientists' knowledge of the atmosphere and helped pave the way for the
eventual triumph of numerical weather forecasting.
Rossby in particular should
be credited with this, as he almost single-handedly changed the practices of
the U.S. Weather Bureau, introducing forecasting methods based on
meteorological and physical theories. Before moving to the United States,
Rossby had worked at the Bergen Geophysical Institute under Vilhelm Bjerknes.
He brought the school of thought of the Bergen scientists across the pond,
where he established several meteorological centres. Apart from training young
meteorologists, Rossby produced stunning research results. In 1939, when he
held a professorship at the Massachusetts Institute of Technology (MIT), he
discovered the so-called Rossby waves, which are meanders of large-scale
airflows in the atmosphere. They form when an airflow, for example the jet
stream, is deflected either to the north or to the south (by a mountain range
for example), but because of the conservation of "potential
vorticity", the flow returns to its original latitude. Rossby waves are
very long, with only three to six oscillations around the entire planet; they
play a very important role in the formation of cyclones (i.e. lows) and
anticyclones (i.e. highs) [2, p. 216].
The wave speed c
relative to the ground is given by:
where U is the mean
westerly wind, ω is the angular velocity of the Earth, φ is the latitude, RE
is the radius of the Earth and λ is the wavelength [46; 4, p. 237]. The middle
term on the right-hand side is the so-called Rossby parameter, which describes
the variations of the Coriolis parameter with latitude, where the Coriolis
parameter fC is given by:
fC = 2 × ω × sin φ
Calculating the wave speed
gives the movement of the wave crests from west to east [4, p. 237]. In terms
of numerical weather prediction, this equation is important as it facilitated
extended five-day forecasts [1, p. 186].
The work of Vilhelm Bjerknes
and Richardson had divided the meteorological world into two camps: one camp
defended the old method of comparing the current state of the atmosphere with
past observations; the other camp campaigned for the use of physics in weather
forecasting.
A turning point was the 6th
of June 1944: D-Day. For the invasion of Normandy to be a success, the
commanders of the Allied forces wanted certain weather conditions (clear enough
skies, relatively calm winds). Their requirements for the tide and the moon phase
restrained the time span in which to undertake the invasion to early June; the
exact day should be determined on the basis of weather forecasts. The
commanders had employed advocators of the two opposing schools of thought in
weather forecasting: the Norwegian meteorologist Sverre Petterssen, a disciple
of the Bergen School, and the American Irving Krick, whose reputation as a
forecaster mainly stemmed from his talent for selling himself. Throughout May
1944, the weather had been calm, and Krick, having studied old weather maps,
predicted that the conditions would not change. Meanwhile, Petterssen saw heavy
storms coming in from the Atlantic. The only day with conditions good enough
for the invasion was 6th June [10; 1, pp. 189-195]. The commanders decided to
trust Petterssen's forecast, thereby demonstrating a great deal of trust in
science [1, pp. 195-196].
D-Day not only changed
world history, it also highlighted the importance of weather forecasts [10].
Soon after the Second World War, American scientists used the world's first
computers to predict the weather. Other groundbreaking research results, be it
the formulation of chaos theory, be it the invention of computers,
significantly changed weather forecasting. Thus, numerical weather prediction began
to conquer the world.
3.2)
Chaos and Computers
The mathematician John von
Neumann (1903-1957), one of the fathers of computer science, was the first one
to think of using computers to predict the weather. His major motive was not
meteorology, though, as he thought that by predicting the weather, one might be
able to control it and use it as a weapon. In 1946, he presented his ideas to a
group of leading meteorologists, including Carl-Gustaf Rossby and the young,
gifted mathematician Jule Charney (1917-1981).
Charney became one of the leading scientists in von Neumann's Meteorology
Project at the Institute for Advanced Study in Princeton. The team developed
their own computer, but ended up using the ENIAC (Electronic Numerical
Integrator and Computer), which belonged to the U.S. Army, for their first
forecast because their computer was not yet ready. In 1950, the ENIAC
successfully produced a 24-hour forecast. This took about 24 hours, but the
computer developed by von Neumann's team was much faster (this computer
produced its first forecast in 1952), and from 1955 onwards, numerical
forecasts generated by computers were issued on a regular basis. At first,
experienced human forecasters were sceptical about the quality of these
forecasts, which admittedly were not as good as forecasts made by humans, but
the rapid development of computers and hence their speed dramatically improved
forecast quality.
The prerequisite for
computer-generated forecasts was to simplify the full primitive equations that govern
the atmosphere (they will be discussed in section 3.3), as the early computers
were unable to deal with all the equations included in Richardson's model. In
1948, Charney developed the quasi-geostrophic approximation, which reduces
several equations of atmospheric motions to only two equations in two unknown
variables [14, chapter 13]. These equations are much easier to solve and could
be handled by the early computers. (Geostrophic winds are hypothetical winds
for which the balance between the pressure-gradient force and the Coriolis
effect is exact (see section 3.3) [2, p. 112]. In Charney's approximation,
winds are assumed to be almost geostrophic.)
Furthermore, this
approximation filters out all but the slow long-wave motions that are important
in meteorology, so that you do not have to solve the primitive equations for
acoustic and gravity waves as Richardson did 30 years earlier. Although the
computers were fed with simplified equations only, the limited computer power
demanded a barotropic (i.e. single-layer) model of the atmosphere. Further
research, both in meteorology and in computer science, finally allowed the
application of baroclinic (i.e. multi-layer) models. In 1963, a six-layer model
based on the primitive equations was used for producing a forecast. Since then,
as computer power increased, the models have constantly been refined (meaning
that more layers, a finer grid, more equations, topography and landscape
characteristics were included) [4, p. 314]. This dramatically increased both the
forecast accuracy and quality.
Today, the world's leading
meteorological centres use the most powerful computers on the planet; the new
computer at the British Met Office for example is capable of 125 trillion
calculations per second [42].
Meteorologists were thrilled by the possibilities that seemed to open up due
the use of computers in weather forecasting, and were convinced that it would
only be a matter of time before man could not only accurately predict, but also
control the weather. The discovery that the atmosphere is chaotic, by MIT
researcher Edward Lorenz (1917-2008) in 1961, came as a serious blow to all
these high-flying ideas. As opposed to other meteorologists at the time, Lorenz
did not predict the weather, but investigated how predictable it is, in other
words, if there are periodic patterns (the existence of patterns would have
supported the belief of some old-school meteorologists that weather forecasting
based on the study of past weather events yields accurate results). For this he
ran a shortened forecasting model on his computer, and to his great surprise,
inputting data that differed from previously entered values only in the fourth
decimal place, significantly changed the weather the computer predicted [38].
Lorenz reasoned that the dynamical equations that describe the atmosphere are
exceedingly sensitive to initial conditions. Dynamical equations are
deterministic; meaning that given initial conditions, they determine how the
process they describe will evolve in the future. But, in the case of the
atmosphere (and many other systems as well, chaotic behaviour can be found in
every branch of science), you need to enter the exact same data as initial
conditions in order to get the same results if you run the model several times.
Even seemingly minuscule differences in the initial conditions result in highly
different outcomes. A very simplified example for chaotic behaviour is the
trajectory of a paper aeroplane: Imagine you throw a paper aeroplane in a
similar manner and in the same direction say ten times. Every time, the
trajectory of the plane will be different, because you will never be able to
throw the plane in the exact same manner twice: the force you exert or the way
you hold the plane in your hand when throwing it will differ ever so slightly
from throw to throw, resulting in very different, unpredictable flights.
Chaotic behaviour is
commonly known as the "butterfly effect", a term coined due to the
title of a talk Lorenz gave in 1972: Predictability: Does the Flap of a Butterfly's
Wings in Brazil Set Off a Tornado in Texas? Meteorologists had presumed
that small weather changes in some specified places would affect the weather in
other places, but after Lorenz's discovery, they had to accept that it did not
matter if a butterfly flapped its wings in Brazil, or Bulgaria, or Bangladesh,
the result might still be a tornado in Texas (or somewhere else for that
matter). This, combined with the fact that observations of the atmosphere are
usually slightly erroneous, meant that long-range forecasts would not be
possible, as the small errors would build up very quickly and change the
outcome considerably. Lorenz believed that weather could not be forecast
accurately for more than about two weeks. The current models do not even exhaust
this limit, as:
After about ten days it is essentially impossible to forecast weather with any degree of accuracy. [22]
Modern forecast models
allow for the chaotic nature of the atmosphere by a process called ensemble
forecasting, meaning that the model is run several times, each time with
slightly different initial conditions. The results are then averaged out to
give a forecast. This method can also suggest unlikely weather conditions with
quite a high degree of accuracy [4, p. 330].
Finding a balance between
detailed, accurate long-range forecasts and chaotic behaviour is still a part
of modern meteorological research. But before looking at current forecasting
models, let us look at the primitive equations that form the basis of every
such model.
3.3)
Primitive Equations
For each weather forecast,
meteorologists need to know the values of seven physical quantities:
temperature, pressure, density, humidity, and wind velocity, containing three
components accounting for the three different wind directions. Some forecasting
models also include the content of water and ice in clouds and at the ground.
Ideally, these values would be known at every point in the atmosphere at any
time. This is virtually impossible due to limited computational power,
therefore the atmosphere is divided into many small air parcels, and the values
are calculated for each parcel. Scientists treat the Earth's atmosphere as if
it were a fluid on a rotating sphere in order to describe large-scale
atmospheric processes using the fundamental laws of thermodynamics and
hydrodynamics, also called the primitive equations. Essentially, they are the
equations of motion, one for each of the three wind directions, the continuity
equation, describing the conservation of mass, the ideal gas law, and the first
law of thermodynamics, describing the conservation of energy. There is also an
equation for determining the humidity, which is not always included in the set
of the primitive equations (and is not treated here). Furthermore, the following
forces have to be taken into account: gravitation, drag force, pressure
gradient force, and, since the Earth is rotating, the Coriolis and the
centrifugal forces [15, p. 118]. Here, only the very basic versions of the
primitive equations are described.
The equations of motion are
based on Newton's second law 
: force equals the product of mass and
acceleration. Basically, they describe how an object moves under different
circumstances. The movement of an air parcel, i.e. the winds in a parcel, is
predicted by
where 
indicates the change of velocity 
with respect to the time t. The terms on
the right-hand side represent the forces acting in the atmosphere, namely the
pressure gradient force, the Coriolis force, the drag force and the
gravitational force.
The pressure gradient force
(per unit mass) 
is perpendicular to the isobars
(lines on weather charts joining points where the atmospheric pressure is the
same [2, p. 142]) and is given by
with ñ being the density and p being the pressure. The symbol ∇ is called Nabla and is a vector differential operator. Depending on the
domain in which it is applied, it denotes various quantities, for example the
gradient of a scalar field, or the divergence of a vector field.
The Coriolis force 
can be regarded as the difference between
centrifugal force and gravitation [4, p. 184]. Because of the Earth's rotation,
air moving above the planet is deflected sideways, forced to follow a curved
path. In the Northern hemisphere, air is deflected to the right of its
direction of motion; in the Southern hemisphere, it turns to the left. The
Coriolis force accelerates wind in the horizontal; it is highest at the poles
and zero at the equator due to the Earth's nearly spherical shape. In
mathematical terms, it is
with 
being the angular velocity of a rotating system
(here of the Earth) and being the velocity of an object
relative to the system.
The air in the boundary
layer, i.e. in the "air belt" of 1-2 km altitude above the Earth's
surface, is exposed to drag against the ground. The drag force 
increases with wind speed, but acts against the
wind direction, thereby decelerating the wind.
The term represents the gravitational force.
Thus, the equation of
motion can be rewritten as
Customarily, dynamical
processes in the atmosphere are described in an orthogonal coordinate system
rotating in time with the Earth. Therefore spherical coordinates are used.
The three components of
wind velocity are written as follows:
Here, u is the zonal
wind, parallel to the circles of latitude; v is the meridional wind,
parallel to the circles of longitude; and w is the vertical wind
component [16]. The latitude is denoted by φ (-π/2 < φ < π/2), the longitude by λ (-π < λ < π) and the height above the Earth's surface by z.
Their changes with respect to time are indicated by 
, 
and 
respectively. The distance between the air
parcel and the geocentre is given by r, where r = RE
+ z (RE being the Earth's radius). Often, this
distance is approximated by the Earth's radius, so 
. In the following formulae, I will use r
for better legibility.
In many forecasting models,
hydrostatic equilibrium is assumed, meaning that the gravitational and the
pressure gradient forces are balanced. For the vertical component of velocity w
we then have 
.
Then the equations of
motion in spherical coordinates are:
where Fλ and Fφ are components of frictional force.
For predicting the motion of winds at discrete points, a so-called Eulerian
reference frame is used. In this frame, the time rate of change of any quantity
is expressed by
The Nabla operator can also
be expressed in spherical coordinates as
where 
are the normalised unit vectors for the
directions λ,
φ and z,
respectively.
The basic principle
underlying the continuity equation is the conservation of mass. Fundamentally,
matter can be neither created out of thin air nor can it be destroyed
completely; but it can be rearranged. If you want to build a house, for
example, you have to use material that has already existed in some form, but
through the building process it becomes a house. And if you burn a tree trunk,
the wood does not vanish completely as ashes will always remain. The situation
is similar for the atmosphere; if the atmospheric pressure rises in one place,
it has to decrease in some other place so as to guarantee the balance. This
means that if you subtract the mass flowing out of an air parcel from the mass
that flew in, you obtain the change of mass within the parcel [4, p. 196]. The
continuity equation is used to determine the air density.
In the Eulerian reference
frame, the continuity equation is
This can be approximated
(filtering weak acoustic waves) by
where ñ0(z)
is the base-state density, an exponentially decreasing function of height.
Substituting the continuity equation by the above filter condition is called
anelastic approximation [6, p. 7].
The pressure in an air
parcel is found using the equation of state, which relates pressure,
temperature and density. Air behaves similar to a perfect gas, so the ideal gas
law for perfect gases can be used to determine atmospheric pressure p:
Here, T denotes the
absolute temperature (in Kelvin); and 
is the gas constant for dry air with
. The gas constant is different for moist air,
as water vapour is less dense than dry air. But instead of using a different
gas constant, a virtual temperature defining this effect can be used.
In order to determine the
temperature in an air parcel, forecasters make use of the first law of
thermodynamics. This law expresses the conservation of energy, or heat, as heat
is a form of energy. In essence, energy cannot be created or destroyed (similar
to mass), but it can change forms. For example, if you have a bonfire, you need
to input energy in the form of wood, and energy is released in the form of heat
and light. The first law of thermodynamics also states that the amount of
energy added to a system cannot be bigger than the amount of energy released
from the system, in other words, the amount of energy supplied is exactly
balanced by the work done (within the system).
In terms of the atmosphere,
the conservation of energy means that the temperature in an air parcel changes
only when heat is added or removed. This can be caused by warmer or cooler air
moving into the parcel, or by evaporation (which cools the air) or condensation
(which releases heat). Furthermore, the temperature in a parcel can change if
the parcel moves about vertically. This property is very important for the
formation of clouds [4, p. 45].
The equation describing the
change of temperature T with respect to time t is:
Here, cp
is the specific heat of air, with constant pressure, and 
is the diabatic rate of latent heat release per
unit mass. The term latent heat means hidden heat, and describes the amount of
energy released or absorbed by a substance -- water, in the case of the
atmosphere -- during a change of state of that substance. Latent heat is
released during condensation and fusion, for example; and is absorbed during
evaporation and melting. "Diabatic" means that heat is transferred.
The other processes in the equation are adiabatic, meaning that there is no
heat transfer.
The
primitive equations were first used in a weather forecast by Lewis Fry
Richardson. Jule Charney and his colleagues had simplified them so that the
early computers could handle them, but nowadays meteorologists have gone back
to use all of Richardson's equations.
All current weather
forecasting models are based on the primitive equations -- or versions thereof
-- but each model uses different approximations and assumptions, resulting in
slightly different outcomes. Also, the models include equations accounting for
the effects of small-scale processes such as convection, radiation, turbulence
and the effects of mountains that cannot be represented explicitly by the
forecasting models, as their resolution is not high enough. This process is
called parameterisation.
Furthermore, before weather
data gathered from various observations can be entered into the computer
models, they have to be assimilated. During data assimilation, real
observations are combined with predicted conditions so as to give the best
possible estimate of the actual state of the atmosphere. This process is
necessary, as inputting raw data obtained just from observations results in
inaccurate forecasts [4, p. 318].
Assuming that hydrostatic
balance applies limits the smallest possible grid spacing to about 5 - 10 km
[29], which is not fine enough a resolution for detailed, accurate forecasts of
small-scale weather events like thunderstorms.
Some models, such as the
regional model COSMO developed by the German weather service Deutscher
Wetterdienst (DWD), have therefore abandoned this assumption and are based on
non-hydrostatic thermodynamic equations (similar to the equations used in fluid
mechanics). This permits a much finer resolution (i.e. smaller grid spacing),
but as a result, the primitive equations are much more complex and
computationally more demanding as vertical wind components are included in the
model [29].
Moreover, in order to improve the model's forecast accuracy and quality, the
vertical coordinate z can be replaced by the generalised vertical
coordinate ζ,
allowing the orthogonal spherical coordinate system to be transformed into a
terrain-following coordinate system, which is conformal to the Earth's
orography (coordinate systems will be presented in chapter 4). Again, the
primitive equations have to be re-written in terms of ζ [6, pp. 31-32].
Not all forecasting models
have such a coordinate system, though; there are several grid models. But let
us now look at the methods employed by meteorologists to solve these equations.
4)
Forecasting Models Used Today
For his forecasting model,
Richardson constructed a grid to divide the atmosphere into many small air
parcels. In essence, this is still done by meteorologists today, but several
different grid versions have been developed. Similarly, Richardson's finite
difference method is not the only method for solving the primitive equations anymore;
its strongest "opponent" is the so-called spectral method, which will
be described in section 4.2. A third method, the finite element method, will be
presented briefly in section 4.3.
Before the primitive
equations can be solved, they have to be discretized with respect to space and
time. Discretization means that the atmosphere (or the part of it that you want
to study) is represented by a finite number of numerically approximated values.
The most common numerical
time integration scheme in meteorology is the leapfrog scheme. In order to make
a forecast for the future (at time step t + Δt), you do not start at the present time step t,
but at the previous step t - Δt, and the forecast leaps over the time step t (with Δt denoting the size of the time step, that is
the difference between two points in time). The scheme is applied both in the
finite difference method and in the spectral method.
All
the different methods need to be stable, in other words, it has to be
guaranteed that the numerical solution does not diverge from the true solution
as the time span for which the forecast is made increases. There are various
stability criteria for atmospheric processes such as advection and wave
propagation. One of the main causes for instability are truncation errors,
which happen when a variable ψ is represented by a Taylor series, i.e. as an
infinite sum of its values at the individual grid points. Due to computational
reasons, only the very first terms of the series, which are in fact the most
important ones, can be used, but the higher-order terms influence the accuracy
of the series. As a second order scheme, the leapfrog scheme is fairly
accurate; an even better scheme is the so-called Runge-Kutta method, which is
of fourth order (but it will not be described here). However in most of the
current models only second order schemes can be applied due to computer
capacities.
The accuracy of all forecasting models is tested regularly; statistical models
have been developed for this.
The mathematical
methods described in the subsequent sections are based on notes published by
the European Centre for Medium-Range Weather Forecasts (ECMWF) in Reading, and
by the German weather service DWD.
4.1)
The Finite Difference Method
The
traditional grid structure is based on dividing the Earth's surface into a
large number of squares, such that there is a high air column above each
square, as illustrated in figure 6. The atmosphere is then divided into a
number of layers, resulting in a three-dimensional grid, in which the primitive
equations can be solved for each grid point. In general, the layers are much
thinner close to the Earth's surface than the layers in the upper atmosphere,
as most weather events happen relatively close to the ground. Processes in the
upper atmosphere influence the weather, though, so the whole of the atmosphere
has to be considered in a forecasting model. Most models also include several
subterranean layers so as to take the air and water exchange between atmosphere
and ground into account. Over the years, the resolution of the grids has become
higher (i.e. the edge length of each square has become smaller).
The world's leading weather
services such as the British Met Office and the German DWD use three different
grids: a global grid spanning the whole planet, a so-called regional model
covering Europe (and North America in the case of the Met Office's model), and
a local model covering the UK or Germany, respectively. The regional model of
the DWD has a resolution of 7 km, and the local model has a resolution of up to
2.8 km (the Met Office's models have coarser resolution as the Met Office does
not work with non-hydrostatic equations). Both of these local models, and all
of the Met Office models, are based on a rectangular grid, whereas the DWD's
global model is based on a triangular grid with a 40 km resolution (see figure
7). The great advantage of the triangular grid is that the primitive equations can
be solved in air parcels close to the poles without any problems, as opposed to
the rectangular grid, where the longitudes approach each other, resulting in
erroneous computations.
Generally, in a
terrain-following coordinate system, the grid-spacing in the
λ-direction is given by Δλ; similarly,
Δφ and
Δζ represent the spacing in the φ-direction and the ζ-direction, respectively. As in
section 3.3, λ denotes the longitude, φ denotes the latitude and ζ is the height coordinate. The
position of the grid points in the computational space is defined by
Here, Nα is the number of grid points in the
α-direction;
λ0 and φ0 are the values of λ and φ in the southwest corner of
the model domain [6, p. 53].
Now, the primitive
equations have to be re-written in finite difference form. For this, we need to
define approximations to the derivatives at a specified grid point xl
in terms of finite differences. The value of a variable ψ at xl is given by
ψl; and the finite difference for ψl is given using the values of ψl+1 and ψl-1, i.e. the values at the two adjacent grid
points. The behaviour of these two terms can be described using Taylor
expansion:
Subtracting the second from
the first expansion gives the centred finite difference approximation to the
first derivative of ψl:
The term 
gives the truncation error and can be omitted
since it is small. However, the lowest power of the difference of x, Δx, in E gives the order of the
approximation. So this scheme has order 2. As mentioned above, the higher the order,
the more accurate the approximation. In general, centred finite difference
approximations are better than forward or backward approximations, which can
also be derived from the Taylor expansions for ψl+1 and ψl-1.
Solving the first expansion
for ψ'l
gives the forward approximation:
Similarly, the backward
approximation is derived from the second expansion:
These schemes both have
order 1, but there are situations where it is favourable to use these approximations
instead of a centred approximation. It is also possible to derive the finite
difference approximations to the second and third derivatives of ψl.
Not only space, but also
time has to be discretized, and time derivatives can also be represented as
finite difference approximations, that is in terms of values at discrete time
levels [17, p. 15]. A time step is denoted by Δt, and a discrete time level is given by tn = t0
+nΔt with t0 being the
initial time for integration. The grid point value of the variable ψl at time step tn is denoted
by ψnl; its derivative can be expressed as a centred
finite difference approximation:
Again, O represents
the truncation error and can be omitted.
There are two different
finite difference schemes: the explicit scheme and the implicit scheme. The
explicit scheme is much easier to solve than the implicit one, as it is
possible to compute the new value of ψl at time n+1 for every grid point,
provided the values of ψl are known for every grid point at the current
time step n [17, p. 15]. But the choice of the time step is limited in
order to keep the scheme stable. The implicit scheme, on the other hand, is
absolutely stable, but it results in a system of simultaneous equations, so is
more difficult to solve [17, p. 27]. Both explicit and implicit schemes are
used in current forecasting models.
The approximations
described above are very simple examples illustrating the general idea of
finite differences. When the primitive equations are expressed in terms of
finite differences, the equations soon become very long and take some
computational effort to solve. Explicit time integration can be made more
efficient, though, by implementing a so-called mode-splitting technique. This
means that the primitive equations are subdivided into forcing terms fψ referring to slowly varying modes
and source terms sψ directly related to the fast-moving sound
waves: 
. The terms fψ are integrated over big time steps
Δt. These
time steps are then subdivided into several small time steps Δτ, over which the terms sψ are integrated [6, pp. 61-64].
In the case that sψ = 0, we get, using a 2Δt leapfrog interval,
representing a set of
equations that can be solved using Gaussian elimination [6, p. 63].
For equations including
acoustically active terms, i.e. where acoustic and gravity waves have to be
taken into account, the finite difference is given by
The superscript m is
the time step counter for the integration over the small time steps Δτ within the leapfrog interval used
above.
The term f nψ is constant throughout the small
time step integrations, but the value of ψn+1 is not known before the last one of these
integrations has been completed. Therefore, the finite difference for f nψ has to be re-written as
The term 
is the result of a process called averaging;
you assume that the mean value of ψn+1 does not vary as fast with respect to both
space and time than deviations from the mean would. The notation for
averaging is
with a being an
integer. The notation is similar for the longitude λ.
If you re-write the
primitive equations using finite differences, you get, "after
considerable algebra" [6, p. 67], a linear tridiagonal system of
simultaneous equations which can be written in the general form
The terms Ak,
Bk and Ck are matrix diagonals, whereas Dk
is an inhomogeneous term including the appropriate boundary conditions. The
equation system can be solved for using a solving method based on
Gaussian elimination and back-substitution.
In a nutshell, the
derivatives in the primitive equations can be approximated by finite differences,
such that the equations can be transformed into a linear equation system. It
takes modern supercomputers at the leading weather services quite a while to
solve all these equations, so it is astonishing that Richardson managed to
produce a numerical weather forecast at all, even if it was for a limited area.
However, the application of this method to the primitive equations was crucial
to the development of numerical weather forecasting, as it was the only
mathematical method that could simplify partial differential equations needed
for forecasting for several decades.
A further disadvantage of
the finite difference method, other than the great number of equations you have
to solve, is that it does not reveal anything about the behaviour of the
variables between the individual grid points. The spectral method, on the other
hand, takes this into account.
4.2) The Spectral Method
The spectral method was
already devised in the 1950s, but it took a while before the method was
implemented in forecasting models. In 1976, the Australian and Canadian weather
services were the first ones to adopt this method, which is now used by a range
of weather services across the globe; the European Forecasting Centre ECMWF in
Reading, for example, adopted it in 1983 [20]. One of the advantages of the
spectral method is that the primitive equations can be solved in terms of
global functions rather than in terms of approximations at specific points as
in the finite difference method. For the ECMWF, this is the better option as
they require a global model in order to produce medium-range weather forecasts.
For the spectral method,
the atmosphere has to be represented in terms of spectral components. In the
ECMWF model, the atmosphere is divided into 91 layers (in comparison, the DWD's
and the Met Office's global models have 40 layers), with the number of layers
in the boundary layer equalling the number of layers in the uppermost 45 km of
the atmosphere. The partial differential equations are represented in terms of
spherical harmonics, which are truncated at a total wave number of 799. This
corresponds to a grid length of roughly 25 km [7] (the DWD's and the Met
Office's global model has a resolution of 40 km).
In essence, in using the
spectral method, you assume that an unknown variable ψ can be approximated in terms of a
sum of N+1 linearly dependent basis functions ψn(x):
When this series is
substituted into an equation of the form Lψ = f (x), where L
is a differential operator, you get a so-called residual function:
R(x: a0, a1, ... , aN) = LψN - f
The residual function is
zero when the solution of the equation above is exact, therefore the series
coefficients an should be chosen such that the residual
function is minimised, i.e. that it is as close to zero as possible. In the
majority of cases, polynomial approximations, such as Fourier series or
Chebyshev polynomials, are the best choice; but when it comes to weather
forecasting, the use of spherical coordinates demands that spherical harmonics
are used as expansion functions. This increases the complexity of the problem,
and the computational effort required to solve it.
A simple example that can
be solved in terms of a Fourier series illustrates the idea of the spectral
method: One of the processes described by the primitive equations is advection
(which is the transport of for instance heat in the atmosphere), and the
non-linear advection equation is given by
This can be re-written in
terms of the longitude λ:
Having chosen appropriate
boundary conditions, the equation can be expanded in terms of a finite Fourier
series:
where the um are the complex expansion coefficients and M is the maximum wave number [17, p. 61]. The advection equation then is:
where Fm
is a series in terms of the um.
As each of the terms on the left-hand side of the equation has been truncated
at a different wave number, there will always be a residual function. There are
several methods which convert differential equations to discrete problems, for
example the least-square method or the Galerkin method, and which can be used
in order to choose the time derivative such that the residual function is as
close to zero as possible [17, p. 63].
It is difficult to
calculate the non-linear terms of a differential equation in the context of the
spectral method, but you can get around this problem by using a so-called
transform method. Most commonly, Fast Fourier Transforms are used, but in
principle all transform methods make it possible to switch between a spectral
representation and a grid-point representation [17, p. 64]. Using a transform
method requires three steps, which will be shown for the non-linear term 
in the advection equation above:
Firstly, the individual
components of the non-linear term u and 
are expressed in terms of spectral coefficients
at discrete grid points λi:
Secondly, the advection
term, that is the product of these components, is calculated at every grid
point in the discretizised space:
Then you can return to the
spectral space and calculate the Fourier coefficients:
This procedure has to be
done at every time level, so results in a significant amount of calculation.
Furthermore, products with more than two components suffer from aliasing,
meaning that waves that are too short to be resolved for a certain grid
resolution falsely appear as longer waves [17, p. 37]. Still, using transform
methods is necessary in order to solve differential equations in spectral space.
As has been mentioned
above, a dependent variable ψ has to be expanded in terms of spherical
harmonics rather than Fourier coefficients when spherical coordinates are used.
Spherical harmonics Ynm(λ, φ) are the angular part of the
solution to Laplace's equation. The vertical components of velocity 
transform like scalars, so can be expanded in
terms of spherical harmonics straightaway. It is slightly more complicated for
the horizontal components 
and 
:
[5, p. 395] with the spherical harmonics
where m and n
are non-negative integers such that n ≥ m [5, p. 399].
Here, m is the zonal wave number, and n is the total wave number.
The term Pnm(φ) is the associated Legendre function used in
spherical harmonics (but will not be explained here).
Expansion in terms of
spherical harmonics requires transform methods as well, but these methods are
more complicated and computationally more expensive than Fast Fourier
Transforms (although the use of transform methods greatly reduces the time
required for calculations).
Spherical harmonics are
two-dimensional, so they are much more difficult to solve than expansions in
terms of Fourier series. But:
... there is no way to solve problems on the sphere that does not require some complicated programming and careful attention to detail. [5, p. 399]
In general, spectral method
algorithms are more difficult to program than their finite difference
counterparts; also the domains in which they are used have to be regular in
order to keep the high accuracy of this method. However, the spectral method
has a number of advantages: for example, there is no pole problem when the
method is used. At the poles, the solutions to differential equations become
infinitely differentiable; therefore the poles are usually excluded from the
spectral space, which actually simplifies the method [5, p. 383]. Furthermore,
it can handle finite elements of higher orders than the finite difference
method can. As a result, the solutions of many problems are very accurate. The
high accuracy also results in the fact that the models do not need as many grid
points as in the finite difference method, and computers on which the method is
run require less memory space.
Summing up, the spectral
method gives much more accurate results than the finite difference method. Many
weather services still use the finite difference method though because it is
much easier to implement and because "the physics is so complicated ...
that purely numerical errors are a low priority." [5, p. 17]
4.3)
The Finite Element Method
A third technique for
finding approximate solutions to partial differential equations and hence to
the primitive equations is the finite element method. It is quite similar to
the spectral method in that a dependent variable ψ is defined over the whole domain in
question, rather than at discrete grid points used in the finite difference
method. Moreover, a finite series expansion in terms of linearly independent
functions approximates the variation of ψ within a specified element (e.g. a set of grid
points) [17, p. 75]. Unlike the spectral method, the basis functions are not
globally, but only locally non-zero; also they are low-order polynomials rather
than high-order polynomials. The domain for which the partial differential
equations have to be solved is divided into a number of subdomains, and a
different polynomial is used to approximate the solution for each subdomain.
These approximations are then incorporated into the primitive equations. A
condition for the finite element method to work, however, is that ψ is continuous between neighbouring elements.
The fact that only low-order polynomials can be used is reflected in the
comparatively low accuracy, but the amount of necessary calculations is much
smaller than for finite differences or for spectral methods [5, p. 4]. On the
other hand, there are a number of choices for the basis functions, and
depending on which functions are used, the finite element method can give very
accurate results when it is applied to irregular grids. Thus, the use of this
method is not restricted to triangular and rectangular grids only as is the
finite difference method. This is -- currently -- probably more important in
engineering and fluid dynamics, where this method is most widely used. However,
scientist are constantly trying to improve existing and find new mathematical
methods that model atmospheric processes better than the methods in use
nowadays.
4.4) Current Research
To get to the point, most
of today's research in meteorology is devoted to improving current forecasting
models. This involves the use of enhanced observation and measurement
techniques as well as refining the mathematical models. Several ways to improve
forecast quality are already known in theory, but they cannot be implemented
due to a lack of computer power. The fastest computers in civilian use are
already used by the leading weather services, meaning that many weather
services, especially in developing countries, have to resort to much slower
computers. Since the 1960s, when issuing numerical weather forecasts calculated
by computers on a regular basis begun, forecast accuracy has been accompanied
by the development of faster computers, and it seems that this will be the case
for the foreseeable future.
One of the easiest ways to
increase the quality of weather predictions is to increase the orders of the
numerical approximations to partial differential equations. Most schemes used
in current models are of second order, but using third-order schemes would
greatly improve forecast accuracy [29]. In addition, both data collection and data
assimilation are constantly improved. Thereby, the initial conditions entered
into forecasting models represent the actual state of the atmosphere more
accurately, which leads to better forecasts [29].
More detailed and more
accurate mathematical methods as well as increased computer power will allow
meteorologists to increase the resolution of their grids. A finer resolution
will in turn allow them to take local weather phenomena such as thunderstorms
as well as the effects caused by topographic features such as mountains and
lakes into account. Ultimately, this will result in very detailed forecasts --
so meteorologists hope -- for very small specific regions. Most models include
as many topographical features as possible, but according to the DWD, there is
a new grid model using horizontal planes cutting through mountains, permitting
a more accurate representation of the equilibrium of the atmospheric forces in
the proximity of mountains. Admittedly, increasing the grid resolution involves
the risk that errors in the initial data are multiplied when more grid points
are used [41], so mathematical models will have to take this into account.
Apart from increasing the
grid resolution, meteorologists also work towards increasing the time span for
which forecasts can be made. The two weeks limit conjectured by Lorenz still
stands; currently the achievable limit is considered to be about ten days. In
February 2010, the ECMWF successfully produced accurate ten-day forecasts for
the first time ever. The accuracy of a medium-range forecast is measured in
terms of the anomaly correlation coefficient (ACC), which has to be above 60%
in order for a forecast to be considered accurate. The February forecasts of
the ECMWF were consistently above this limit [32].
Of course, fundamental
research both in mathematics and in physics concerning atmospheric processes
and the underlying mathematical and physical laws will continue to be crucial
for the development of better forecasting models. A team of international
researchers, led by Shaun Lovejoy of McGill University in Montreal, follows a
different path than most scientist studying atmospheric processes.
Interestingly enough, their research project is based on a theory by Lewis Fry
Richardson. Apart from founding numerical weather forecasting, Richardson
devoted a considerable amount of time to studying the atmosphere, in particular
eddies and whirls. He noticed that atmospheric phenomena, for example clouds,
seem to be cascade-like processes, with large-scale structures containing many
ever-smaller copies of themselves, like Russian dolls sitting inside each
other. In modern mathematics, this kind of phenomenon is called a fractal and
its behaviour can be described using power laws (meaning that one quantity
changes as another quantity is raised to some power). Richardson did not have
the mathematical means to prove his assumptions, and mathematicians have only
recently begun to investigate if the atmosphere can be described by a set of
power laws. In a report published in 2009, Lovejoy's team provides evidence
that rainfall is indeed a collection of fractals. The team's ultimate goal is
to implement fractals and power laws in forecasting models in order to model
small-scale processes and hence improve forecasting accuracy [25].
5) Conclusion
Weather forecasting has
come a very long way since the Babylonians and the Greeks started observing the
skies, and it was the pioneering work of Vilhelm Bjerknes and Lewis Fry
Richardson at the beginning of the 20th century that kicked off the development
of modern weather forecasting. But without the invention and subsequent
improvement of computers, numerical weather prediction would still be in its
infancy. Understanding chaos and developing new and better weather observation
methods also contributed to improving forecast accuracy. A six-day forecast
nowadays is now as accurate as a one-day forecast in 1968 [29]. Current one-day
forecasts are accurate in 9 out of 10 cases, and three-day forecasts still have
a hit rate of 70%. Current research suggests that these percentages will
continue to increase in future. Apart from normal weather forecasts, weather
services also issue specialised forecasts for a variety of domains, such as
agriculture, aviation and shipping, which help save lives and money. Still, meteorologists
at the ECMWF estimate that the global economic loss due to inaccurate weather
forecasts amounts to up to a billion Euros per year [26], so meteorologists
hope that improved forecast quality will reduce this number.
The two different types of
forecasting models, one of them based on finite differences, the other one
based on the spectral method, are currently competing as to which one of them
yields more accurate forecasts for a given computational cost. But at the end
of the day, each model has its strengths and weaknesses; so using both models
side by side will probably give the best results.
In the future, weather forecasts will be even more accurate and more detailed
than forecasts nowadays. And who knows, maybe one day mathematicians will find
a way to overcome the two weeks forecasting limit, so that long-range forecasts
can be produced.
Article by: Stefanie Eminger (University of St
Andrews)
May 2011
MacTutor History of
Mathematics
[http://www-history.mcs.st-andrews.ac.uk/HistTopics/Weather_forecasts.html]