Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Актуальність теми
- 2. Мета і задачі дослідження та заплановані результати
- 3. Огляд досліджень та розробок
- 3.1 Огляд міжнародних джерел
- 3.2 Огляд національних джерел
- 3.3 Огляд локальних джерел
- 4. Реалізація методів трасування променя на різній архітектурі
- Висновки
- Перелік посилань
Вступ
Тривимірна графіка – область знань, яка отримала безмежні можливості завдяки безперервному розвитку інформаційних технологій, удосконаленню апаратного забезпечення електронних обчислювальних систем, зростанню продуктивності комп'ютерної техніки.
Пошук рішення проблеми синтезу фотореалістичних зображень привів до розробки різних алгоритмів розрахунку освітлення сцени.
Серед існуючих методів фотореалістичної візуалізації, трасування променів є "ядром" більшості моделей візуалізації, які генерують такі зображення. Трасування променів – це метод генерування реалістичних зображень, в якому промені світла проходять від спостерігача до точок дотику з об'єктами сцени зображення.
1. Актуальність теми
Актуальним завданням комп'ютерної графіки є отримання реалістичних зображень, які активно користуються попитом у промисловості, ігрової індустрії і кіно. Фотореалістичне зображення характеризується такими ефектами, як м'які тіні, півтіні, каустика, динамічне розмиття, глибина різкості, нечіткі відображення, блиск, напівпрозорість. Серед існуючих методів фотореалістичної візуалізації методи трасування променів є найбільш точними, оскільки засновані на фізичній моделі розповсюдженні світла.
Існує багатий спектр різноманітних методів трасування променів, таким чином, з'являється необхідність у вибіру найбільш ефективних точних методів трасування променів, які будуть в середньому коректно працювати для широкого ряду візуалізіруемих статичних і динамічних сцен.
2. Мета і задачі дослідження та заплановані результати
Метою дослідження є аналіз існуючих методів фотореалістичної візуалізації, підвищення їх ефективності, а також відображення методів на архітектурy паралельних комп'ютерних систем.
Основні завдання дослідження:
- Аналіз існуючих методів трасування променів, тим самим відібрати з них ті методи, які дають можливість отримати високоякісне реалістичне зображення.
- Розробка модифікованих методів трасування променя.
- Відображення методів на архітектурі паралельних комп'ютерних систем, зокрема, використовуючи засоби GPGPU – CUDA.
Об'єкт дослідження: фотореалістичний рендеринг.
Предмет дослідження: модифікація точних unbiased методів, з метою зменшення часу рендеринга на один кадр, і відображення їх на архітектурі GPU.
3. Огляд досліджень та розробок
Концепція будь-якого алгоритму трасування променів полягає в тому, щоб ефективним способом знайти точки перетину променя зі сценою, що складається з геометричних примітивів, таких як полігони, сфери, конуси і т.д. По суті, будь-який об'єкт сцени може бути використаний як примітив, якщо можливо обчислити точку перетину променя з цим об'єктом.

Рисунок 1 – Процес рендеринга методом трассування променів
(анімація: 5 кадрів, 5 циклів повторювання, 28.1 кілобайт)
3.1 Огляд міжнародних джерел
Вперше метод трасування променів був запропонований Уіттедом (Whitted). Основа цього методу полягає в випущенні променів від спостерігача, і наступного пошуку перетину з об'єктами сцени. Кожний видимий перетин променя з поверхнею генерує безліч променів в переломленому, відбитому та у напрямку до джерела світла траєкторіях. Цей процес повторюється до тих пір, поки жоден із нових згенерованих променів не перетнеться з яким-небудь об'єктом.
Модель глобального освітлення, описаної в роботі "An Improved Illumination Model for Shaded Display" (Turner Whitted, Bell Laboratories, Holmdel, New Jersey, 1980) [1] враховує закон Ламберта, згідно з яким яскравість, розсіює світло дифузної поверхні, однакової у всіх напрямках. Цей закон застосовується для примітивних поверхонь, для більш складних моделей поверхні використовується модель Фонга. Остання модель передбачає, що кожне джерело світла розташоване в точці нескінченно віддаленої від об'єктів на сцені. Дана модель не підходить для об'єктів, "поведінка" яких схоже на джерело світла або для світла який відбивається від об'єкта до об'єкта. Тут модель Блінна-Фонга для дзеркального відображення навколишнього середовища об'єкта на сам об'єкт. Модель глобального освітлення в роботі Уіттеда передбачає імітацію тіней. Точка на поверхні лежить в тіні, якщо вона є видимою для спостерігача, але невидима для джерела світла. Розглянуто проходження променя світла крізь прозорі об'єкти.
Переваги методу: правильно розраховані відображення, первинне освітлення і тіні. Основа методу на законах геометричної оптики, таких як закон прямолінійного поширення світла, принцип оборотності, закон заломлення, закон відображення. Недолік методу полягає в тому, що візуалізоване зображення недостатньо фотореалістичне.
Метод розподіленого трасування променів [2]. Передумовами нововведення було недолік ефектів алгоритмів трасування променів, таких як розмиття зображення, глибина різкості зображуваного простору, м'які півтіні, нечіткі відображення. З огляду на те, що напрямки променів чітко визначені, це обмежує можливості методу трасування променів. Наслідком цього є різкі тіні, відблиски і заломлення. Для чіткого розуміння ідеї розподіленого трасування променів необхідно зрозуміти, що таке семплювання. Семпл – це значення функції в деякій точці, а семплювання – це спосіб обчислення деякої функції на безлічі з використанням семплів. За допомогою належного згладжування (aliasing), промені можуть семплювати розмиття, лінзи камери. Ідея методу полягає в розподілі напряму променів згідно аналітичної функції, яка семплюеться по цих напрямках, здатна реалізувати нечіткі явища (розмиття, глибина різкості і т.д.). Завдяки семплюванню в методі розподіленого трасування променів можливі такі ефекти:
- семплювання відбитого променя в залежності від дзеркальної розподіленної функції дає ефект блиску (blurred reflection);
- семплювання відправленого променя забезпечує напівпрозорість (blurred transeperency);
- семплювання тілесного кута джерела світла виробляє півтіні;
- семплювання простору об'єктива камери дає ефект глибини різкості;
- семплювання в часі дає ефект розмиття в русі.
Переваги: Метод розподіленого трасування променів вдало адаптований для алгоритмів порядкового сканування. Він включає в себе розрахунки глибини різкості для видимих поверхонь, усуваючи недоліки попередніх методів. За допомогою даного методу можливі розмиті ефекти, використовуючи розподіл променів в часі. Недоліки: Відмінності в тінях, півтінь і повної видимості вцілому, аргументовано розрахунками глибини різкості. Зміни в глибині різкості і в видимості – динамічно розмиті. Обчислення тіней і півтіней динамічно розмиті. Всі ці явища взаємопов'язані, і новий підхід вирішує їх разом семплюванням багатовимірного простору, якого вони визначають. Ключем до цього є згладжування семплу.
У роботі [3] розглянуто метод прямого і зворотного трасування променя. Ідея полягає в генеруванні променів, наступних від джерела світла, і вдаряються об об'єкти сцени, до камери. Проблема полягає в тому, що більшість променів так і не досягають камери. Ці промені ніяк не впливають на картинку, тому симулювання такого алгоритму безглуздо. Швидкість візуалізації сцени таким методом дуже мала, у зв'язку з цим ніде не використовується. Для вирішення такої проблеми покликаний метод зворотного трасування променів.
Метод зворотного трасування променя. Причиною його виникнення було те, що традиційні алгоритми трасування променів, з їх моделлю освітлення, не враховують дифузне відбиття від непрямого освітлення. Алгоритм розглянутого методу: генерування первинного променя з віртуального ока (камери), пошук перетину променя з поверхнею сцени, генерування тіньового, відбитого, переломленого променів з точки перетину, обчислення характеристик глобального освітлення в залежності від фізичних властивостей об'єктів.
У роботі [4] викладено метод радіосіті (radiosity) і алгоритм полукуба для розрахунку форм-факторів, який призначається для обчислення дифузних відбиттів від об'єкта до об'єкта в складному середовищі, що містить приховані поверхні і тіні. Для виконання розрахунків потрібно специфікація взаємного розташування об'єктів сцени, і при цьому положення спостерігача не враховується. Метод излучательности описує баланс рівноваги енергії всередині замкнутого простору. Заздалегідь встановлено, що всі процеси відображення ідеально дифузні. Однак, минула історія або напрям променя втрачається після відбиття про поверхню. Світло, що виходить від поверхні (випромінювальні) складається з самоіспускающего світла і відбитого або проходить суміжного світла. На першому кроці цього методу всі поверхні сцени розбиваються на патчі. Патч – елементарна одиниця поверхні. Дискретизація поверхні на патчі дозволяє замінити інтеграл у рівнянні освітленості на кінцеву суму інтегралів спеціального виду. Кожен такий інтеграл, званий форм-фактором, задає взаємний вплив двох окремих патчів. Знаючи значення кожного форм-фактора, процес синтезу зображень зводиться до розв'язання системи лінійних алгебраїчних рівнянь. Основні труднощі в алгоритмі – розрахунок форм-факторів. Алгоритм полукуба для розрахунку форм-факторів, відповідно до такого підходу форм-фактор може бути розрахований геометричним способом за аналогією Нуссельта.
Переваги методу полягають у правильному відображенні дифузного освітлення. Недоліком можна вважати те що, метод підходить тільки для тих сцен, в яких виконано вимогу замкнутості системи. Наприклад, для сцени з матеріалами заданими за моделлю Фонга, такий алгоритм не підійде. Другим недоліком є труднощі обчислення форм-факторів.
Автор статті "The rendering equation" Джеймс Каджия формалізував задачу візаулізаціі [5]. Рівняння рендеринга – інтегральне рівняння, узагальнююче безліч відомих алгоритмів візуалізації. Алгоритм візуалізації розширює спектр оптичних явищ, які можуть ефективно моделюватися. Рівняння свідчить, що передається інтенсивність світла від однієї точки поверхні до іншої – це просто сума випромінюваного світла і загальної інтенсивності світла, яка відкидається по осі х від усіх інших точок поверхонь. На відміну від рівняння радіосіті, тут не робиться ніяких припущень щодо характеристик відбиття від поверхонь.
Метод Монте-Карло. При створенні фізично коректної моделі розповсюдження світла, за допомогою якої можливо точне обчислення освітленості, моделювання складних оптичних систем, використовується трасування променів на основі методу Монте-Карло. Для фізично коректного моделювання освітленості і побудови фотореалістичних зображень в роботі використовуються методи прямого і зворотного трасування променів.
Завдання глобального освітлення лежить в основі всіх підходів до фотореалістичної візуалізації. Тут враховується пряме і вторинне освітлення. Всі методи розрахунку глобального освітлення є наближеними рішеннями інтегрального рівняння рендеринга. Для вирішення цього рівняння застосовуються наближені методи чисельного рішення. Методика на основі методів Монте-Карло і трасування променів чисельно вирішує рівняння рендеринга, дозволяючи з високою точністю розраховувати освітлення сцен і будувати зображення високореалістічної якості.
Ідея методу Монте-Карло прямого трасування променів полягає в статистичному відтворенні механізму поширення світла шляхом моделювання всіляких траєкторій променів. Траєкторії світлових частинок (фотонів) простежуються на всіх етапах існування, від моменту їх генерації джерелами світла до поглинання або виходу з сцени. Напрямок, в якому випускається фотон, і стартова позиція на джерелі світла визначаються стохастично згідно фотометричному розподілу енергії джерела та його геометричній формі. Траєкторія фотона трасується до перетину з поверхнею. При взаємодії фотона з поверхнею, він може бути поглинений, дифузно відображено (заломлюючись) з рівномірною щільністю розподілу по півсфері, відображений (заломлюючись) в дзеркальному напрямку, або відображений (заломлюючись) згідно заданої щільності розподілу. При виборі подальшої поведінки фотона згідно властивостям поверхні (наприклад, дифузного або дзеркального відображення) використовується принцип рулетки. Метод не залежить від положення ока спостерігача і не здійснює безпосереднього виведення зображення на екран, а лише надає дані про освітленість для алгоритмів зафарбовування зображень, тобто будує так звану карту освітленості, яка є рішенням задачі глобальної освітленості. Метод природним чином підтримує всі типи поверхонь, включаючи довільні поєднання дифузних і дзеркальних властивостей, як при відбитті світла від поверхонь, так і при його пропущенні через прозорі і напівпрозорі матеріали. Для завдання нетривіальних оптичних властивостей поверхні може використовуватися двоспрямованаа функція, що описує щільність розподілу віддзеркалень і заломлень. Повна інформація про прийоми методів Монте-Карло викладена в роботі [6].
Після того як глобальна освітленість сцени розрахована методом Монте-Карло, її фотореалістичне зображення можна побудувати за допомогою детермінистичного алгоритму зворотного трасування променів. Для незатінених області розраховується сумарний коефіцієнт поглинання світла при взаємодії з зустрічними на його шляху до джерела поверхнями і середовищами. Отримане трасуванням первинних променів, зображення доповнюється "дзеркальними" відображеннями, а також видом через прозорі поверхні. Для цього алгоритм трасування застосовується до кожного віддзеркалення або заломлення променю.
Стратегія вибірки за значимістю для трасування променів методом Монте-Карло, в якій груба оцінка інтенсивності сяйва побудована на основі фотонних карт і локальної моделі відображень, дозволяє конструювати більш ефективні імовірнісні функції щільності. Ці функції можуть використовуватися у схемі вибірки за значимістю. Алгоритм, представлений в [7] дає на виході результати без припущень, підтримує моделі відображень і ефективний у сценах з неоднорідним непрямим освітленням. Переваги методу Монте-Карло: процедурна геометрія сцен, легке відтворення дзеркальних відображень, низьке споживання пам'яті, точність контролюється на рівні пікселя, легко реалізується.
Єдиний недолік – це поява шуму на зображенні після виконаної візуалізації. Застосування: сфера проектування систем освітлення будівель та інших об'єктів міського будівництва. Графічна система дозволяє при розробці архітектурних і світлотехнічних рішень побачити, як виглядатиме інтер'єр, будівля або комплекс архітектурних (інженерних, скульптурних) споруд в існуючому ландшафті при різних умовах природного або штучного освітлення до початку їх реального втілення.
Двоспрямоване трасування шляху – це вдосконалений метод Монте-Карло [8]. Тестові результати показують порівняно кращу якість зображення для сцен замкнутого типу, де важливу роль відіграє непряме освітлення. Основна ідея методу полягає в одночасному генеруванні променів з обраного джерела світла і віртуального ока. Створюються відрізки шляху, починаючи з віртуального ока і інші відрізки шляху, які беруть свій початок з джерела світла. Довжини кожного з відрізків шляху визначається виходячи з довжини максимального шляху, або за допомогою методу російської рулетки, який випадково зупинить шлях після певного критерію. За наявності двох скомбінованих шляхів, які утворюють ребра між кінцями кожного відрізка шляху, створюється один шлях від віртуального ока до джерела світла. Для перевірки правильності складеного шляху, точки перетину шляхів променя з об'єктами сцена йде від віртуального ока і з джерела світла з'єднуються між собою тіньовими променями. Використовуючи такий підхід, різні світлові комбінації беруться до уваги, не тільки з первинних джерел, а й з вторинних, третинних, і т.д. джерел світла.
Metropolis Light Transport, алгоритм без припущень, і неупереджений алгоритм Монте-Карло, призначений для вирішення проблем глобального освітлення, таких як: сильне непряме освітлення, каустика, малі геометричні отвори. Ключовою ідеєю методу є повторне використання шляхів передачі світла з метою отримань так званого внеску в підсумкове зображення.
Алгоритм складається з двох етапів. На першому етапі, двоспрмований трасувальник променів використовується для генерування вихідної послідовності шляхів передачі світла. На другому етапі, кожен початковий шлях мутує, і в свою чергу, кожна мутація або приймається, або відхиляється залежно від ретельної відібраної ймовірності, для того щоб шляхи, котрі піддаються Семплювання, давали кращий ефект. У даному контексті, мутація являє собою переміщення, видалення або додавання вершини. На завершальному етапі, відбувається запис результуючих шляхів на площину зображення.
Особливості прийняття ймовірностей, етапу ініціалізації, вибору підходящої мутації, огляд стратегій мутації [9, 10]. Переваги: Використання малого обсягу пам'яті, простір шляхів досліджується локально за допомогою бажаних мутирование, які вносять невеликі зміни в поточний шлях. Найбільш підходить для сцен з яскравим розсіяним освітленням. Недоліки: даний алгоритм не можна вважати універсальним засобом вирішення всіх проблем глобального освітлення. Застосування: приклад розширення методу MLT [11], де розглядається підхід до реалізації таких об'ємних ефектів як: туман, дим, хмари (participating media). Ці ефекти узагальнюються в категорію анізотропного розсіювання в неоднорідному середовищі. Розширення методу грунтується на внесенні змін у стратегію мутації.
Метод фотонних карт – це універсальний алгоритм, здатний моделювати глобальне освітлення включаючи ефект каустики, дифузні межотраженія. Цей метод забезпечує таку ж гнучкість, як і загальні методи трасування променів на основі методу Монте-Карло, при цьому використовується тільки частка часу обчислення. Постановка завдання методу фотонних карт зводиться до обчислення інтеграла освітленості. Самі фотони представляють собою частки, що транспортують певну порцію світлової енергії. Далі, при зіткненні фотона з деякою поверхнею, фотон може відбитися дифузно/дзеркально, пройти крізь або поглинутися.
Алгоритм методу фотонних карт починається з генерування з джерела світла фотонів. Кількість фотонів залежить від розподілу світлової енергії даного джерела світла. Після завершення трасування фотонів складається фотонна карта, що представляє собою структуру просторового розбиття. Це необхідно для вибірки певної кількості фотонів в довільній точці простору. Для зберігання фотонів використовуються kd-дерева (бінарні дерева, що розбивають простір площинами, паралельні осям координат). Після побудови фотонної карти починається етап збору освітленості. Тут використовується або розподілена трасування променів, або константний радіус збору.
Алгоритм глобального освітлення побудований на фотонних картах, що являє собою двопрохідний метод. Перший прохід будує фотонні карти, випускаючи фотони з джерела світла в сцену і зберігаючи їх в фотонной карті, коли вони стикаються з недзеркальними об'єктами. Другий прохід, етап візуалізації, використовує статистичну техніку на фотонних картах для добування інформації про вхідний поток світлової енергії і відбитому сяйві в будь-якій точці в сцені. Фотонні карти окремо зберігаються від геометричного представлення сцени. Це ключова здатність алгоритму, робить його здатним до моделювання глобального освітлення в складних сценах, які містять мільйони трикутників, об'єктну геометрію, і складно процедурно-визначених об'єктів. Детальніше про це підході викладено в джерелі [12].
Як і раніше імітація глобального освітлення залишається складним завданням. Найбільш кращим підходом є комбінування методів излучательности і трасування променів. Переваги: метод фотонних карт підтримує недіффузние об'єкти і ефекти каустики. У порівнянні з методами Монте-Карло і двоспрямованого трасування променів, метод фотонних карт відрізняється його ефективністю. Для більшості сцен метод фотонних карт значно швидше, і результат виглядає краще, через те, що помилка в цьому методі має низьку частоту, ніж в методах Монте-Карло. Іншою перевагою цього методу є відсутність на нього патенту, хто завгодно може скористатися методом фотонних карт для свого рендера. Недолік: для зберігання інформації про фотонах доводиться платити пам'яттю [13]. Двоспрямована оціночна функція для сяйва, вагова функція, особливості дзеркальних поверхонь викладені в джерелі [14].
Метод об'ємного рендеринга для сцен, що містять об'ємні геометричні дані. Основою даного методу є сортування всіх об'єктів вздовж променя з перетинаннями і по відстанях. І лише після цієї процедури виконуються інші розрахунки. Результати перетинань обробляються шейдером, який оцінює рівняння інтенсивності, необхідне для освітлення моделі з метою визначення остаточного значення пікселя.
Раніше для об'ємного рендеринга використовувалася тільки локальна модель освітлення. У джерелі [15] представлена глобальна модель освітлення і ефективна техніка рендеринга для об'ємних даних. Це обгрунтовується тим, що глобальні ефекти можуть бути корисними для науково-дослідних програм. А також більшість вчених прийшли до висновку про придатний перегляд даних з проекціями максимальних значень. Іншою причиною є обчислювальна ефективність техніки рендеринга. Складні об'єкти зазвичай створюються за допомогою операцій конструктивної стереометрії (CSG). У розглянутому методі складні поверхні легше візуалізуються. По-перше, всі CSG-операції обчислюються заздалегідь, і в результаті один об'ємний об'єкт, замість CSG-дерева геометричних примітивів. А також, необхідна тільки одна процедура перетину з поверхнею для об'ємних об'єктів, у той час як у класичній трасуванні променів така процедура виконується для кожного геометричного примітиву. По-друге, карти текстур можуть бути заздалегідь обчислені для кожного об'ємного об'єкта, таким чином, уникаючи "трудовитрат" на відображення текстур під час трасування променів. Геометрична сцена моделюється воксельними об'єктами і потім візуалізується алгоритмами об'ємного рендеринга.
Методи рендеринга зазвичай складаються із двох частин: моделі освітлення і техніки оцінки цієї моделі для генерування зображення. На відміну від класичного трасування променів, де рівняння глобального освітлення завжди оцінюється в точці поверхні вздовж променя, об'ємне трасування променів оцінює це рівняння тільки на сегменті променя. Застосування методу об'ємного трасування променів використовується в комп'ютерній томографії для отримання та аналізу медичних даних.
3.2 Огляд національних джерел
У Харківській академії міського господарства Ю. О. Васильєвою, і Е. Н. Ляшенко виконано аналіз сучасних методів фізично коректного моделювання поширення світла із застосуванням методу Монте-Карло і показана їх ефективність для отримання фотореалістичних зображень при проектуванні систем освітлення [16].
І.М. Єгоровою та М.А. Потеміним (Харківський національний університет радіоелектроніки) наведено аналіз різних алгоритмів розрахунку освітлення сцени. Досліджено найбільш ефективні моделі візуалізації, що дозволяють отримати високоякісні синтезовані зображення при створенні візуальних образів засобами тривимірної графіки [17].
3.3 Огляд локальних джерел
У Донецькому національному технічному університеті (кафедра комп'ютерної інженерії) Р.В. Мальчевою і А.А. Серьоженко розроблена оптимізація та застосування методу трасування променів в 3D-графіці. Коротко описаний алгоритм, структура, можливості, застосування і приклад використання [18].
4. Реалізація методів трасування променя на різній архітектурі
Протягом багатьох років трасування променів в реальному часі вважається головною метою комп'ютерної графіки. Трасування променів в реальному часі демонструвалася окремими малими сценами на базі CPU з принципом обчислень SIMD, а також великими сценами на мультипроцесорі з пам'яттю і кластері. На даний момент вже доступні спеціальні чіпи для прискорення методу трасування променів в реальному часі. При цьому вивчення реалізації методу трасування променів на різній архітектурі є дорогим процесом.
Альтернативним підходом до реалізації методу трасування променів в реальному часі є використання GPU. Графічне апаратне забезпечення еволюціонувало від Graphics Rendering Pipeline (конвеєр, етапи якого проходить відеокарта для побудови фінального зображення) оптимізованого для візуалізації трикутників з картами текстур до GRP з програмованими верховими і фрагментарними етапами.
Конвеєр для GPU складається з таких етапів: програма, вертексна програма, растеризація, фрагментарна програма, дисплей. З тих пір як графічні процесори стали включати повний набір команд і більшу кількість типів даних, його можна віднести до категорії макропроцесора. З метою, перенести всі обчислення на GPU, було запропоновано розглядати архітектуру графічного процесора як потоковий процесор. Потокові обчислення відрізняються від традиційних, тим, що система зчитує необхідні дані для обчислень як потік елементів. Кожен елемент потоку – це запис даних, яка вимагає аналогічних обчислень. Потокова модель ефективна при реалізації, оскільки дозволяє використовувати паралелізм, поліпшити пропускну здатність, приховати латентність пам'яті.
Відображення методу трасування променів на потокову модель (рис. 2) [19]. Спочатку передбачається, що геометрія сцени представляється трикутниками, які зберігаються в прискорюючих структурах даних. Потоковий трасувальник променів розділений на чотири ядра: виробляє потік видимих променів. Кожен видимий промінь – генерування променів з камери, сітки перетинів, перетинань променя і трикутника, затінення. Генератор променів з камери це окремий промінь, відповідний пікселя зображення. Ядро перетинань зчитує потік променів, вироблених генератором променів. Це ядро послідовно спрямовує промені крізь сітку, поки промінь не зіткнеться з вокселем, що містить трикутники. Наступне ядро перетинань відповідає за тестування перетинань променя з усіма трикутниками всередині вокселя. Ядро затінення обчислює колір, генерує вторинні промені або тіньові промені.
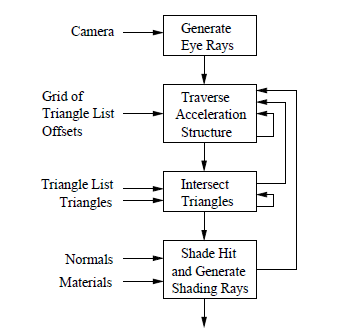
Рисунок 2 – Потокова модель рейтрейсера
Застосування: Швидкий апроксимуючий метод для знаходження точки перетину відбитого або переломленого променя. Розрахунки засновані на величинах відстаней, які зберігаються в текселях карт навколишнього середовища. Апроксимація використовується для локалізації віддзеркалень і заломлення, представлених картами навколишнього середовища, щоб зробити їх незалежними там, де вони трапляються. З іншого боку, розміщуючи віртуальний очей в джерелі світла, цей метод добре спрацює для генерування каустики в реальному часі. Даний метод підходить для сцен, що складається з великих плоских граней. Метод описаний в [20] підходить для GPU архітектури, і застосовується в ігровій індустрії.
У роботі [21] розглядається система Razor, яка підтримує динамічні сцени з високоякісними ефектами (м'які тіні, несфокусірованного розмиття). Ця система виконується на програмованій многоядерній архітектурі і призначається для трасування променів в реальному часі. Система трасування променів Razor, використовує багатопоточність з одним головним потоком і робочими потоками для кожного ядра CPU. Первинні промені організовуються в 2D-блоки, які поміщаються в робочу чергу і відображаються на робочі потоки. Як показано на рис. 3 Razor підтримує видимість за допомогою спеціальної структури kd-дерева, побудованого для кожного кадру, а також використовує так званий "крупно-зернової" паралелізм, за допомогою декомпозиції областей кадрів на клітинки. Крім того, тут використовується паралелізм за допомогою пакетного трасування променів одночасним пусканням безлічі променів, як показано на рис.6. Обчислення матеріальних тіней відокремлені від розрахунків перетинань, оскільки вони дуже відрізняються. На малюнку 3 представлена апаратна організація многоядерной системи.
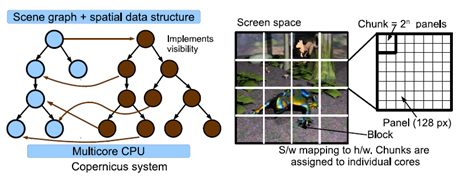
Рисунок 3 – Огляд многоядерной системи
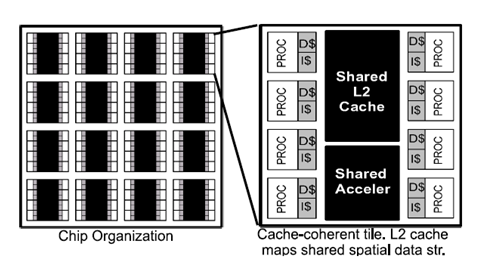
Рисунок 4 – Апаратна організація многоядерной системи
Апаратна архітектура – це крупно-масштабований багатоядерний процесор з приватним кешем другого рівня, багатопоточністю для приховування латентності доступу до пам'яті, і обмежена когерентність кеша. Така організація дає можливість легкого масштабованості на тисячі ядер. Проведені дослідження показали 8-ядерна плитка може бути повністю використана на 100% і підтримувати 10 мільйонів променів/сек. 16 таких плиток можуть вміститися на чіпі (240mm2, технологія 22 nm), і таким чином, без проблем реалізовувати трасування променів в реальному часі.
З появою технологій CUDA NVIDIA і AMD Stream почався перегляд концепцій реалізації трасування променів на GPU. У роботі [22] розглядається реалізація зворотного трасування променів на GPU з підтримкою тіней, відображень, заломлень, прозорості об'єктів і текстурування. Графічна платформа – OpenGL, мова шейдерів – GLSL (забезпечення багатоплатформеності). Особливостями цієї реалізації є: подання всіх об'єктів сцени у вигляді трикутників, використання регулярної сітки з "хмарою близькості" в якості прискорюючою структури, поліпшені алгоритми перетину "промінь-примітив". Необхідні дані для розрахунків передаються текстурами і спеціальними глобальними змінними. Кожен тексель текстури містить зміщення у текстурі вершин, число трикутників та ін. Спеціальні глобальні змінні зберігають дані камери і джерел світла.
У роботі [23] розглядаються варіанти реалізації рекурсивної трасування променів на CUDA. Коли промені кидаються в сцену, їх кінцевою метою є – повернення кольору пікселя і значення кольору пікселя не визначається за значенням кольору сусіднього пікселя. З огляду на те, що найменшим незалежним елементом у трасуванні променів є – піксель, то саме на ньому побудований весь паралелізм обчислень. На CUDA до кожного пікселя прив'язується окремий потік GPU. Цей потік виробляє всі розрахунки освітлення, затінення, перевірку перетинань об'єкт/промінь для всіх об'єктів. По суті, це означає що кожен потік має доступ до повної характеристики сцени.
Так як трасування променів є ресурсовитратним процесом, постійно виникає завдання його прискорення на графічному процесорі. Для вирішення такої проблеми використовують такі прискорюючі структури, як рекурсивні структури просторового розбиття (kd, BVH дерева). Як показав досвід реалізації методів трасування променів на GPU, дана технологія має деякі недоліки. До них відноситься відсутність стека, недостатня кількість регістрів GPU, незмірність швидкості роботи частин алгоритму. У статті [24] ці недоліки компенсуються високим ступенем паралелізму, поділ алгоритму на кілька ядер і їх множинним перемиканням. Враховуючи недоліки технології CUDA в роботі [24], завдання трасування променів декомпозіровано на три підзадачі: пошук в kd-дереві, підрахунок перетинань, затінення. При такому підході вдалося виміряти швидкість частин алгоритму, всі частини програми незалежні один від одного, ядро затінення може бути будь-яким за складністю, що не відіб'ється на продуктивності системи. Деякі алгоритмічні аспекти фотонних карт ускладнюють реалізації на GPU, що відбивається на продуктивності системи. Рішенням стало – угруповання фотонів, в кожній з якої фотони трохи розходяться один від одного. Для наступного етапу, збору освітленості, застосовується вибірка деякого фіксованого радіуса збору та оцінки висвітлення всіх фотонів, які потрапляють в заданий радіус, що економить ресурси GPU. Більш докладно про проблему зберігання фотонів на GPU (CUDA) в ході багатопрохідного алгоритму та її вирішенні в роботі [24, c.6].
Альтернативний підхід до прискорення методу трасування променів на GPU описаний у роботі [25], де пропонується сортування фотонної карти (з метою отримання ефекту каустики) так, щоб зменшити час доступу до найближчих фотонам в області точки зіткнення. Для цього застосовується просторова хеш-функція і бітонічне сортування.
У роботі [26] представлений движок NVIDIA OptiX для трасування променів, спроектований для графічних процесорів NVIDIA. Даний движок був розроблений виходячи з одного важливого спостереження, що більшість алгоритмів трасування променів можуть бути реалізовані за допомогою малого набору програмованих операцій. Ядро движка OptiX являє собою предметно-орієнтований динамічний компілятор, який генерує ядра трасування променів, поєднуючи користувача програми для генерування променів, затінення, перетинів з об'єктами та ін. Цей движок відрізняється високою продуктивністю за рахунок акуратною об'єктної моделі, а також своєю гнучкістю, що дозволяє настроювати і адаптувати движок до певних задачах, підтримкою рекурсії. Дані, які несе і збирає промінь повністю налаштовуються, що спрощує розрахунки для одного променя в одиницю часу. Програмований графічний конвеєр OptiX представлений на малюнку 5 [26, c.3, figure 2].
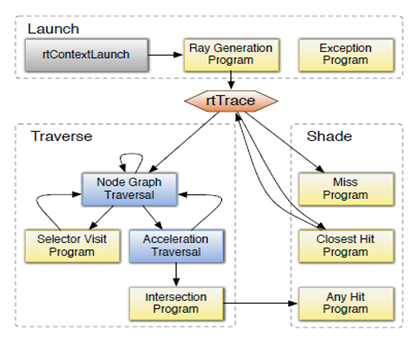
Рисунок 5 – Графічний конвеєр OptiX (граф викликів)
Сцена зберігається і обробляється як граф, в[26, c.3, figure 2] показаний приклад розбиття на граф певної сфери (рис.6).
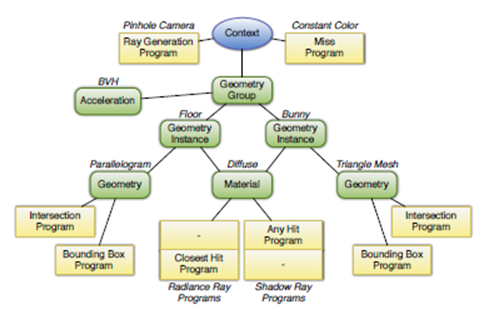
Рисунок 6 – Граф сцени
Управління потоком основної програми OptiX [26, c.6, figure 5] (рис. 7).
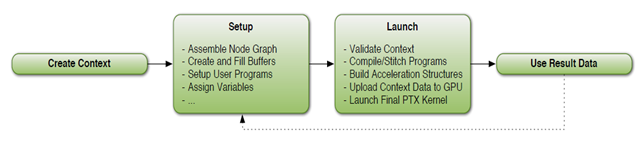
Рисунок 7 – Потік управління програмою
Також OptiX здійснює підтримку графічних API (OpenGL). Функції OptiX: паралелізм всередині GPU, між GPU і CPU, використання kd, BVH дерев та інших обхідних алгоритмів, контроль використання потужностей GPU за допомогою вбудованого модуля з балансування навантаження.
В результаті розгляду безлічі методів трасування променів, для подальшого порівняльного аналізу будуть фігурувати тільки точні методи трасування променів, які на виході дають якісне фотореалістичне зображення. До таких методів належать двоспрямоване трасування шляхів, метод фотонних карт, розподілене трасування променів, MLT.
У роботі [27] пропонується реалізація методів трасування шляхів, двобічного трасування шляхів, а також MLT на GPU (CUDA), з метою показати, що обчислення на GPU набагато краще, ніж на СPU. Експериментальні дані були отримані на апаратурі Intel CoreTMi7 CPU 920 and NVIDIA GeForce GTX 480 (рис. 8).
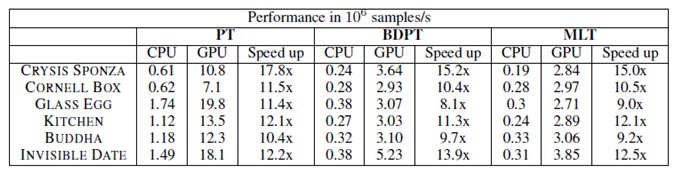
Рисунок 8 – Порівняння продуктивності між CPU та GPU
Висновки
Проаналізувавши методи трасування променів, виділимо групу методів за умовою високої якості і точності вихідного зображення. Зворотне трасування променів балансує між якістю і швидкістю, і так як, цей метод є основою для багатьох інших, то не будемо його відносити до категорії фотореалістичних методів. Розподілене трасування променів володіє широким рядом переваг в плані фотореалістичних ефектів, тому відбираємо його в групу точних методів. Трасування променів на основі методу Монте-Карло і пряме трасування променів лежать в основі багатопрохідних методів. Двосрямоване трасування шляхів, Metropolis Light Transport і метод фотонних карт витримують фільтр по точності та високої якості. Метод об'ємного трасування променів не підходить за обраним критерієм. Таким чином, до методом фотореалістичної візуалізації відносяться методи: розподілене трасування променів, метод фотонних карт, двоспрямоване трасування шляхів і Metropolis Light Transport.
Магістерська робота присвячена актуальній науковій задачі синтезу фотореалістичних зображень. У рамках проведених досліджень виконано:
- Проведено аналіз існуючих методів трасування променя.
- Обрано точні методи фотореалістичної візуалізації.
- Досліджено особливості відображення відібраних методів на архітектуру GPU.
Подальші дослідження спрямовані на наступні аспекти:
- Виконання програмної реалізації методів на CUDA.
- Отримання експериментальних характеристик швидкості і якості.
- Оптимізація методів для зменшення часу візуалізації сцени.
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2013 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.
Перелік посилань
- Whitted, Turner. An improved illumination model for shaded display. Communications of the ACM 6, 23, (June 1980), 343-349.
- Cook, Robert L.: "Distributed Ray Tracing". Computer Graphics 18 (3), pp. 137- 145, 1984.
- Glassner Andrew S. An introduction to ray tracing, Academic Press Inc, San Diego,1989.-327 p.
- Cohen Michael F., Greenberg Donald P., “The hemi-cube, A radiosity solution for complex environment”, Cornell University, Ithaca, N.Y., 1985.
- Kajiya James T., “The rendering equation”, Dallas, August, Vl 20, N.4, 1986.
- H. W. Jensen, J. Arvo, P. Dutre, A. Keller, A. Owen, M. Pharr, and P. Shirley. Monte carlo ray tracing. In ACM SIGGRAPH Course Notes 44, 2003.
- Jensen H. W. Importance driven path tracing using the photon map //Rendering Techniques’ 95. – Springer Vienna, 1995. – С. 326-335.
- Adamsen Mikkel, “Bidirectional path tracing”, July 19, 2009.
- Hakkinen P., "Metropolis Light Transport", 2008.
- VEACH, E., AND GUIBAS, L. J. Metropolis light transport. In SIGGRAPH ’97 (August 1997), pp. 65–76.
- M. Pauly, T. Kollig, and A. Keller, Metropolis Light Transport for Participating Media, Rendering Techniques 2000 (Proc. 11th Eurographics Workshop on Rendering), Springer, 2000, pp. 11–22.
- JENSEN, H, Global Illumination using Photon Maps, Eurographics Workshop on Rendering 1996, 21-30.
- Jensen H. W. et al. A practical guide to global illumination using photon mapping //SIGGRAPH 2002 Course Notes CD-ROM. – 2002.
- Jensen, Henrik Wann: "Importance Driven Path Tracing using the Photon Map". In "Rendering Techniques '95". Eds. P.M. Hanrahan and W. Purgathofer, Springer-Verlag, pp. 326-335, 1995.
- Sobierajski, L. M. Kaufman, A. E. [1994]. Volumetric ray tracing, 1994 Symposium on Volume Visualization, Washington, D.C., pp. 11–18.
- Васильева Ю. О., Ляшенко Е. Н. Вычисление глобальной освещенности методом Монте-Карло //Міжнародний науково-технічний журнал "Світлотехніка та Електроенергетика". – 2010. – №. 3, 4. – С. 16-20.
- Егорова И.Н., Потемин М.А., «Технология синтеза фотореалистичных изображений» // Восточно-европейский журнал передовых технологий. - 2006. - №. 6/2, (24). - С. 66-69.
- Сереженко А.А., Мальчева Р.В. «Оптимизация метода трассировки лучей» 2009. 5я Международная научно-техническая конференция студентов, аспирантов и молодых учёных «Информатика и компьютерные технологии – 2010.»
- Purcell T. J. et al. Ray tracing on programmable graphics hardware //ACM Transactions on Graphics (TOG). – 2002. – Т. 21. – №. 3. – С. 703-712.
- Szirmay Kalos L. et al. Approximate Ray Tracing on the GPU with Distance Impostors //Computer Graphics Forum. – Blackwell Publishing, Inc, 2005. – Т. 24. – №. 3. – С. 695-704.
- Govindaraju V. et al. Toward a multicore architecture for real-time ray-tracing //Proceedings of the 41st annual IEEE/ACM International Symposium on Microarchitecture. – IEEE Computer Society, 2008. – С. 176-187.
- Боголепов Д.К., Турлапов В.Е. –
Интерактивная трассировка лучей на графическом процессоре
. Труды международной научной конференции по Компьютерной Графике и ЗрениюГрафиКон 2009
- 2009. - С. 263–266. - Britton A. D. Full CUDA Implementation Of GPGPU Recursive Ray-Tracing. – 2010.
- Фролов В., Игнатенко А. Интерактивная трассировка лучей на графическом процессоре с применением технологии CUDA //
GraphiCon 2008
. – 2008. – С. 311-312. - Ульянов Д.Я. Об одной реализации метода фотонных карт для визуализации каустик // Труды международной научной конференции
Графикон 2010
. -2010. - С. 328-359. - Parker S. G. et al. Optix: a general purpose ray tracing engine //ACM Transactions on Graphics (TOG). – 2010. – Т. 29. – №. 4. – С. 66.
- van Antwerpen D. Improving SIMD efficiency for parallel Monte Carlo light transport on the GPU //Proceedings of the ACM SIGGRAPH Symposium on High Performance Graphics. – ACM, 2011. – С. 41-50.
