1. Введение
Новая элементная база, используемая при производстве современных оптических систем, таких как осветительные системы жидкокристаллических (ЖК) дисплеев или панелей приборов, основана на сложных физических эффектах. К таким эффектам можно отнести рассеивание света на микронеровностях поверхностей. Распределение неровностей может быть либо стохастическим (шероховатость поверхности), либо специально спроектированным (микро-призмы заданной формы, размера и распределения). Для дизайна оптических систем широко применяются программные системы моделирования, например, система дизайна светопроводящих пластин для подсветки ЖК дисплеев [1]. Эти системы применяют, как правило, метод трассировки лучей света для расчета выходных световых величин и работают с макрообъектами геометрии, что делает невозможным учет «тонких» физических эффектов. С другой стороны, специализированные программы оптического моделирования (например, дифракционное рассеивание на периодических микроструктурах) могут воспроизводить поведение одного элемента и не дают полной информации о поведении оптической системы в целом. Поэтому особо важной является интеграция функциональности, позволяющей учесть рассеяние света на микронеровностях, в программы «стандартного» оптического моделирования. Такая интеграция позволяет производить сквозное моделирование
от первичных источников света до конечного изображения.
Ряд программных комплексов оптического моделирования использует
концепции расширения стандартной функциональности с помощью
специализированных модулей. Например, ASAP [2], LightTools [3] и SPEOS [4]
имеют специальные средства моделирования рассеивания света на микрочастицах. В
случае поверхностного рассеивания эти программы имеют средства построения и
моделирования микроструктурных рассеивающих элементов на поверхностях
светопроводящих пластин. Как правило, такие микрообъекты называются
трехмерными текстурами [5], и позволяют использовать различные типы упаковок
микроэлементов (регулярные или нерегулярные). Однако, решения, используемые
данными программами, не лишены недостатков. Это, как правило, ограниченное
количество микроэлементов (несколько миллионов) и ограниченные возможности
построения формы или распределения микроэлементов. Примеры поверхностного
распределения микроэлементов показаны на рис. 1.

Рис. 1. Пример распределения микроэлементов на поверхностях
светопроводящих пластин.
В данной работе развивается концепция поверхностных оптических элементов
(ОЭ) как средства расширения функциональных возможностей программ
оптического моделирования [6]. С одной стороны, ОЭ – это специализированная
функциональность, позволяющая моделировать сложные физические эффекты. Очевидно, что специализированная функциональность позволяет использовать более
точные и эффективные решения. Например, становится возможным точное описание
геометрической формы рассеивающих микроэлементов, учет изменения состояния
поляризации и использование волновых решений при рассеивании света на
микрочастицах. С другой стороны, ОЭ интегрируются в программные системы
оптического моделирования и естественным образом повышают эффективность и
точность моделирования этих программ. Такая интеграция становится возможной,
если интерфейс между двумя программами жестко зафиксирован. Принимая во
внимание то, что все программы оптического моделирования используют лучевой
подход, интерфейс ОЭ должен быть «лучевым», то есть ОЭ принимает от
программы луч и возвращает луч (или пучок лучей). Внутри себя ОЭ может не
ограничиваться лучевым подходом и использовать надлежащие волновые решения,
что естественно повышает точность моделирования.
Концепция ОЭ была применена на практике в программном комплексе
SPECTER [7], что позволило расширить его элементную базу различными типами
рассеивающих микроэлементов и повысить точность и эффективность
моделирования. Данная статья ограничивается рассмотрением ОЭ одного вида –
поверхности и тела оптической системы.
2. Базовые концепции интерфейса взаимодействия ОЭ с программой
оптического моделирования
Основополагающей концепцией интерфейса взаимодействия ОЭ с программой
оптического моделирования является его абстрактность. ОЭ являются внешними
объектами по отношению к программам оптического моделирования, поэтому его
интерфейс должен быть максимально унифицирован и абстрактен. То есть ОЭ ничего не знает о программе, которая его вызывает, а сама программа может
обращаться к ОЭ посредством фиксированного набора запросов.
На рис. 2 показано, как данный интерфейс реализован для случая
распространения луча в оптической системе. Лучи, излучаемые источниками света,
распространяются внутри светопроводящей пластины. Взаимодействие луча с ОЭ
осуществляется следующим образом:
1. Детектирование пересечения луча с ОЭ. Трассировщик лучей запрашивает
ОЭ, имеется ли пересечение луча с его граничной поверхностью.
2. Преобразование луча ОЭ. Если пересечение найдено, то передается запрос
на преобразование луча (преобразование может включать собственную трассировку
лучей оптическим элементом). Результатом преобразования является луч с новыми
координатами, направлением, цветом, поляризацией и фазой.
3. Продолжение трассировки. Трассировка лучей продолжается с нового
положения и в новом направлении.
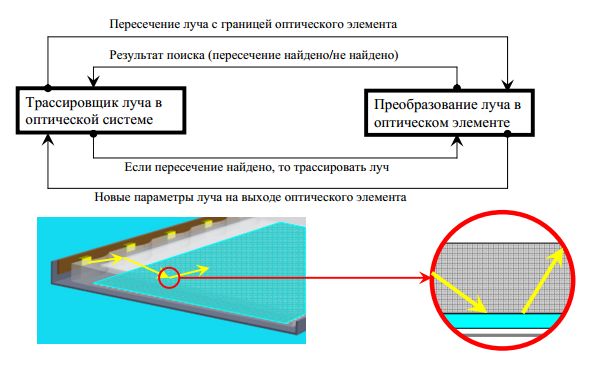
Рис. 2. Преобразование луча ОЭ
Очевидно, что в такой ситуации ОЭ является пассивным объектом и
обрабатывает только внешние запросы со стороны программы оптического
моделирования.
Преимущества абстрактного интерфейса ОЭ и его пассивность проявляются
при интеграции его в среду программы оптического моделирования. Во-первых,
независимо от типа ОЭ (будь это рассеивающая среда, где распространение света
может описываться волновыми законами, или микронеровности на поверхности
оптической системы, где лучевой подход достаточен) внешняя программа
трассировки лучей всегда будет одинаково трактовать ОЭ. Во-вторых, ОЭ с точки
зрения внешней программы являются элементарными объектами и потому не
воздействуют на внутреннюю структуру организации базы данных программы. Все
эти преимущества проявились при интеграции ОЭ в SPECTER.
Важным требованием к разработке интерфейса ОЭ является возможность
работы в распределенных и параллельных вычислениях, то есть в процессе
трассировки лучей ОЭ не может изменять собственные данные, поскольку другой
процесс может их также использовать.
Другое важное требование к интерфейсу ОЭ – это его эффективность.
Технология СОМ не позволяет использовать высокоэффективные решения, потому
весь интерфейс ОЭ был написан на языке C++.
ОЭ предполагает две основные составляющие интерфейса. Это интерфейс
привязки луча к оптической системе и интерфейс трассировки луча.
2.1. Интерфейс создания и привязки ОЭк оптической системе
Процесс создания ОЭ состоит из загрузки ОЭ (его функциональности и
параметров) и уточнения параметров ОЭ, которые имеют отношение к оптической
системе. Необходимо отметить, что, несмотря на свою независимость, ОЭ не могут существовать вне оптической системы. Например, чтобы осуществить
преобразование луча на внешней границе, необходимо знать материал (показатель
преломления) оптической системы, где данный элемент расположен. Поэтому для
нормального функционирования ОЭ кроме собственных параметров должен
импортировать следующие данные оптической системы.
ОЭ импортирует:
1) Внешнюю геометрию ОЭ. Геометрия импортируется в виде треугольной
сетки (массив вершин, массив треугольников как индексов трех вершин и массив
нормалей в вершинах треугольников). Импорт геометрии необходим для
светорассеивающих сред, когда форма рассеивающей среды определена во внешней
геометрии оптической системы
2) Оптические свойства внешних материалов ОЭ. Импорт оптических свойств
необходим, например, в случае, если ОЭ находится в контакте с другим ОЭ.
2.2. Интерфейс трассировки лучей
В качестве базового подхода для всех световых расчетов используется метод
трассировки лучей света. На вход оптического элемента поступает луч, а на выходе
мы имеем луч (или пучок лучей) и описание событий, произошедших с лучом
внутри ОЭ. Количество лучей на выходе зависит от метода, используемого при
преобразовании лучей. В случае «русской рулетки», используемой в трассировке
лучей методом Монте-Карло [8, 9], луч не разделяется на части и распространяется
до тех пор пока не поглотится или не покинет ОЭ.
Для трассировки лучей через ОЭ используются два основных метода,
показанных на рис. 2:
1. Нахождение пересечения луча с границей ОЭ. Независимо от того
присоединен ли ОЭ к объектам оптической системы или он является независимым объектом, процедура нахождения пересечения луча с границей ОЭ является
обязательной. Эта процедура уточняет положение ОЭ в системе и позволяет решить,
реально ли луч пересекается с ОЭ или нет. Кроме того, луч переводится в локальную
систему координат ОЭ.
2. Преобразование луча на ОЭ (или трассировка луча через ОЭ). Вызов метода
преобразования луча возможен только после успешного нахождения пересечения с
его границей. На вход метода подается луч, найденный на предыдущем шаге. Метод
осуществляет преобразование этого луча. Для преобразования луча допускается
использование любых подходов (от лучевой трассировки до волновых решений).
Единственное условие – на выходе должен быть луч (или пучок лучей).
Оба метода имеют два входных/выходных параметра. Первый – это луч, а
второй – это контекст луча. Луч несет основную информацию, как-то координаты,
направление, цвет, состояние поляризации, фазу. Контекст луча несет
дополнительную информацию о прохождении луча сквозь ОЭ. Эта дополнительная
информация является:
• «открытой», ее может использовать внешний трассировщик лучей (история
прохождения луча сквозь ОЭ, датчик случайных чисел и т.п.),
• «закрытой», ее использует только ОЭ (эта информация, как правило,
необходима для передачи данных между методом нахождения пересечения луча с
границей ОЭ и методом преобразования луча).
3. Процедурное описание ОЭ
ОЭ представляет собой процедуру, управляемую набором внешних параметров.
Процедура является полным описанием ОЭ и содержит всю информацию,
необходимую для создания и функционирования ОЭ. Процедура имеет текстовое представление и может быть сформирована любым текстовым редактором. Она
состоит из двух основных частей:
1) Описание внешних параметров. Внешние параметры ОЭ – это такие
параметры, которые могут быть определены извне процедуры. Обычно внешние
параметры процедуры определяются в специальном файле параметров, который
умеет читать ОЭ. Однако эти параметры могут быть заданы непосредственно,
используя пользовательский интерфейс работыс параметрами.
2) Собственно тело процедуры. Тело процедуры это внутренняя часть ОЭ. Ее
формат не определен и зависит от ОЭ. Процедура поддерживает выполнение
основных арифметических и логических операций, стандартных функций, а также
многострочных конструкций с использованием операций условного перехода и
циклов. Процедура позволяет использовать все внешние параметры как константные
объекты (изменение внешних параметров не позволяется внутри тела процедуры).
Однако допускается определение собственных (внутренних) переменных, массивов
и функций, что значительно упрощает описание ОЭ.
Пример процедуры, описывающей распределение микрообъектов (полусфер)
на плоскости, представлен на рис. 3. Пример показывает, как ОЭ задаются в
программном комплексе SPECTER.
Видно, что ОЭ управляется тремя параметрами, чьи значения определены в
файле параметров. Тело процедуры состоит из четырех основных секций:
1. Привязка ОЭ к внешней оптической системе. Здесь производится импорт
оптических свойств и граничной геометрии ОЭ.
2. Область определения ОЭ и основные параметры распределения (дистанция
между полусферами).
3. Распределение микроэлементов (в данном примере полусферы
распределены по регулярной решетке с постоянным шагом).
4. Форма микроэлемента (в данном примере – полусфера).

Рис. 3. Пример процедурыраспределения микро-полусфер на плоскости
Процедурное описание ОЭ, управляемого набором внешних параметров,
позволяет организовать пользовательский интерфейс ОЭ в системе оптического
моделирования. Примером такой организации может служить программный
комплекс SPECTER, который позволяет пользователю изменять параметры ОЭ в
стандартном пользовательском интерфейсе.
4. Интеграция ОЭс поверхностным рассеиванием в систему SPECTER
ОЭ с поверхностным рассеиванием были интегрированы в программный
комплекс оптического моделирования – SPECTER [7]. В основе SPECTER лежат
алгоритмыпрямой трассировки лучей методом Монте-Карло [9].
ОЭ с поверхностным рассеиванием – это набор (микро) геометрических
элементов, нанесенных на поверхность оптической системы. Как правило,
микроэлементы используются в светопроводящих пластинах (для вывода света из
пластины) и как рассеивающие элементы пленок (для создания необходимой
гониометрической диаграммы излучения).
Светорассеивающие микроструктуры имеют два основных представления:
1) Статистическое представление (шероховатая поверхность).
Микроструктуры данного типа определяют локальный рельеф поверхности и могут
быть представлены явно (распределение высот рельефа на координатной сетке) и
неявно (распределение углов вариаций нормали рельефа). В соответствии с
векторами ориентации и нормали к поверхности микрорельеф, определенный в
локальной зоне, распределяется по всей поверхности, к которой присоединен
данный ОЭ. Пример такой микроструктуры показан на рис. 4.
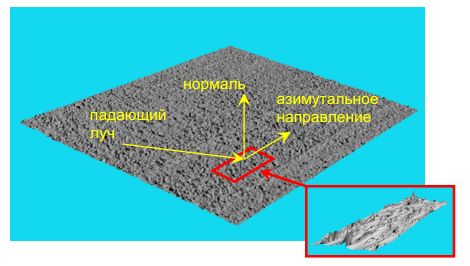
Рис. 4. Пример микроструктуры типа шероховатая поверхность
Как правило, при реальном моделировании используется явное распределение
высот микрорельефа поверхности, измеряемое 3D сканерами. При незначительном
снижении эффективности моделирования (по сравнению с неявным) явное задание
микрорельефа обеспечивает высокую точность, поскольку учитываются эффекты
переотражения света между гранями микрорельефа. Эти эффекты особенно важны
при моделировании скользящего падения света. Необходимо отметить, что данный
подход к моделированию нерегулярных микроструктур отсутствует в большинстве
программ оптического моделирования.
2) Регулярные микроструктуры. Микроструктуры данного типа полностью
определяют рельеф поверхности и представляют собой ряд микрогеометрических
элементов, распределенных по некоторому закону на поверхности оптической
системы. Форма микрогеометрического элемента представляет собой логическую
операцию, объединяющую как элементарные геометрические примитивы (плоскость
и примитивы до четвертого порядка), так и сложные геометрические примитивы
(пирамиды, треугольные сетки) (см. рис. 5).

Рис. 5. Примеры построения форм микроэлемента
Используя данный механизм, можно построить практически любую форму
микроэлемента и параметризовать ее с помощью многомерных функций или таблиц.
Выделяются шесть типов регулярных микроструктур, как показано на рис. 6.
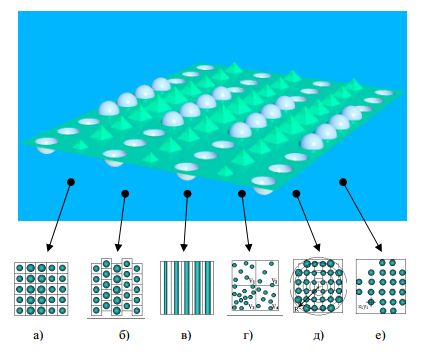
Рис. 6. Типы рассеивающих микроструктур
а) Микроэлементы распределены в узлах прямоугольной решетки.
Количество элементов практически неограниченно и может достигать 1018
. Однако
изменение формы микроэлементов допускается только вдоль одной из
координатных осей ОЭ.
б) Распределение микроэлементов аналогично предыдущему, однако четные
ряды микроэлементов смещены на половину периода.
в) Одномерное распределение микроэлементов (позволяет задавать
призматические слои сложной формы).
г) Случайное распределение микроэлементов заданной плотности. Форма,
размер и ориентация микроэлемента не изменяется. Положение элементов есть случайная функция от плотности распределения, а их количество может достигать
30 млн.
д) Микроэлементы распределены в узлах прямоугольной решетки.
Количество элементов ограничено примерно 30 млн. Параметры элементов
(размер, ориентация и положение) определяются произвольной двумерной функцией
или процедурно.
е) Микроэлементы распределены произвольным образом. Количество
элементов – до 30 млн. Параметры микроэлементов (размер, ориентация и
положение) индивидуальны для каждого элемента (процедурно или в таблице).
Кроме того, этот тип микрогеометрии допускает наличие принципиально различных
форм элементов (полусфера и цилиндр, например) и их ориентации по отношению к
базовой плоскости (вверх или вниз). Этот способ задания микрогеометрии является
наиболее мощным и используется для построения сложных микроструктур.
Единственный его недостаток – незначительное снижение эффективности (скорости)
моделирования.
Очевидно, что предлагаемое решение обеспечивает наивысшую гибкость и
точность построения моделей реальных светорассеивающих элементов. Допускается
построение практически любой формы микроэлемента и любого распределения этих
элементов. Никаких упрощений (например, замена формы элемента на
распределения нормалей или распределения микроэлементов на текстуру) при этом
не делается. То есть достигается максимальная точность моделирования. Поскольку
описание ОЭ является процедурным и управляется внешними параметрами, то
упрощается проектирование и оптимизация оптических систем с этими элементами.
Так как количество микроэлементов достигает десятков миллионов, становится
актуальным вопрос ускорения трассировки лучей в таких рассеивающих структурах.
В случае распределения микроэлементов в узлах регулярной решетки вопрос ускорения решается просто. Однако если распределение микроэлементов
произвольно, то используется оптимальное бинарное разбиение пространства
микроэлементов. В соответствии с критерием (минимальное количество элементов с
каждой стороны) пространство делится на две части. Затем каждая часть опять
делится на две части, пока часть не будет содержать допустимое количество
микроэлементов или максимальная глубина дерева разбиений не будет достигнута.
При трассировке луч попадает в часть пространства, где он «видит» только те
элементы, которые находятся в данной области. При переходе в следующую область
соответствующим образом меняются список «видимых» элементов. Такой подход
позволяет эффективно реализовать трассировку луча в ОЭ.
Возможность построения и моделирования регулярных микроструктур
присутствует в ряде программ оптического моделирования. Например, ASAP,
LightTools и SPEOS в разной степени имеют эти возможности. Если ASAP имеют
весьма ограниченные возможности (ограниченное количество форм и распределений
микроэлементов) и низкую эффективность трассировки лучей, то LightTools и,
особенно, SPEOS позволяют построить практически любое распределение
микрогеометрических элементов произвольной формы [3, 10]. Однако основной
недостаток этих программ – малое количество независимых микроэлементов. SPEOS
допускает наличие только 3 млн. элементов, в то время как ОЭ, разработанные нами,
позволяют строить распределение из 30 млн. независимых микроэлементов. Кроме
того, SPECTER с ОЭ показал наивысшую эффективность моделирования (скорость
трассировки лучей), превысив на аналогичных оптических системах как минимум в
1.5 раза эффективность работы SPEOS (эффективность ASAP и LightTools
значительно ниже, чем SPEOS).
5. Пример моделирования и проектирования осветительной системы
жидкокристаллического дисплея
Интеграция ОЭ с поверхностным рассеиванием в систему SPECTER позволила
производить сквозное моделирование сложных систем подсветки
жидкокристаллических дисплеев, содержащих рассеивающие микроэлементы.
Используя новые возможности ОЭ с поверхностным рассеиванием, были успешно
спроектированы десятки реальных оптических систем подсветки
жидкокристаллических мониторов. Пример одной такой системы показан на рис. 7.

Рис. 7. Система подсветки жидкокристаллического дисплея
Оптическая система освещается четырьмя светодиодами, а вывод света из
светопроводящей пластины осуществляется микроэлементами, нанесенными на дно
пластины. Форма микроэлементов и область, где они расположены, показаны на рис.
8 и 9 соответственно.
Рис. 8. Форма микроэлементов.
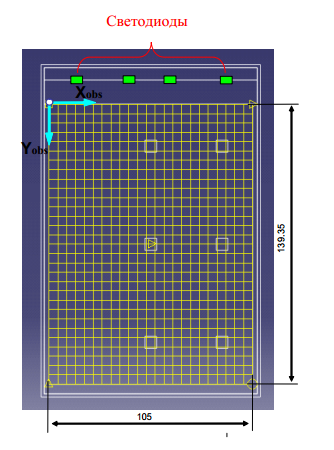
Рис. 9. Область определения микроэлементов.
8,5 миллионов микроэлементов одинаковой формы и размера было равномерно
распределены на дне светопроводящей пластины. Моделирование проводилось в
течение часа на компьютере P4-3200, 2Gb RAM. Достигнутая точность была 1.3%.
Результаты моделирования (распределения освещенности виртуального экрана,
расположенного над областью микроэлементов и вне пластины) показаны на рис. 10.
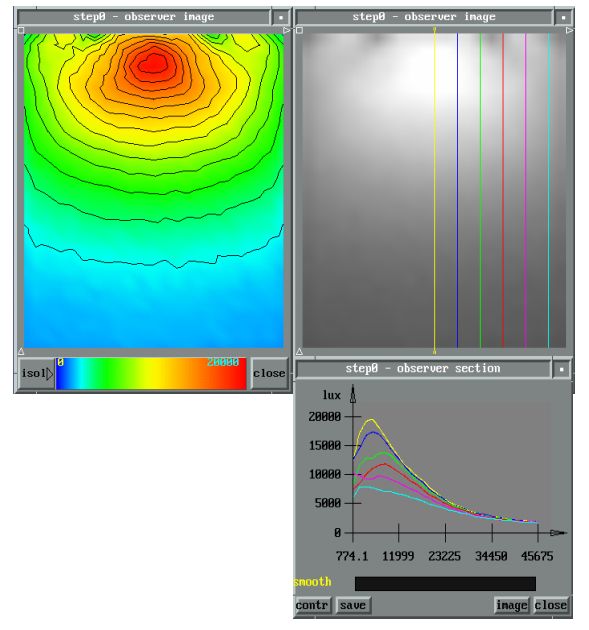
Рис. 10. Результаты моделирования.
Кроме того, было произведено проектирование оптической системы подсветки
жидкокристаллического дисплея. Целью проектирования было достижение
максимально равномерной яркости экрана. В качестве параметра оптимизации
использовался масштаб длины микроэлемента, показанный на рис. 11. Масштаб
длины является двумерной функцией, чьи аргументы – координаты положения
микроэлемента на поверхности светопроводящей пластины. То есть в каждой точке области распределения микроэлементов можно задать собственную длину
микроэлемента.

Рис. 11. Параметр оптимизации.
В процессе оптимизации было достигнуто равномерное распределение
выходной яркости. масштаб длины микроэлемента изменился кардинальным
образом. Результаты первого и последнего шага показаны на рис. 12.
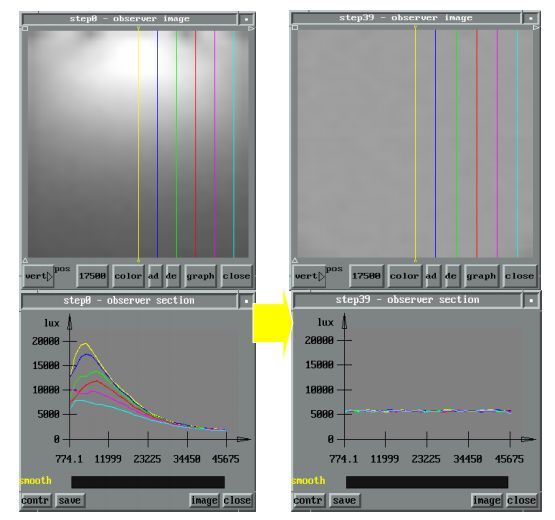
Рис. 12. Результаты расчета на первом и последнем шагах оптимизации.
Эти результаты обеспечиваются распределением масштаба длины
микроэлементов, показанным на рис. 13.
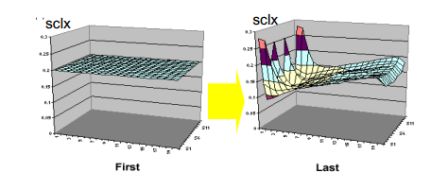
Рис. 13. Распределение масштаба длин элементов sclx на первом и последнем
шагах оптимизации
На первом шаге оптимизации длины всех микроэлементов были одинаковы
(что соответствует равномерному распределению микроэлементов). На последнем
шаге вариация длин достигает трех раз, что обеспечивает равномерную выходную
яркость.
6. Заключение
В работе рассмотрена концепция, реализация и интеграция ОЭ с
поверхностным рассеиванием в программную систему оптического моделирования
SPECTER. На реальном примере был проиллюстрирован процесс компьютерного
моделирования и проектирования системы подсветки жидкокристаллического
дисплея с использованием ОЭ с поверхностным рассеиванием.
Работа поддержана РФФИ, грант № 06-07-89162, а также компанией INTEGRA
Inc. (Япония).
Литература:
1. Волобой А.Г., Галактионов В.А., Машинная графика в задачах
автоматизированного проектирования. «Информационные технологии в
проектировании и производстве», № 1, 2006, стр. 64-73.
2. Breault Research Organization, http://www.breault.com/software/softwareoverview.php
3. Optical Research Associates, http://www.opticalres.com/lt/ltprodds_f.html
4. OPTIS, http://www.optis-world.com/G_O.asp?soft_id=1
5. 3D textures, SPEOS, OPTIS,
http://ntdd2110.fm.netbenefit.co.uk/WebData/3dtextures%20v2.pdf
6. Sergey Ershov, Dmitry Zhdanov. Efficient Application of Optical Objects in Light
Simulation Software. 15-th International Conference on Computer Graphics and Vision
GraphiCon-2005, Novosibirsk, June 21 - 24, 2005. Conference Proceedings p. 284-288.
7. SPECTER – Computer-Based Optical Modeling and Design System.
http://www.integra.jp/eng/products/specter/index.htm
8. A.Khodulev, E.Kopylov Physically accurate lighting simulation in computer
graphics software. Proc. GraphiCon’96 - The 6-th International Conference on Computer
Graphics and Visualization, St.Petersburg, 1996, p. 111-119.
9. А.Г. Волобой, В.А. Галактионов, К.А. Дмитриев, Э.А. Копылов.
Двунаправленная трассировка лучей для интегрирования освещенности методом
квази- Монте Карло. "Программирование", № 5, 2004, с. 25-34.
10. Optical Design Tools for Backlight Displays, LightTools, Optical Research
Associates, http://www.opticalres.com/white%20papers/ToolsforBacklights.pdf












