Àâòîðû: Aila T., Laine S.
Èñòî÷íèê: Aila T., Laine S. Understanding the efficiency of ray traversal on GPUs //Proceedings of the Conference on High Performance Graphics 2009. – ACM, 2009. – Ñ. 145-149. http://www.eng.utah.edu/~cs7940/papers09/Timo_GPU_rt_HPG09.pdf
We discuss the mapping of elementary ray tracing operations— acceleration structure traversal and primitive intersection—onto wide SIMD/SIMT machines. Our focus is on NVIDIA GPUs, but some of the observations should be valid for other wide machines as well. While several fast GPU tracing methods have been published, very little is actually understood about their performance. Nobody knows whether the methods are anywhere near the theoretically obtainable limits, and if not, what might be causing the discrepancy. We study this question by comparing the measurements against a simulator that tells the upper bound of performance for a given kernel. We observe that previously known methods are a factor of 1.5–2.5X off from theoretical optimum, and most of the gap is not explained by memory bandwidth, but rather by previously unidentified inefficiencies in hardware work distribution. We then propose a simple solution that significantly narrows the gap between simulation and measurement. This results in the fastest GPU ray tracer to date. We provide results for primary, ambient occlusion and diffuse interreflection rays.
CR Categories: I.3.3 [Computer Graphics]: Picture/Image Generation – [I.3.7]: Computer Graphics—Three-Dimensional Graphics and Realism
Keywords: Ray tracing, SIMT, SIMD
This paper analyzes what currently limits the performance of acceleration structure traversal and primitive intersection on GPUs. We refer to these two operations collectively as trace(). A major question in optimizing trace() on any platform is whether the performance is primarily limited by computation, memory bandwidth, or perhaps something else. While the answer may depend on various aspects, including the scene, acceleration structure, viewpoint, and ray load characteristics, we argue the situation is poorly understood on GPUs in almost all cases. We approach the problem by implementing optimized variants of some of the fastest GPU trace() kernels in CUDA [NVIDIA 2008], and compare the measured performance against a custom simulator that tells the upper bound of performance for that kernel on a particular NVIDIA GPU. The simulator will be discussed in Section 2.1. It turns out that the current kernels are a factor of 1.5–2.5 below the theoretical optimum, and that the primary culprit is hardware work distribution. We propose a simple solution for significantly narrowing the gap. We will then introduce the concept of speculative traversal, which is applicable beyond NVIDIA’s architecture. Finally we will discuss approaches that do not pay off today, but could improve performance on future architectures.
Scope This document focuses exclusively on the efficiency of trace() on GPUs. In particular we will not discuss shading, which may or may not be a major cost depending on the application. We will also not discuss the important task of building and maintaining acceleration structures.
Hierarchical traversal In a coherent setting, truly impressive performance improvements have been reported on CPUs using hierarchical traversal methods (e.g. [Reshetov et al. 2005; Wald et al. 2007]). These methods are particularly useful with coherent rays, e.g. primary, shadow, specular reflection, or spatially localized rays such as short ambient occlusion rays. It is not yet clear how beneficial those techniques can be on wide SIMT machines, or with incoherent rays such as diffuse or mildly glossy interreflection. We acknowledge that one should use hierarchical tracing methods whenever applicable, but this article will not cover that topic. Apart from special cases, even the hierarchical methods will revert to tracing individual rays near the leaf nodes. The awkward fact is that when using hierarchical tracing methods, only the most coherent part of the operations near the root gets accelerated, often leaving seriously incoherent per-ray workloads to be dealt with. This appears to be one reason why very few, if any, meaningful performance gains have been reported from hierarchical tracing on GPUs.
SIMT/SIMD SIMT is a superset of SIMD with execution divergence handling built into hardware. SIMT typically computes all control decisions, memory addresses, etc. separately on every (SIMD) lane [Lindholm et al. 2008]. The execution of trace() consists of an unpredictable sequence of node traversal and primitive intersection operations. This unpredictability can cause some penalties on CPUs too, but on wide SIMD/SIMT machines it is a major cause of inefficiency. For example, if a warp1 executes node traversal, all threads (in that warp) that want to perform primitive intersection are idle, and vice versa. We refer to the percentage of threads that perform computations as SIMD efficiency.
All of the tests in this paper use bounding volume hierarchy (BVH) and Woop’s unit triangle intersection test [Woop 2004]. The raybox and ray-triangle tests were optimized in CUDA 2.1 by examining the native assembly produced. The BVH was built using the greedy surface-area heuristic with maximum leaf node size 8 for all scenes. To improve tree quality, large triangles were temporarily split during the construction [Ernst and Greiner 2007]. The two BVH child nodes were stored in 64 bytes, and always fetched and tested together. The traversal always proceeds to the closer child. Woop’s intersection test requires 48 bytes per triangle. Further information about the scenes is given in Table 1. All measurements were done using an NVIDIA GTX285. Register count of the kernels ranged from 21 to 25 (this variation did not affect performance). We used a thread block size of 192, but most other choices were equally good. Rays were assigned to warps following the Morton order (aka Z-curve). All data was stored as array-ofstructures, and nodes were fetched through a 1D texture in order to benefit from the texture cache, while triangles were retrieved directly from global memory. This organization proved to have highest performance on GTX285, even though global memory accesses are not cached. As our primary focus is on simulated vs. measured performance, most of the results should not be overly sensitive to a particular data structure, intersection test, or tree constructor.
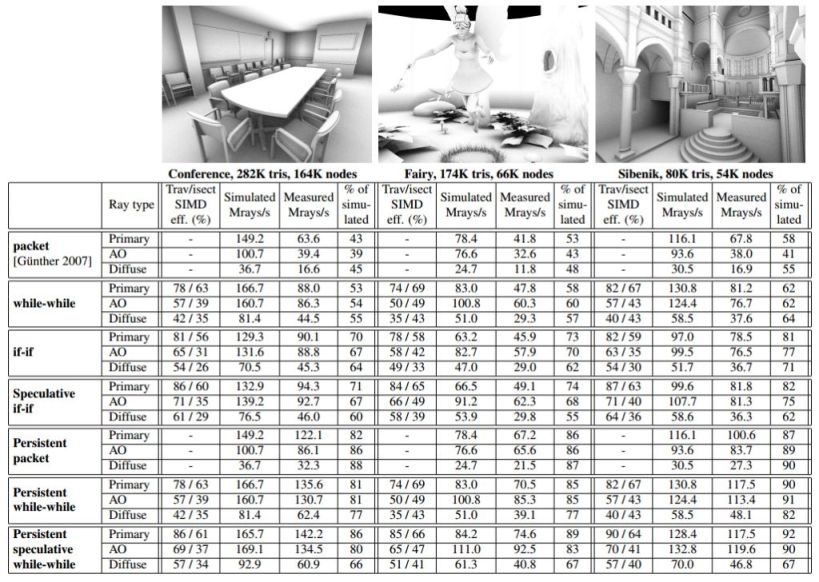
Table 1: Statistics from three static test scenes using several trace() methods. The performance numbers are averages from 5 representative viewpoints per scene. The screenshots show viewpoints that correspond roughly to the measured average performance in that scene. Output resolution was 1024x768 and the measurements were done using NVIDIA GTX285. The timings include only the time spent on tracing the rays. 32 ambient occlusion (AO) and diffuse interreflection rays were cast per pixel, distributed according to a Halton sequence on the hemisphere. Ambient occlusion rays were quite long, as depicted in the screenshots that were shaded using ambient occlusion only. Diffuse interreflection rays were very long and reported the closest intersection. The node counts include leaf nodes. SIMD efficiency is not reported for packet traversal because our implementation had all rays active even when they did not not intersect a particular node. This approach did not cause performance penalties as it neither increases memory bandwidth requirements nor causes the execution of additional instructions.
Our infrastructure does not support textures, which is apparent in the Fairy scene that should have more detail in the plant leaves. This of course distorts the absolute numbers a little bit but it does not affect the fairness of the comparison between the methods. The other two scenes do not have alpha textures.
We wrote a simulator that can estimate the upper bound of performance obtainable on an NVIDIA GPU or other wide SIMT machine. We dump the sequence of traversal, leaf, and triangle intersection operations required for each ray. We know, from native assembly code, the sequence of instructions that needs to be issued for each operation. Our simulator can then run the ray dump with a chosen ”scheduling” method and SIMD width, and report SIMD efficiency and estimated execution speed. The simulated performance includes the effect of SIMD efficiency, but we quote the efficiency numbers as well because they reveal additional information. We assume optimal dual issue rate on GTX285, meaning that every instruction that can theoretically execute in the secondary (SFU) pipe, does so [Lindholm et al. 2008]. Also, all memory accesses are assumed to return immediately. Consequently, GTX285 cannot, under any circumstances, execute the required instructions faster than the simulator, and therefore the simulator provides a hard upper bound for the performance. This upper bound is exactly what we want because it tells when a large chunk of performance is missing for some reason and whether the execution speed could be limited by memory-related issues.
Simulators that model the latencies of memory subsystem as well as the latency hiding capabilities of the processor cores have other important uses, especially in guiding decisions about future architectures, but those details are outside the scope of this paper.
In this section we study the simulated vs. measured performance of several trace() methods. These methods assign one ray to each thread unless stated otherwise.
In our terminology packet traversal means that a group of rays follows exactly the same path in the tree [Wald et al. 2001]. This is achieved by sharing the traversal stack among the rays in a warpsized packet, which implies rays will visit (potentially many) nodes they do not intersect but also that memory accesses are very coherent because each node is fetched only once per packet. We implemented and optimized the method of Gunther et al. [2007]. Our implementation uses the __any() voting primitive available in GTX285 [NVIDIA 2008] for faster traversal decision (instead of shared memory broadcasting).
Thanks to coherent memory accesses, one could reasonably believe that packet traversal would be close to the simulated optimal performance with at least coherent primary rays where few redundant nodes are visited. Therefore it is surprising that the measured numbers are a factor of 1.7–2.4 off from simulations, as shown in Table 1. One explanation could be that the performance is limited by memory bandwidth even with coherent rays. Alternatively, it could be that one simply cannot reach the full potential of the architecture in practice. We will investigate how other trace() methods behave while searching for the answer.
A simple alternative to packet traversal is to let each ray traverse independently, exactly to the nodes it actually intersects. A separate traversal stack needs to be maintained for each ray, and in our implementation the full per-ray stacks are stored in thread-local memory (external memory), following the outline of Zhou et al. [2008]. On SIMT processors that compute control decisions and addresses on every lane anyway (e.g. GTX285) this approach does not cause any additional computations. Its theoretical performance is always superior to packet traversal because rays do not visit nodes they do not intersect. However, it does lead to less coherent memory accesses. This per-ray method is typically implemented as follows:
We refer to this loop organization as ”while-while”. Because of less coherent memory accesses, one could expect the discrepancy between simulated and measured performance to be strictly larger for per-ray traversal than packet traversal, at least for primary rays for which packet traversal does not visit many extra nodes. However, Table 1 indicates the gap is actually smaller, contradicting the idea of memory bandwidth being a major issue. This conclusion is further strengthened by the observation that the less coherent ray types (ambient occlusion and diffuse) are not any further from the simulated numbers than primary rays, even though they should hit the memory bandwidth limits much sooner.
Interestingly, we see almost equal performance with the following loop organization, which should be about 20% slower according to simulations:
Measurements indicate this loop organization leads to even less coherent memory accesses, which should not affect performance favorably. Table 1 shows that the SIMD efficiency numbers are quite different in while-while and if-if, but the simulated numbers already include that, so it is not the explanation we are looking for. Nevertheless, the SIMD efficiency numbers are interesting because they clearly show if-if has better efficiency in traversal. By subdividing the acceleration structure more finely (e.g. max 4 tris per leaf), if-if can actually be much faster than while-while. But what favors if-if even in cases where it is theoretically inferior?
Additional simulations revealed that if-if leads to fewer exceptionally long-running warps. The distributions of warp execution times of while-while and if-if are otherwise similar, but the slowest warps are about 30% faster in if-if. For this to improve performance, some of the cores would have to be underutilized due to reasons related to varying execution time. To understand how this could happen, we must take a look into how the work is distributed inside the GPU.
All NVIDIA’s currently available cards (GeForce, Quadro, and Tesla brands) have CUDA work distribution units that are optimized for homogeneous units of work. For a wide variety of applications this is reasonable, and excellent results have been reported. Unfortunately, in ray tracing the execution time of individual rays vary wildly, and that may cause starvation issues in work distribution when long-running rays or warps keep distribution slots hostage.
In order to study whether work distribution is a significant factor in efficiency of trace() kernels, we need to bypass the units. This is easily achieved by launching only enough threads to fill the machine once. These long-running persistent threads can then fetch work from a global pool using an atomic counter until the pool is empty. As long as the atomic counter does not cause significant serialization, underutilization will not occur with this design.
We implemented persistent variants of the packet traversal and while-while. As shown in Table 1, the packet traversal got 1.5–2.2 times faster, and its performance is now within 10–20% of the theoretical upper bound for all ray types. One cannot reasonably hope to get much closer to the theoretical optimum because that would imply, among other things, optimal dual issue, complete absence of hardware resource conflicts, all memory access latencies to be hidden, and all of our>20K concurrent threads to terminate exactly at the same time.
The persistent while-while shows remarkably similar development, which implies its performance cannot be significantly limited by the memory bandwidth either. It is worth noticing that while-while is faster than packet traversal in all cases, and with diffuse rays the difference is approximately 2X.
The implementation of persistent threads is given in Appendix A.
The idea behind speculative traversal is simple: if a warp is going to execute node traversal anyway, why not let all the rays participate? It may be that some rays have already found triangles they would like to test intersections with before (possibly) switching back to traversal, but if they don’t execute node traversal, they’re idle. Therefore it can be beneficial to execute traversal for all rays. It may of course happen that the remaining triangle tests would have terminated a ray, and no further traversal would have been necessary. In that case the only extra cost is the memory bandwidth and latency needed for fetching the (unnecessary) node data. By definition this does not cause redundant computation on SIMD/SIMT because the code would have been executed anyway. Speculative traversal is theoretically beneficial because it improves the SIMD efficiency of traversal. It should improve the performance whenever the speed of memory subsystem is not limiting the execution speed.
The maximum number of postponed leaf nodes is an important practical consideration. Traditional traversal corresponds to a postpone buffer size of zero. We currently use a single-entry buffer in order to balance between overfetch, implementation simplicity, and SIMD efficiency improvement. In some scenarios it may be beneficial to use a larger postpone buffer.
Table 1 has results for speculative traversal variants of if-if and persistent while-while kernels. In accordance with expectations, the performance of primary rays improves up to 5% (SIMD efficiency of traversal is already high) and ambient occlusion gets up to 10% faster. However, diffuse rays fail to get any faster on the average, contradicting the simulation results, which suggests the redundant node fetches start to hurt the performance. This is the first clear sign of trace() being limited by memory bandwidth.
In this section we briefly discuss several possibilities for improving the SIMD efficiency and performance further. These methods do not currently pay off on GTX285, but simulations suggest some of them could be beneficial if a few new instructions were introduced.
It often happens that a few long-running rays keep the entire warp hostage. We modified the persistent threads approach to periodically replace the terminated rays with new ones that start from the root. This approach clearly improves the SIMD efficiency, but it also leads to less coherent memory accesses and causes computational overhead. An important detail is that one should avoid the while-while loop organization here because the new rays tend to visit many nodes before they find first primitives to intersect. Better SIMD efficiency and performance can be obtained by limiting the while loops to max N iterations, we used N = 4.
Both simulations and practical measurements confirm that occasional performance gains are possible by replacing terminated rays, but it also hurts in cases where the SIMD efficiency is already high (primary rays). We tried to fetch new data every n mainloop iterations and to limit the fetching to situations where at least m rays had terminated, but no parameter values were found that yielded consistent performance improvements on GTX285. In some individual viewpoints ambient occlusion rays got almost 10% faster, but overall the idea does not currently seem worth additional tunable parameters.
The computational overhead of this approach could be halved by introducing two new warp-wide instructions. Prefix sum [Blelloch 1990] enumerates the threads (inside a warp) for which a condition is true and returns a unique index [0; M1] to those threads. Population count returns the number of threads for which a condition is true, i.e.M above. These two instructions allow fast parallel fetching of new rays. Simulations suggest that ambient occlusion and diffuse rays could benefit up to 20%, assuming infinitely fast memory. Alas, diffuse rays are already limited by the speed of memory, and for these gains to materialize future devices would need to have faster memory compared to computational power.
5.2 Work queues
Work queues offer a simple way of guaranteeing almost perfect SIMD utilization regardless of SIMD width or ray load. If our warp width is 32 and we maintain at least 63 rays, then, by pigeonhole principle, there must be at least 32 rays that want to execute either traversal or intersection. In practice we maintain 64 rays, and the 32 extra rays are kept in an on-chip array (”shared” in CUDA).
The challenge is to shuffle the rays quickly between registers and shared memory. The shuffling consists of several operations. First we need to count the traversal and intersection populations among the 64 rays. Then we select the operation that has greater support, use prefix sums to compute the SIMD lanes and shared memory locations for rays, and finally shuffle the rays and corresponding states to correct locations. This process is quite expensive without population count and prefix sum instructions, and very slow on GTX285 in practice. If the two instructions existed, the ideal cost should be approximately 10 instructions for coordination and 2x10 instructions for moving the rays around, assuming a ray and its state fit into ten 32-bit registers. In our implementation the ray takes six registers (origin, direction) and a state consists of a stack pointer, current node pointer, ray id, and current closest intersection distance. The contents of traversal stacks are in external memory and do not need to be swapped.
We simulated the theoretical effectiveness of this approach with ambient occlusion and diffuse rays of the Fairy scene. This example was chosen because it has the lowest SIMD utilization in Table 1. The simulation used a modified while-while with the following parameters: replace all terminated rays every 4 mainloop iterations, limit traversal and intersection while loops to max 4 iterations (see Section 5.1), cost of shuffling 30 instructions, cost of fetching and initializing new rays 50 instructions. The simulated performance was 137.9 Mrays at SIMD efficiency of 85/84 for ambient occlusion, and 92.1 Mrays at 85/85 efficiency for diffuse. These correspond to roughly 40% and 80% performance improvements, respectively. Closer to 100% efficiency, but lower simulated performance, was achieved by limiting the while loops to 1 or 2 iterations. More frequent fetching of new rays increased the efficiency slightly but resulted in a net loss due to the computational overhead.
There are so many assumptions built into these numbers that firm conclusions cannot be made yet, but it seems likely that work queues could be beneficial in cases where the primary bottleneck is low SIMD efficiency.
Trees with branching factor higher than two can make memory fetches more coherent and possibly improve the SIMD efficiency, and may therefore improve performance on some platforms. We implemented a kernel that supported branching factors 4, 8, 16 and 32, by assigning a ray to the respective number of adjacent threads. Our implementation was significantly slower than binary trees in all of our test cases. The effect was particularly clear with trees wider than four. It seems likely, however, that our implementation was not as efficient as the one described by Wald et al. [2008], because GTX285 does not have the prefix sum (compaction) instruction.
There are several challenges with this approach. Wide trees replicate some computations to multiple SIMT lanes and add a certain amount of inter-thread communication. Also, trees wider than 4 tend to perform many more ray-node tests than traditional binary trees, leading to additional memory fetches and redundant computations compared to per-ray kernels. A further limitation is that tree types that encode partial nodes (e.g. KD-trees, BIH [Wachter and Keller 2006]) cannot be easily used.
We have shown that the performance of fastest GPU trace() kernels can be improved significantly by relying on persistent threads instead of the hardware work distribution mechanisms. The resulting level of performance is encouraging, and most importantly the less coherent ray loads are not much slower than primary rays. It seems likely that other tasks that have heterogeneous workloads would benefit from a similar solution.
In additional tests we noticed that in these relatively simple scenes the performance of our fastest speculative kernel remains around 20–40Mrays/sec even with randomly shuffled global illumination rays. These ray loads are much less coherent than one could expect from path tracing, for example, so it seems certain that we would be able to sustain at least that level of performance in unbiased global illumination computations.
We have also shown that, contrary to conventional wisdom, ray tracing performance of GTX285 is not significantly hampered by the lack of cache hierarchy. In fact, we can also expect good scaling to more complex scenes as a result of not relying on caches. However, we do see the first signs of memory-related effects in the fastest speculative while-while kernel in diffuse interreflection rays. In these cases a large cache could help.
Additional simulations suggest that a 16-wide machine with identical computational power could be about 6–19% faster than 32- wide in these scenes, assuming infinitely fast memory. The difference was smallest in primary rays and largest in diffuse, and it also depended on the algorithm (min/average/max (%)): whilewhile (9/14/19), speculative while-while (6/10/15), if-if (8/10/13), speculative if-if (6/8/12). This suggests that speculative traversal is increasingly useful on wider machines. Theoretically a scalar machine with identical computational power could be about 30% (primary) to 144% (diffuse) faster than 32-wide SIMD with the used data structures, again assuming infinitely fast memory.
Acknowledgements Marko Dabrovic (www.rna.hr) for the Sibenik cathedral model. University of Utah for the Fairy scene.