Автор: Мазовка Д.И.
Источник: Мазовка Д. И. Формальный подход к решению задачи визуализации. – 2011. http://elib.bsu.by/bitstream/123456789/9851/1/41%20%D0%9C%D0%90%D0%97%D0%9E%D0%92%D0%9A%D0%90.pdf
В работе предлагается подход к решению проблемы разработки графических систем, основанный на специализированной алгебре визуализации. Представленная методология позволяет снизить затраты на разработку и поддержку систем визуализации для широкого класса задач.
Ключевые слова: графический конвейер, визуализация, алгебра визуализации, графические системы.
При решении прикладных задач часто возникает необходимость в визуальном представлении полученных результатов. В связи с этим появилось новое научное направление – компьютерная графика. В процессе своего развития сформировался особый ее тренд, определив концепцию графического конвейера. Это совокупность подходов, алгоритмов, устройств и программ, реализующих процесс визуализации – перевод данных из исходного представления в двумерное изображение.
Развитие графического конвейера шло по пути максимальной автоматизации его функций. Значительная часть алгоритмического наполнения реализовалось аппаратными средствами, а программный интерфейс был вынесен в соответствующие аппаратно-независимые библиотеки [1]. Вместе с тем при разработке реальных систем визуализации возникает множество стандартных проблем и подзадач, которые можно позиционировать между автоматизированной частью конвейера и исходной прикладной задачей, образуя своеобразный промежуточный программный уровень.
В работе предлагается подход, в котором, определяя дополнительный уровень абстракции в виде универсальной задачи визуализации, задается потенциальное направление для дальнейшей автоматизации функционального наполнения графического конвейера.
Рассмотрим базовые понятия компьютерной графики. Вначале определим, что такое компьютерная графика.
Компьютерная графика (также машинная графика) – это область деятельности, в которой компьютеры используются как для синтеза (создания) изображений, так и для обработки визуальной информации, полученной из реального мира. Также компьютерной графикой называют результат такой деятельности [2].
Визуализация в общем смысле – это процесс или результат представления информации. В компьютерной графике процесс визуализации определяется специальным термином – рендеринг (rendering). В данном контексте под этим термином понимается набор аппаратно-программных средств, реализующих процесс генерации изображения. Можно выделить два основных подхода, реализующих процесс рендеринга – растеризацию (rasterization) и группа методов, реализующих глобальное освещение (трассировка лучей (raytracing), радиосити (radiosity), ambient occlusion).
Растеризация – это метод рендеринга, реализующий отображение трехмерных векторных данных в двумерные кадры. При растеризации представление реальности достигается не моделированием, а имитацией или приближением реальных процессов. Это позволяет значительно ускорить время генерации изображений в отличие от методов глобального освещения.
В силу высокой вычислительной трудоемкости методы глобального освещения не использовались при динамическом рендеринге. Но благодаря возможностям современного аппаратного обеспечения, это ограничение постепенно снимается. Тем не менее графическое оборудование в большей степени использует именно методы растеризации.
Процесс растеризации в рендеринге можно представить в виде так называемого графического конвейера. Технология конвейера появилась в середине 1990-х гг., когда были созданы первые видеоускорители, автоматизирующие некоторые операции растеризации. В настоящее время конвейер представлен широким набором постоянно совершенствующихся средств. В общем виде конвейер можно представить в виде этапов [2]:
Проблема повышения производительности конвейера на разных этапах решается по-разному. На аппаратном уровне это решается в основном путем наращивания количества обрабатывающих процессоров, повышая при этом объемы и качество памяти. На программном уровне, из-за слабой формализации процесса визуализации, существуют определенные проблемы. В силу наличия большого количества разнообразных прикладных задач визуализации, а также отсутствия универсальной методологии их решения появляется узкое место. Разработчикам предлагаются два варианта:
В первом случае в процессе решения задачи неизбежно появятся искажения, обусловленные особенностями и ограничениями применяемой системы. Расширение первоначальной задачи также ставится под вопрос, так как в этом случае может понадобиться существенная переработка используемой системы, либо отказ от нее в пользу какой-либо другой.
Во втором случае решение заведомо трудоемко и затратно.
Одним из путей решения проблемы может стать стандартизация этого процесса.
Ниже предлагается подход, основанный на алгебре визуализации – языке формального описания процесса визуализации.
Процесс визуализации можно представить в виде выражения: Model -> Frames, где Model — это визуализируемая математическая модель некоторого реального явления, а Frames — последовательность кадров, визуализирующая динамику изменений модели. С учетом обобщенных этапов графического конвейера, выражение представляется в виде: Model -> HAL -> HW -> Frames, где HAL (Hardware Abstraction Layer) – интерфейс графического оборудования HW (Hardware).
Переход от модели к интерфейсу оборудования является интересующей нас областью. Проблема состоит в том, что в общем случае модель может описываться произвольным образом, в то время как с другой стороны требуется получить в ее стандартном представлении в виде последовательности инструкций, понятных оставшейся части конвейера [3]. Это преобразование можно изобразить с помощью рис. 1:
Рисунок 2 – Процесс визуализации
Переход от модели к последовательности инструкций осуществляется через множество преобразований и упорядочивание данных. Этот процесс может быть представлен в виде графа, узлами которого являются процедуры трансформации данных. Для формального описания этой структуры предлагается специализированная алгебра визуализации.
Алгебра визуализации – это система, состоящая из множества объектов и опе- раций визуализации, а также правил применения этих операций к объектам. В число объектов алгебры входят:
В качестве операций алгебры введем следующие четыре:
Классом назовем именованную совокупность объектов, имеющих определенный набор атрибутов, а также заданные ограничения значений этих атрибутов. Множества объектов разных классов в то же время могут пересекаться.
Определение операции выборки (A, B — множества объектов) (рис. 2):
Рисунок 2 – Определения операций выборок
Задача визуализации звучит следующим образом:
Имея сцену S, построить визуализацию в виде кадра F.
Переформулируя ее в терминах алгебры визуализации, получим:
Имея сцену S, построить операторное выражение R определенное в алгебре визуализации, генерирующее кадр F: R(S) = F.
Операторное выражение R представляет собой суперпозицию операций алгебры примененных к начальной сцене, и может быть интерпретировано в виде графа процесса визуализации (рис. 3):
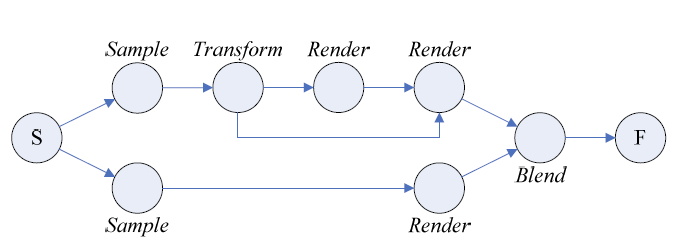
Рисунок 3 – Пример графа процесса визуализации
Таким образом, выражение образует ориентированный ациклический слабо связанный граф. В графе присутствует единственная начальная вершина S, недостижимая из любой другой вершины, но любая другая вершина достижима из S, а также единственная конечная вершина F, достижимая из любой другой вершины, но любая другая вершина недостижима из F.
Операции рендеринга и блендинга в алгебре генерируют конечные последовательности инструкций для оборудования, таким образом граф можно спроецировать на линейную последовательность команд (рис. 4). В итоге с помощью алгебры визуализации мы получаем формальное описание первого этапа работы графического конвейера для некоторой задачи визуализации.
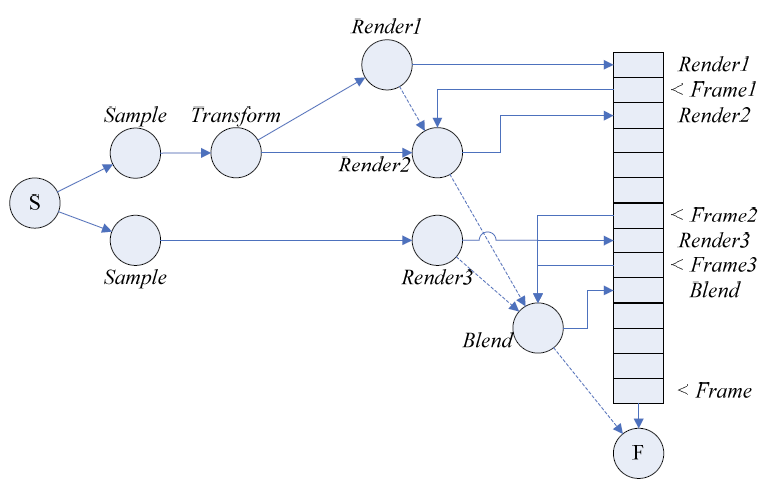
Рисунок 4 – Проецирование графа процесса на последовательность инструкций
Таким образом, введение формального описания процесса визуализации с помощью алгебры визуализации помогает стандартизировать методы решения типичных проблем, возникающих при разработке графических систем.
По аналогии с реляционной алгеброй и языками запросов, технической реализацией предложенного подхода может являться специализированный язык описания и построения процессов динамической визуализации. Это позволит удешевить создание и поддержку графических систем для различных прикладных задач.
В работе рассмотрена проблема организации систем визуализации реального времени. Предложен подход, связанный с формализацией процесса построения кадров в виде алгебры визуализации, которая является универсальным интерфейсом для разработки систем (по аналогии с реляционной алгеброй СУБД).